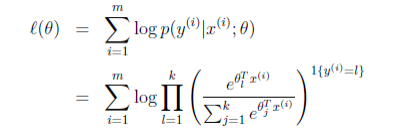深夜博客在今天开张啦
一年前接触了机器学习，纯属个人兴趣，还没想到要入坑，现在沉迷无法自拔了哈哈哈。好了也不说太多废话了，今天的主题是广义线性模型啦！这篇博客是参考斯坦福cs229 lecture1中的Generalize Linear Models（GLM）及加上自己的理解，博主是个new comer，欢迎大家一起交流学习哦
在解释广义线性模型之前，有必要回顾一下线性回归(Linear Regression)和逻辑回归(Logistic Regression)。

线性回归–Linear Regression
线性回归模型可应用与监督学习(supervised learning)预测问题，如房价预测，疾病预测…….
对线性回归的直观解释: 找到一个线性函数能尽可能拟合已给出的点，如图

理论解释：
假设

$$X=[x_1,x_2,x_3,.......,x_m]T$$ $x_i$代表影响结果的一个特征(feature), y ∈ R
当X与结果y属于线性关系时，即可得到线性回归假设(hypotheses)：
$$h_θ(X) = θ_1x_1+θ_2x_2+.......+θ_mx_m+b；$$
写成向量形式即为：
$$h_Θ(X) = Θ^TX + b$$

构造损失函数（损失函数就是用来表现预测与实际数据的差距程度）:
cost function（损失函数）:

$$J(Θ) = 1/2\sum_{i}^{samples} { [h_Θ(X) - y]};$$
目标即找到一组 $Θ = [θ_1,θ_2,....,θ_m]$ 最小化J(Θ)。所用到的方法是梯度下降（gradient descent）,在这里就不具体展开了，详细请看机器学习之梯度下降
在得到Θ向量后，将X_predict代入 $h_Θ(X) = Θ^TX$ 中即可得到y_predict
Tips: 为什么要用最小二乘法定义损失函数, 戳=> 线性模型概率解释

逻辑回归–Logistic Regression
逻辑回归模型应用于监督学习分类问题，暂且考虑二分类(如0,1分类)问题如
直观解释：得到一条函数将不同类别的分开，如图:

理论解释:
同样假设

$$X=[x_1,x_2,x_3,.......,x_m],\\ Θ = [θ_1, θ_2, θ_3,.......θ_m]$$
定义hypotheses(也就是预测预测结果 $\hat{y}$) $$h_Θ(X) = 1/1+exp(-Θ^TX)\\ \left\{ \begin{array}{c} h_Θ(X) > 0.5, & \text{set $h_Θ(X)$ = 1}\\ h_Θ(X) < 0.5, & \text{set $h_Θ(X)$ = 0} \end{array} \right.$$
cost function:
$$J(Θ) =\begin{cases}-log(h_Θ(x^i)), & \text{if $y^i$ = 1} \\-log(1-h_Θ(x^i)), & \text{if $y^i$ = 0} \end{cases}$$
统一起来即为:
$$J(Θ) = -\sum_{i}^{samples} {[y^i log(h_Θ(x^i))+((1-y^i)log(1-h_θ(x^i))]}$$
同样是用到了梯度下降优化参数，得到优化后的参数 $Θ=[θ_1, θ_2, ……,θ_m]$后，X_predict代入 $h_Θ(X)$ 即可得到该X对应的分类

OK,线性回归和逻辑回归就到此为止了，以上都是直接给出了hypothesis的定义，那么问题就来了，怎么知道那是正确的呢，换句话说，对一个陌生的模型，怎么去定义它的hypothesis？
问题不是很严重，广义线性模型解决了这个问题！

广义线性模型
实际上这两种情况只是广义线性模型的特殊情况，接下来我将解释其他的广义线性家族模型是怎么推到和应用到回归和分类问题中！
对于线性回归和逻辑回归实际上都可以看作是一个(y|X; Θ)的问题 (Tips：“;”表示参数Θ已知)
//对(y|X;Θ)的解释: 在参数Θ固定，给定x情况下，y服从某种概率分布
不同的是：
1. 线性回归中， (y|x;Θ) ∼ $N(µ,σ^2)$,
2. 逻辑回归中， (y|x;Θ) ∼ Bernoulli(Φ),
高斯分布，伯努利分布的爸爸是同个人，他的名字叫指数族分布，现在我们就来介绍这个人并看看到底是如何生出演变成高斯分布和伯努利分布的！

指数族分布(Exponential Family)
指数族分布即为广义线性模型的概率分布
指数家族分布可定义为：

$$p(y;η) = b(y)exp(η^T T(y)−a(η))$$
其中:
1. η被称为自然参数(natural parameters)
2. 通常T(y) = y
通过不同的a(η) 和 b(y) , T(y)可将指数家族分布变成不同的概率分布

重点内容
广义线性模型的构造：
引用斯坦福cs229讲义上的原话：
1. y | x;θ ∼ ExponentialFamily(η). I.e., given x and θ, the distribution of y follows some exponential family distribution, with parameter η.
2. Given x, our goal is to predict the expected value of T(y) given x. In most of our examples, we will have T(y) = y, so this means we would like the prediction h(x) output by our learned hypothesis h to satisfy h(x) = E[y|x]. (Note that this assumption is satisfied in the choices for hθ(x) for both logistic regression and linear regression. For instance, in logistic regression, we had hθ(x) = p(y = 1|x;θ) = 0·p(y = 0|x;θ) + 1·p(y = 1|x;θ) = E[y|x;θ].)
3. The natural parameter η and the inputs x are related linearly: $η = θ^Tx$. (Or, if η is vector-valued, then $η_i = θ_i^Tx$.)

也就是说，GLM有三个假设:
一: 给定θ和x，(y|x;θ)服从以η为参数的指数族分布;
二. hypothesis $h_Θ(X) = E[y|x; Θ]$, 即为该分布的期望值
三. η与X是线性关系, $η = θ^TX$;当且仅当η是向量时，才有$η_i = θ_i^Tx$！

线性模型的推导(演变成高斯分布):
线性模型中目标变量y(response variable)是连续的，由机器学习线性回归概率解释中可以得到结论:y给定x服从高斯分布 N(µ,σ2),在这里μ可能由x决定；因此我们让指数家族分布设为高斯分布，演算以上广义线性模型构造：

比较目标概率分布函数与指数家族函数，确定参数之间的关系:
因为(y|X ; θ)~ExpFamily(η)~$N(μ, σ^2)$ 由高斯分布函数可得:

$$p(y; μ) = \frac {1} {\sqrt{2\pi}}exp(-(y-μ)^2/2)\\\implies \frac {1} {\sqrt{2\pi}}exp(-y^2/2 + μy - μ^2/2)\\\implies \frac {1} {\sqrt{2\pi}}exp(-y^2/2 )exp(μy - μ^2/2)$$
与指数分布族函数 $P(y;η) = b(y)exp(η^T T(y) - a(y))$对比可得
$$\left\{ \begin{array}{c}\color{red}{η = μ}\\b(y) = \frac {1} {\sqrt{2\pi}}exp(-y^2/2)\\a(y) = -μ^2/2\\T(y) = y\\\end{array}\right.$$
构造模型：
由于对于服从 $(μ, σ^2)$的高斯分布，其均值为μ,因此有:
$$h_Θ(X) = E[(y|X ; μ)] = μ$$

由以上推理得 $η = μ$, 所以有:

$$h_Θ(X) = E[(y|X ; μ)] = μ = η\\η = Θ^TX\\hθ(X) = θ^TX$$
这也正是以上线性回归hypothesis得到的结果，what a surprise!

逻辑回归模型的推导(演变成伯努利分布):
目标概率函数和指数家族函数之间的参数关系:
Logistic Regression二分类服从伯努利(Bernoulli)分布，表示为：
(y|X; θ)~ExpFamily(η)~Bernoulli(Φ)， Φ = p(y=1|x;θ)

$$p(y; Φ) = Φ^y(1-Φ)^{1-y} , \ y∈{0,1}\\\implies exp(log(Φ^y(1-Φ)^{1-y} )) = exp(logΦ^y + log(1-Φ)^{1-y})\\\implies exp(ylogΦ + (1-y)log(1-Φ)) = exp(ylogΦ + log(1-Φ) - ylog(1-Φ))\\\implies exp(ylog\frac {Φ} {1-Φ} + log(1-Φ))$$
与指数分布族函数 $P(y;η) = b(y)exp(η^T T(y) - a(y))$对比可得
$$\left\{ \begin{array}{c}T(y) = y\\b(y) = 1\\\color{red}{η = log \frac {Φ} {1-Φ} \implies Φ =\frac {1} {1+exp(-η)}} \\a(y) = log(1-Φ)\end{array}\right.$$
构造模型:
由于服从(Φ)的伯努利分布函数均值为Φ，得:
$$h_Θ(X) = E[(y|X ; Θ)] = E[(y; Φ)] = Φ$$
由以上推理得 Φ = 1/(1 + exp(−η)), 所以有:
$$h_Θ(X) = E[(y|X ; θ)] = 1/(1 + exp(-η))\\η = θ^TX\\h_Θ(X) = 1/(1 + exp(−Θ^TX))$$
正是logistic regression的hypothesis表达式，是不是很激动！！！

Tips: 定义以自然参数η作为概率分布均值的参数为g(η) = E[(y|X ; Θ)] = E[T(y); Θ]称为 canonical response function（规范响应函数，g(η)的逆函数则称为canonical link function(规范连接函数)；

重点内容
总结一下广义线性模型吧：
广义线性模型的核心体现在y服从指数族分布(包括高斯分布，伯努利分布，多项式分布，泊松分布，beta分布……)，且同个样本的y必须服从同个分布，接着在具体分布中比较与指数分布族之间的参数关系，最重要的就是具体分布的参数(Φ)和指数分布参数(η)之间的关系;
例如在线性回归中，Φ = η; 在逻辑回归中，Φ = 1/(1 + exp(−η))；找到了这个关系后则可构造模型: 求得具体分布的均值，用η代替Φ，再用$Θ^TX$代替η，即可求得具体模型的hypothesis($\hat{y}$)
在求得hypothesis后，求参数Θ利用极大似然估计求得cost function(损失函数)(具体方法参见机器学习之概率解释)，之后再用梯度下降优化参数Θ即可得到最优解!

Tips:
·通常情况下，T(y) = y;但当y有多个取值时(c>2),则T(y)也应该是c-1的向量;(c为y的维度)
·$η = Θ^TX$,但当η是向量时，有η_i = θ_i^TX$也就是具体分布有多个参数时(如多项式分布)！
以上两种情况在多分类问题softmax中出现，具体参见机器学习多分类softmax

鸡汤终于煲的差不多了，有什么不足的希望大神指点出来，还想熬更好喝的鸡汤哈哈

                                            2018-09-04 23：24