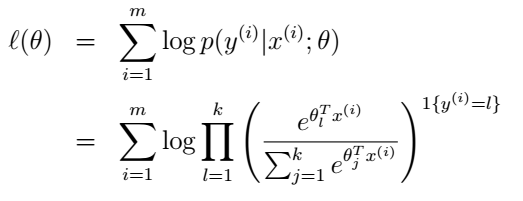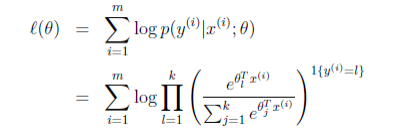---

当通过一系列连续型和/或类别型预测变量来预测二值型结果变量时，Logistic回归是一个非常有用的工具。

Logistic回归模型和我们熟知的多元线性回归模型有很多类似之处，下面就从多元线性回归模型来进行展开。

一、引入：多元线性回归模型

回归分析（regression analysis）是研究一个随机变量与一个（一元）或多个（多元）普通变量之间相关关系的一种常用的数理统计方法。这里普通变量是指其值可以控制或精确测定的那些变量，它可以是随机的，也可以是非随机的。

如何表达这种变量之间的相关关系呢？以一元回归为例：
由于因变量 Y 是随机变量，自变量 X 是普通变量，对于 X 的每一确定值，对应的 Y 有它的概率分布，即当 X=x0 时，依不同概率对应着 Y 的不同值，但所对应的Y的数学期望 y_hat 是一个确定的数。因此反映一个随机变量与一个普通变量的相关关系的方程y是随机变量Y的数学期望 y_hat=f(x) 随普通变量X变化而变化的一个函数关系式，称为回归方程，如果这个函数关系是线性的，即 y_hat=beta0+beta1x 就称为一元线性回归方程。
同理可得多元线性回归方程为:

在建立多元线性回归模型时，所选用的方法和步骤中，为使模型的回归效果显著，实际上作了如下几条假定：

• 假定1 线性假定：假定了变量之间的相关关系符合多元线性回归，即采用了线性模型

• 假定2 假定因变量y服从正态分布，即对一切i=1，2，…，n，yi服从正态分布，或等价的为εi服从正态分布
• 假定3 假定各项观察是独立的，即y1，y2，…，yn相互独立，或等价的有ε1，ε2，…，εn相互独立
• 假定4 假定方差齐性，即假定对一切i=1，2，…，n，yi的方差为常数，或等价的有εi的方差为常数

为此，在求线性回归方程时，需要对实际问题和数据进行考察，诊断上述假定是否成立，若不成立，就该有针对性的改进措施。

二、Logistic回归模型

上述多元线性回归模型要求因变量是连续型正态变量，且自变量与因变量之间呈线性关系等，这使它的应用受到限制。

当因变量是分类变量，且自变量与因变量没有线性关系时，则可以使用Logistic回归模型。它非常巧妙地避开了分类变量的分布问题，可完善地解决一大批实际应用问题。

那么应该怎样解决这个问题呢？研究者将所研究的问题转换一个角度，不是直接分析y与x的关系，而是分析y取某个值的概率P与x的关系。

例如，令y为1和0变量，y=1表示有病，y=0表示未患病；x是与患病有关的危险因素。如果P表示患病的概率，即P=prob（y=1），那么研究患病的概率P与危险因素x的关系就不是很困难的事情了。

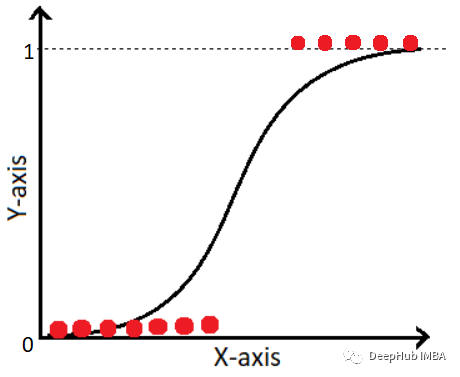
分析因变量y取某个值的概率P与自变量x的关系，就是寻找一个连续函数，使得当x变化时，它对应的函数值P不超出[0，1]范围。数学上这样的函数是存在且不唯一的，Logistic回归模型就是满足这种要求的函数之一。与线性回归分析相似，Logistic回归分析的基本原理就是利用一组数据拟合一个Logistic回归模型，然后借助这个模型揭示总体中若干个自变量与一个因变量取某个值的概率之间的关系。具体地说，Logistic回归分析可以从统计意义上估计出在其他自变量固定不变的情况下，每个自变量对因变量取某个值的概率的数值影响的大小。

Logistic回归模型有条件与非条件之分，前者适用于配对病例对照资料的分析，后者适用于队列研究或非配对的病例——对照研究成组资料的分析。

三、非条件logistic回归模型

（一）介绍

上述是数学上的Logistic曲线，因此，将此式描述的P与协变量间的回归关系称为线性Logistic回归。

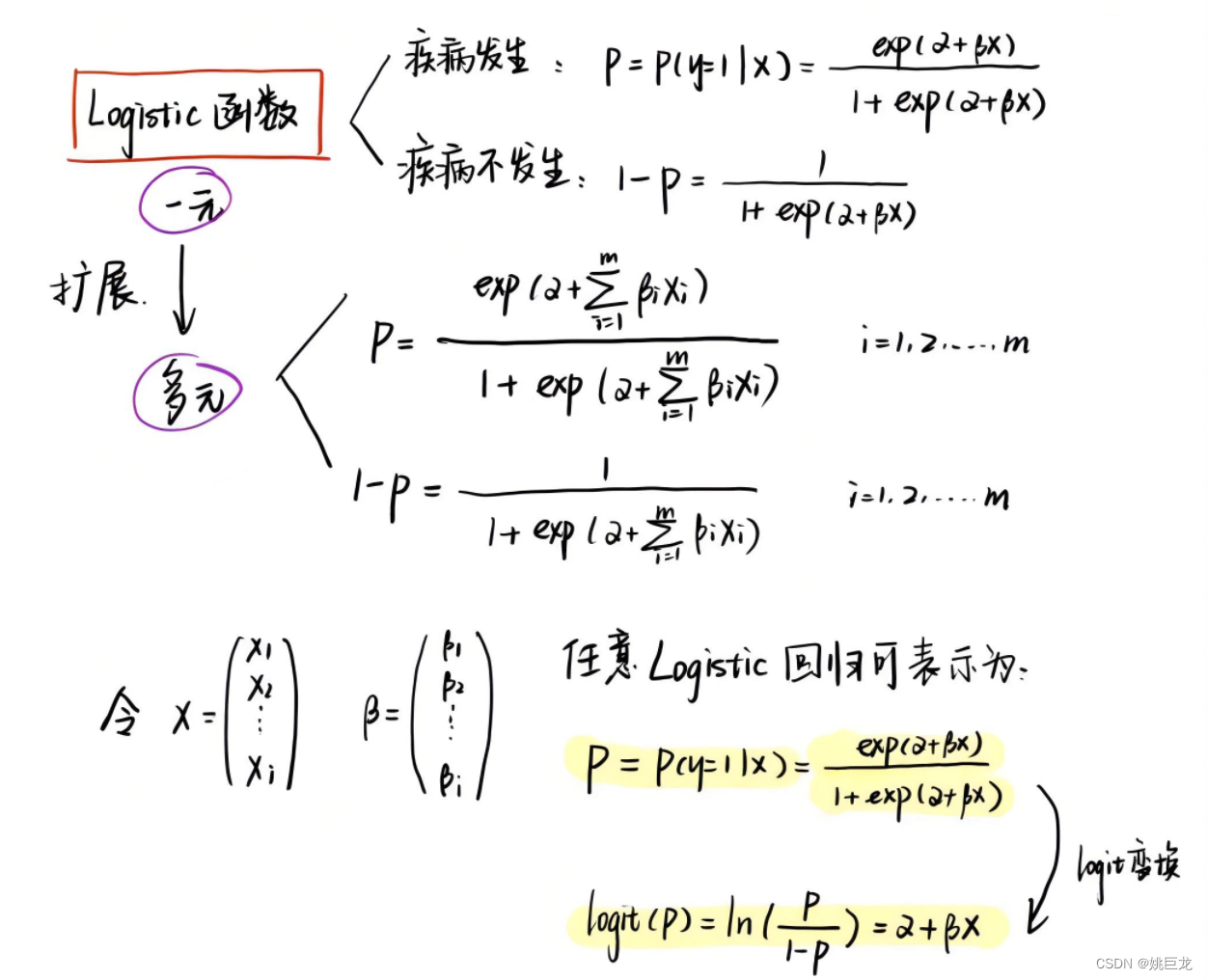
上述式子给出的是变量z=logit( P) 关于x的线性函数，而式子变换前给出的是变量P关于x非线性函数。

ps：这里的P(1−P)表示了某种事件的比值比（odds ratio）。

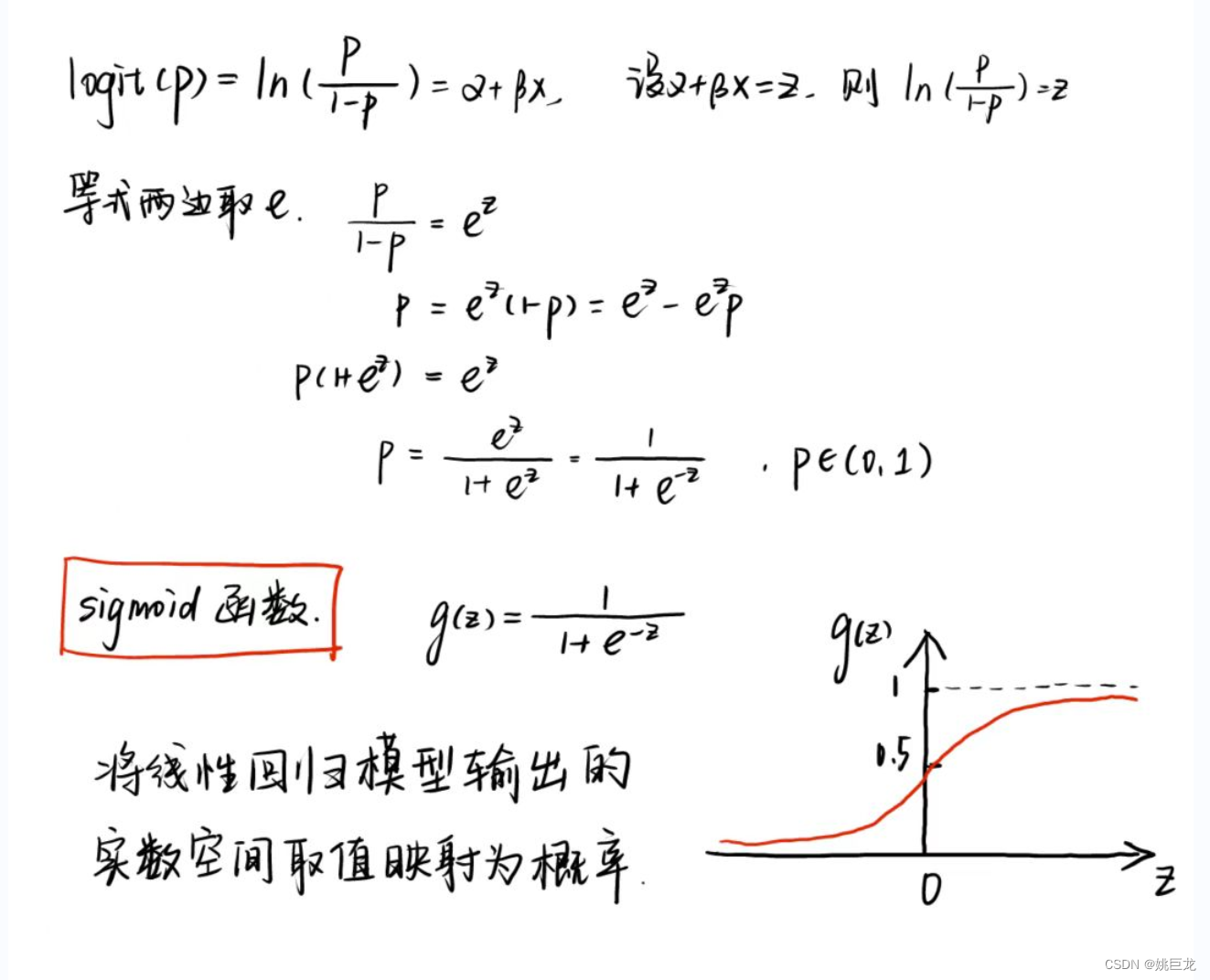
（二）模型的建立与检验

所谓估计参数，就是根据收集到的x变量和y变量的观察值，估计回归系数和回归系数估计值的标准误。

在Logistic回归分析模型中，回归系数的估计方法通常是最大似然法。为了简单起见，下面仅以一元Logistic回归模型为例，说明回归系数α和β的估计方法。

最大似然法就是选取使得总体真参数落在样本观察值领域里的概率达到最大的参数值作为真参数的估计值。因此，上述问题的最大似然函数如下：

在使用分析流行病学的方法研究疾病病因时，非条件Logistic模型是用于分析队列或病例——对照研究成组资料的统计方法，既可以进行因素筛选，也可以用于混杂因素的控制，后者应用的最为多见。

也就是说在病因学研究中，经常分析各危险因素与疾病发生的关系，要求资料要有均衡性。当影响结果的混杂因素较多，难以满足均衡可比性的要求时，就会给结果带来偏性。

为了正确说明疾病与危险因素的关系，就需要控制存在的混杂因素，Mantel-Haenszel分层分析的方法相当成功地解决了这一课题，但有其局限性，即随着控制因素的增加，分层越来越细时，每层的观察例数会越来越少，甚至会有零值出现，对相对危险度的估计带来了一定的困难或结果的不准确。

非条件Logistic回归模型能克服这些不足之处，可以对危险因素的定量测定值进行分析，已经逐渐被广泛应用。

（三）R程序

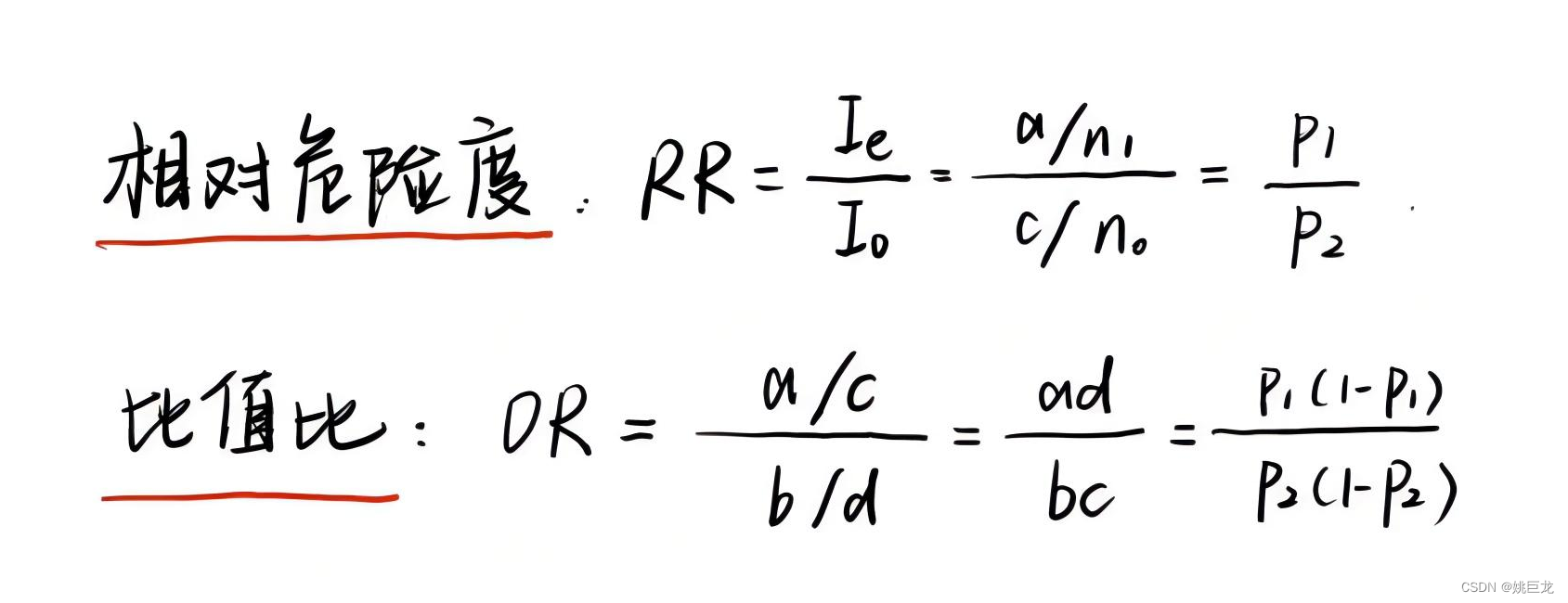
• 相对危险度表示暴露在危险因子下的发病率与不暴露在危险因子下的发病率的比。
• 比值比表示暴露在危险因子下的发病率与不发病率之比，与非暴露在危险因子下的发病率与不发病率之比的比。
• 当发病率很低时，OR≈RR。下面考虑Logistic回归模型系数的实际意义。

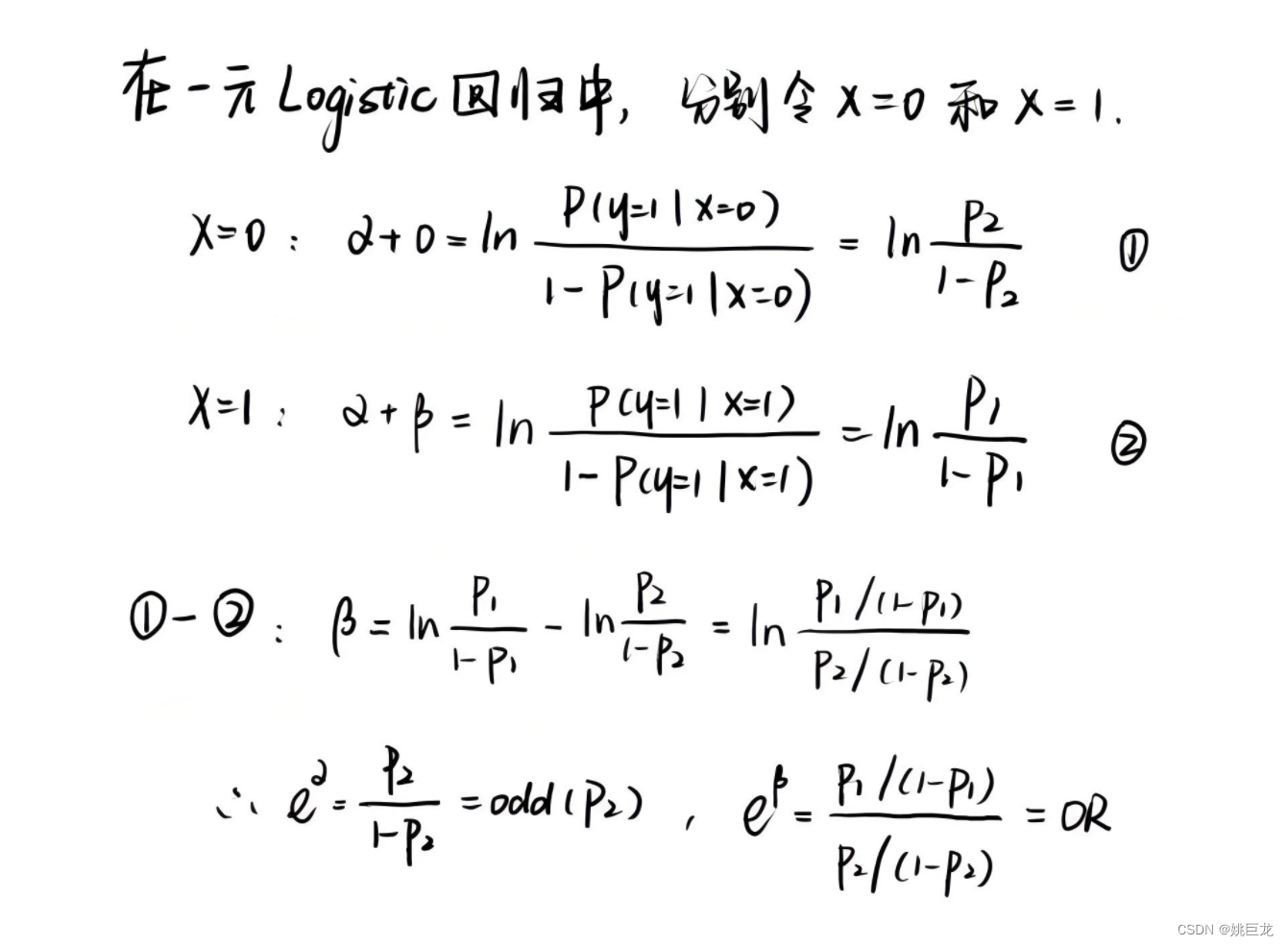
由于eβ=OR，而当发病率很低时，OR≈RR，因此这时eβ≈RR，也就是说，eβ近似地表示了相对危险度，即暴露下的发病率与非暴露下的发病率之比。eα=odds(P2)，而p2是非暴露下的发病率，所以eα等于非暴露下发病率与未发病率之比。

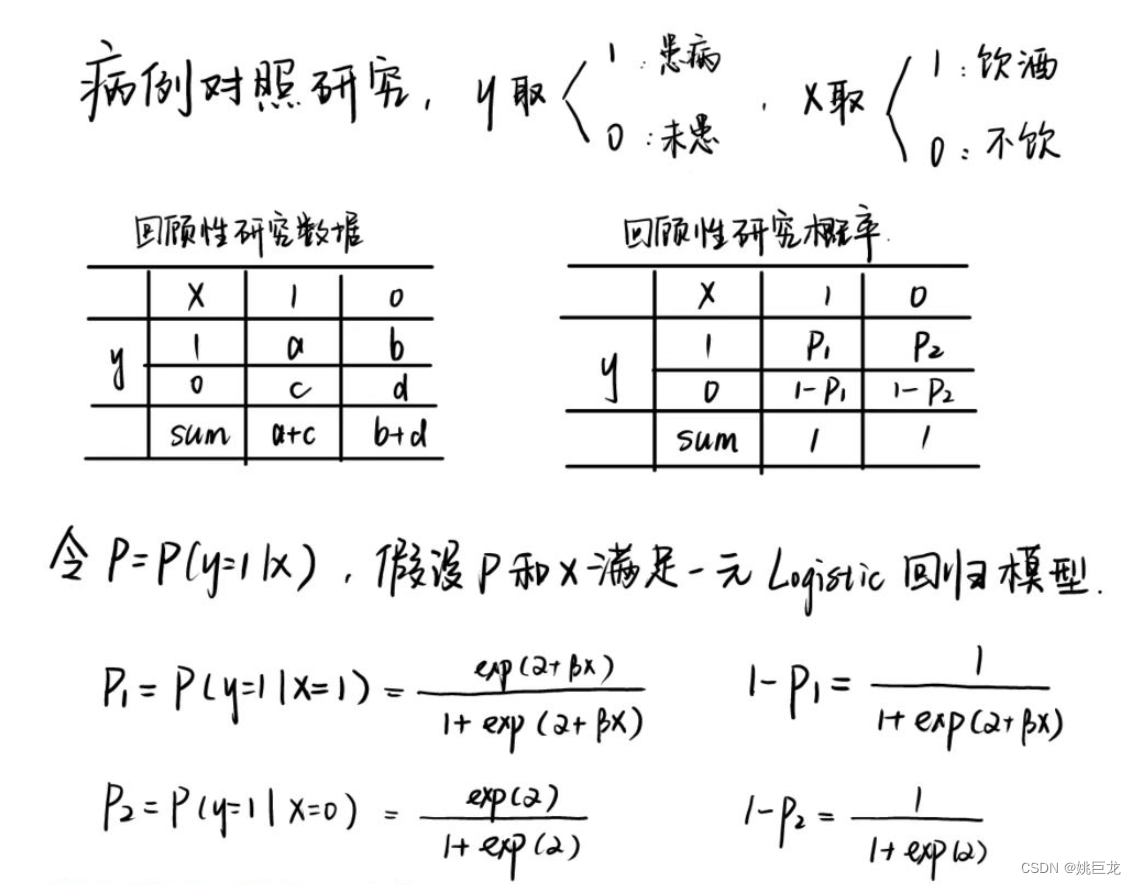
例1. 病例对照研究

研究吸烟、饮酒与食管癌关系的病例对照研究，并作Logistic回归分析：

设y=1表示患有食管癌，y=0表示未患食管癌。令x1=1表示吸烟，x1=0表示不吸烟；x2=1表示饮酒，x2=0表示不饮酒。下面采用Logistic回归模型进行分析。

R程序如下：

data <- read.table ("data.csv", header=TRUE, sep=",")
attach(data)
fit <- glm(y~ x1+ x2 ,  family= binomial(), data=data)
summary(fit)
coefficients(fit)
exp(coefficients(fit))
exp (confint(fit))
detach (data)

• 输出结果1
  
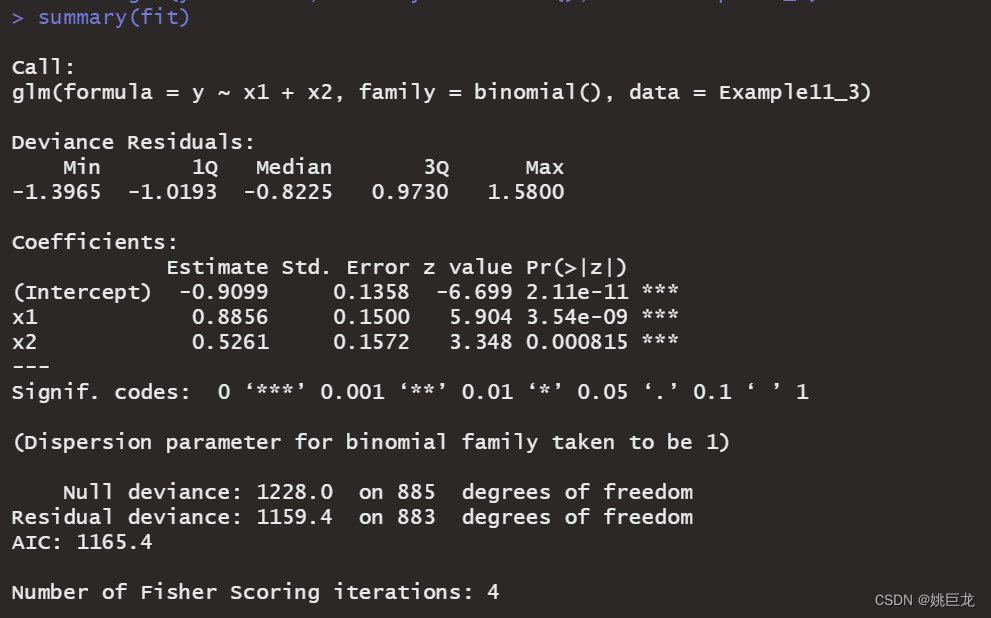
  因变量y取值的排列顺序是从大到小，所以系统输出的是y=1时的概率模型。上图输出结果表明自变量x1（P<0.0001）和x2（P=0.0008）的回归系数在统计意义上与0有显著性差异。

• 输出结果2
  
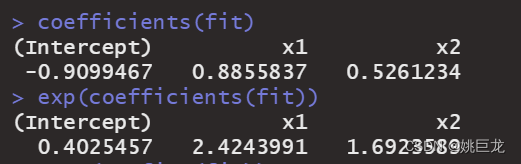
  上图为参数的OR值以及95%可信区间。因变量y对自变量x1和x2的Logistic回归模型如下：$$logit(p)=-0.9099+0.8856\ast x_1+0.5261\ast x_2$$

• 输出结果3
  
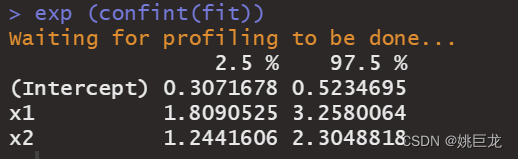
  上图为参数的95%可信区间，两个可信区间都不包括0，表明参数有显著性意义。

例2. 危险因素的交互影响

对于上例研究吸烟、饮酒与食管癌关系的病例对照研究资料，分析方法中没有考虑到吸烟与饮酒的交互作用，本例分析吸烟、饮酒危险因素对患食管癌的影响程度以及它们的交互影响程度。

• OR($x_1$ | 对任意固定的$x_2$)=2.424，表示消去了饮酒因素的影响后，吸烟者患食管癌的概率是不吸烟者患食管癌的2.424倍；
• OR($x_2$ | 对任意固定的$x_1$)=1.692，表示消去了吸烟因素的影响后，饮酒者患食管癌的概率是不饮酒者患食管癌的1.692倍。
• 设y=1表示患有食管癌，y=0表示未患食管癌。
• 令$x_1$=1表示吸烟，$x_1$=0表示不吸烟；$x_2$=1表示饮酒，$x_2$=0表示不饮酒。

因此，$x_1$和$x_2$的交叉水平有4个，建立4个哑变量分别代表这4个水平，记为 $x_{11}$、$x_{10}$、$x_{01}$、$x_{01}$，它们表示4种不同的生活方式，即$x_{11}$表示既吸烟又饮酒，$x_{10}$表示吸烟但不饮酒，$x_{01}$表示不吸烟但饮酒，$x_{00}$表示既不吸烟又不饮酒。

将前3个哑变量放进模型，则可得到前3种生活方式相对于最后一种生活方式患食管癌的相对危险度。

R程序如下：

data1 <- read.table ("data1.csv", header=TRUE, sep=",")
attach(data1)
data1$x11  <- ifelse (x1==1 & x2==1, 1, 0)
data1$x10  <- ifelse (x1==1 & x2==0, 1, 0)
data1$x01  <- ifelse (x1==0 & x2==1, 1, 0)
data1$x00  <- ifelse (x1==0 & x2==0, 1, 0)
fit <- glm(y~ x11 + x10 + x01 ,  family= binomial(), data=data1)
summary(fit)
coefficients(fit)
exp(coefficients(fit))
exp (confint(fit))
detach (data1)

• 输出结果1
  
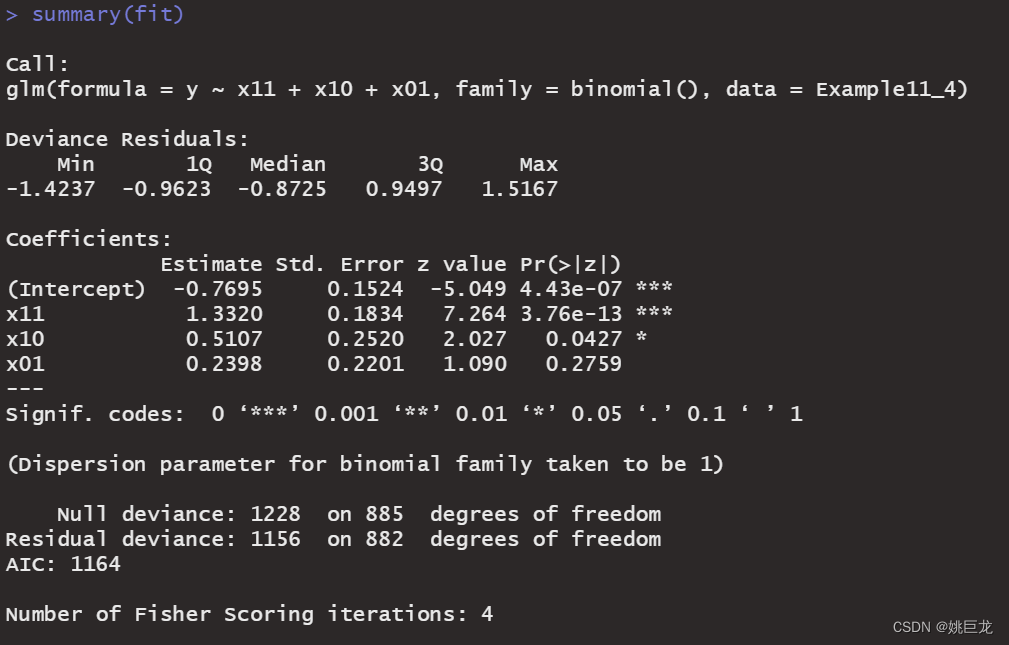
  因变量y取值的排列顺序是从大到小，所以系统输出的是y=1时的概率模型。结果表明自变量x11（P<0.0001）和x10（P=0.0428）的回归系数在统计意义上与0有显著性差异，但是x01的回归系数在统计意义上与0没有显著性差异。因变量y对自变量x11、x10和x01的Logistic回归模型如下：
  $$logit(p)=-0.7695+1.3320\ast x_{11}+0.5107\ast x_{10}+0.2398\ast x_{01}$$

• 输出结果2
  
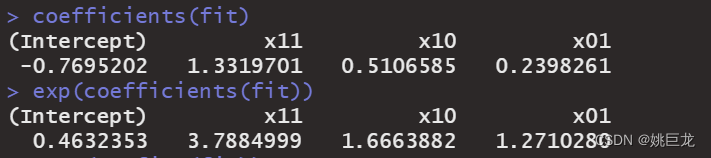
  上图为参数的OR值以及95%可信区间。因为4个哑变量中是以x00作为参照变量，因此OR（x11）=3.788表示既吸烟又饮酒者患食管癌的概率是不吸烟又不饮酒者的3.788倍，OR（x10）=1.666表示吸烟但不饮酒者患食管癌的概率是不吸烟又不饮酒者的1.666倍，OR（x01）=1.271表示不吸烟但饮酒者患食管癌的概率是不吸烟又不饮酒者的1.271倍。

• 输出结果3
  
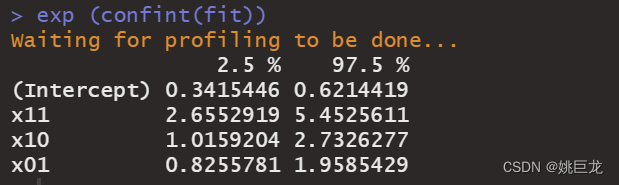
  上图为参数的95%可信区间。变量x11和x10的可信区间都不包括0，表明参数有显著性意义。变量x01的可信区间包括0，表明参数没有显著性意义。

四、条件logistic回归模型

（一）介绍

医学研究中的配对病例对照研究资料，可以使用条件Logistic回归模型来分析。

条件Logistic回归模型和非条件Logistic回归模型的区别在于：参数的估计是否用到了条件概率。

所谓的配对病例对照研究，指的是在病例对照研究中，对每一个病例配以性别、年龄或其他条件相似的一个（1∶1）或几个（1∶M）对照，然后分析比较病例组与对照组以往暴露于致病因素的经历。

分析配对病例对照研究资料所用的条件Logistic回归模型中参数的估计方法，也是采用最大似然估计法，参数和模型的检验方法和非条件Logistic回归模型一样。

（二）R程序

R语言中采用clogit()函数进行数据分析

例3. 病例对照研究

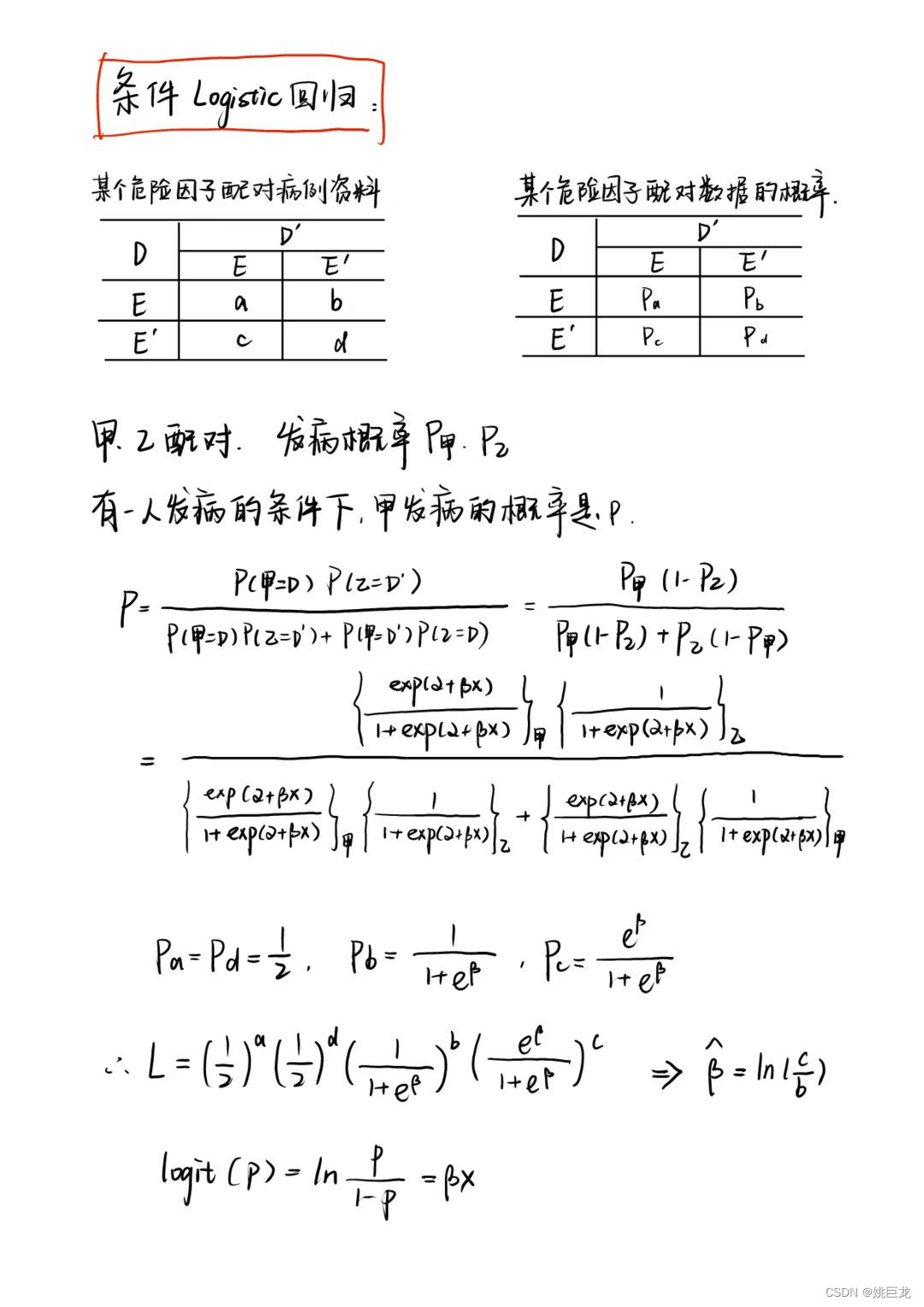
某研究机构为了研究胃癌与饮酒的相关关系，收集了病例对照资料如下表所示，其中D和D′分别表示患有胃癌和未患有胃癌，E和E′分别表示饮酒和不饮酒。用条件Logistic回归模型分析饮酒对胃癌的影响：

R程序如下：

install.packages("survival")
library(survival)
data2 <- read.table ("data2.csv", header=TRUE, sep=",")
attach(data2)
model <- clogit(outcome~ exposure+ strata(id))
summary(model)
detach(data2)

输出结果：

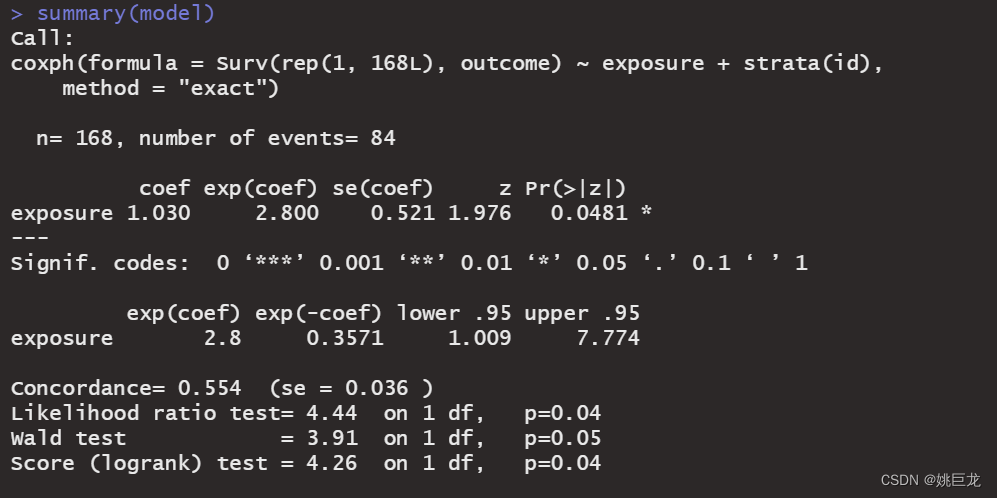
• 从输出结果图中可以看出截尾事件和终点事件，本例没有截尾事件。
• 模型的检验结果：模型较好地拟合了研究数据，有统计学意义（P=0.0481）
• 描述统计量：HR=2.8，可以认为饮酒研究对象患有胃癌的概率是不饮酒研究对象的2.8倍。