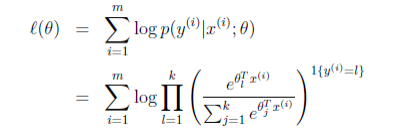上一篇博客中我们说到线性回归和逻辑回归之间隐隐约约好像有什么关系，到底是什么关系呢？我们就来探讨一下吧。（这一篇数学推导占了大多数，可能看起来会略有枯燥，但这本身就是一个把之前算法统一起来的抽象模型，从一个更高的角度给出了一个更具泛化能力的方法，还是很有意义的。）

1. 指数分布族

　　首先，我们先来定义指数分布族（exponential family），如果一类分布可以写成如下的形式，那么它就是属于指数分布族的：

$$p(y;\eta)=b(y)exp(\eta^TT(y)-a(\eta))$$
这里 $\eta$叫做分布的 自然参数（natural parameter），或者叫 标准参数（canonical parameter）；T(y)是 充分统计量（ sufficient statistic），对于我们考虑的大多数分布， $T(y)=y$；然后 $a(\eta)$叫做 log partition function（不会翻译，就强不翻了。。。）。 $e^{- a(\eta)}$实际上是一个标准化的常数，用来保证这个分布的和为1。
　　这个指数分布族是何方神圣呢？为什么要先讲它呢？因为我们前面讲过的伯努利分布和高斯分布都可以归为指数分布族的一种。什么？这两个长得毫不相关的分布可以归为一起吗？我的天呐，这么神奇吗？（小岳岳脸）哈哈，是的！下面我们就来说一说这是怎么回事。
　　伯努利分布就是我们前面讲的y只能取0和1时的情况，它就可以变成指数分布族的形式，我们试一试：

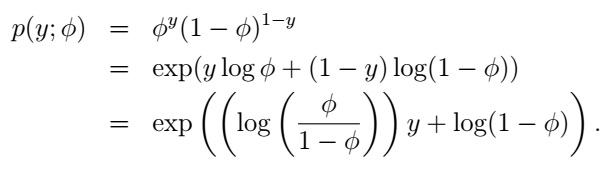
　　这里，我们选择自然参数 $\eta=log(\phi/(1-\phi))$，诶，有个很有趣的事情：如果我们用 $\eta$表示 $\phi$，我们可以得到 $\phi=1/(1+e^{-\eta})$，是不是很眼熟？这不就是sigmoid function吗？没错！更神奇的还在后面呢。现在我们把伯努利分布写成了指数分布族的形式。什么？不是很明显？它们的对应关系是这样的：
　　
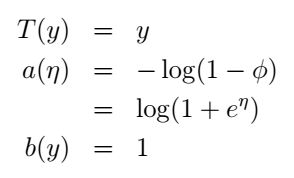
　　好，我们再来说高斯分布。前面我们说了，高斯分布的 $\sigma^2$对模型的结果是没有影响的那我们就干脆令它为1好了（其实如果我们把它当做变量，依然行的通，只是得到的 $\eta$将会是二维的）。高斯分布也写成指数分布族的形式，推导是这样的：
　　
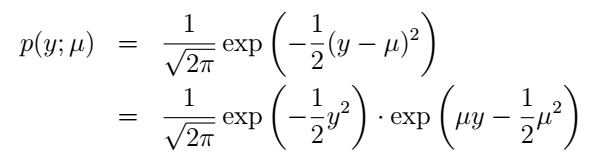
　　它与指数分布族的对应关系为：
　　
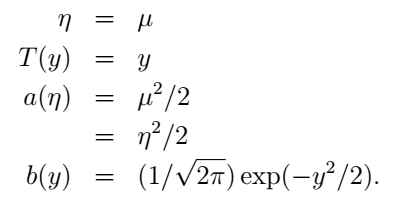
　　上面我们展示了伯努利和高斯分布，实际上，还有multinomial（后面将会谈到），泊松分布，gamma和指数分布，beta和狄里克雷分布等等都是属于指数分布族的。怎么样，这个广义线性模型还是有两下子的的，原来我们前面讨论的分类都可以统一为指数分布族的形式。但这还不够，我们怎么从指数分布族中推出我们想要的东西呢？下面我们就来看一看怎样通过构造广义线性模型来解决实际问题。

2. 构造GLMs

　　现在我们来把之前的分类问题扩展一下。生活中的很多事物肯定不止一个种类，我们来考虑多类别的分类问题，讨论一下如何利用GLMs来解决。
　　首先，和之前一样，我们构造模型都是有一定的条件的。我们先来作三个假设：
　　1. $y|x;\theta\sim ExpoentialFamily(\eta)$。这当然是必须的，我们就是要用指数分布族来解决问题嘛。
　　2. 我们的目标是给定x，预测T(y)期望。比如我们刚才说了，大多数情况下T(y)=y，而在逻辑回归问题中，我们要预测的$h_\theta=p(y=1|x;\theta)=0\cdot p(y=0|x;\theta)+ 1\cdotp(y=1|x;\theta)=E[y|x;\theta]$。
　　3. 自然参数$\eta$满足$\eta=\theta^Tx$。
　　如果我们的问题需要满足这三个假设，那么我们就可以通过构造广义线性模型来解决。线性回归和逻辑回归都是满足这三个假设的，就可以使用这个模型。

2.1 普通的最小平方（Ordinary Least Squares）问题

　　在线性回归的最小平方问题中，目标变量y（在GLM的术语中也称作响应变量（response variable））是连续的，给定x，y的条件分布符合我们刚刚讨论过的高斯分布，均值为$\mu$。套用前面GLM的推导，我们有$\mu=\eta$。所以，我们可以得到线性回归的假设函数就是：

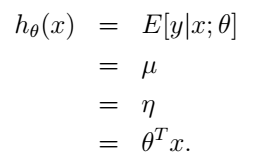
这样，我们就从广义线性模型的角度得到了线性回归的解决方案。

2.2 逻辑回归

　　在二元分类问题中，给定x，y服从我们刚才讨论的伯努利分布，均值为$\phi$。同样利用前面的推导我们可以得到逻辑回归的假设函数就是：

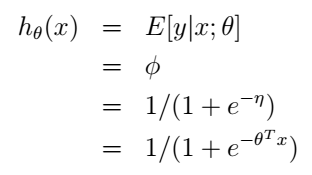
最后一个等号是由前面第3个假设的到的。同样的，我们也从广义线性模型的角度得到了逻辑回归的解决方案。这里，我们就知道了为什么在逻辑回归中我们的假设函数要用sigmoid function了吧，并不是凭空才出来的喔。
　　这里我们介绍几个术语。$g(\eta)=E[T(y);\eta]$被称为canonical response function，它的反函数$g^{-1}$，被称为canonical link function。

2.3 Softmax Regression

　　好了，铺垫了这么久，我们终于可以考虑我们的多类别分类的问题了，我们首先用multinomial distribution来给它建立模型。假设我们的类别$y\in\{1,2,\dots,k\}$。我们可以用一个k维的向量来表示分类结果，当y=i时，向量的第i个元素为1，其它均为零。但这样做是存在冗余的，因为如果我们知道了前k-1个元素，那么第k个其实就已经确定了，也就是说，这k个元素不独立。因此我们可以只用k-1维向量来表示，每一维对应的参数为$\phi_i$。为了方便，我们也使用$\phi_k$，但应该记住，它并不是一个真正的参数，它只表示$\phi_k=1-\sum_{i=1}^{k-1} \phi_i$。这样我们可以定义：

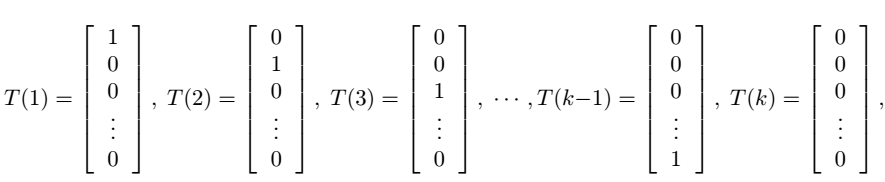
注意，这里就和前面T(y)=y不一样了，这里的T(y)是一个向量了。我们用$(T(y))_i$表示T(y)的第i个元素。
　　为了表示方便，我们用符号$1\{{\cdot}\}$表示判断，{}中的表达式为真时输出1，为假时输出0。于是我们有$(T(y))_i=1\{y=i\}$，它表示只有当y=i时$(T(y))_i$才不为零。另外，由于$\phi_i$表示第i个类别的概率，我们有$E[(T(y))_i]=P(y=i)= \phi_i$。
　　好，我们仿照前面二元分类的过程，来说明这个multinomial也是属于指数分布族的：
　　
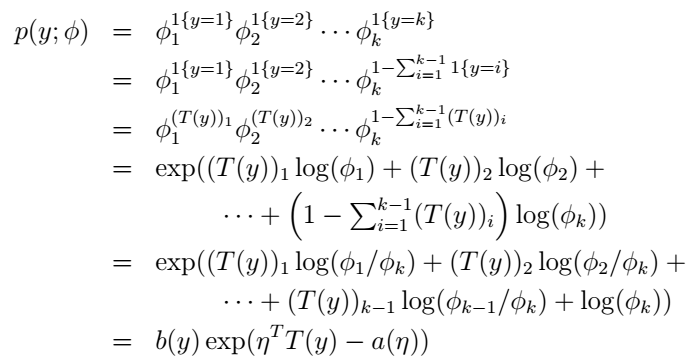
　　这里，
　　
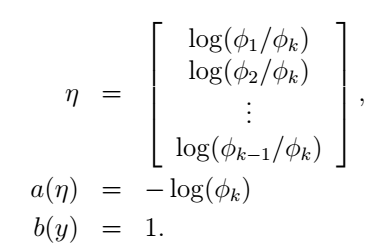
　　我们可以看到：
　　
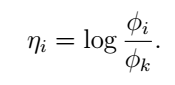
　　当i=0时上式为零。我们的目的是为了得到参数$\phi$，于是
　　
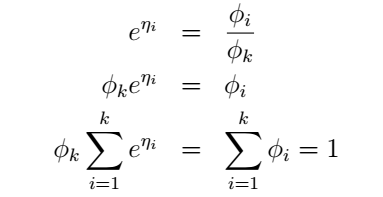
　　最后我们终于得到：
　　
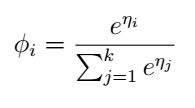
　　我们再利用假设3，就可以得到参数$\phi$了：
　　
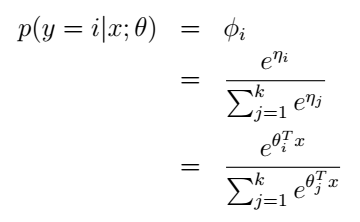
　　这个模型就被称为softmax regression，它是逻辑回归在多类别情况下的扩展。综合起来，我们的假设函数的输出为：
　　
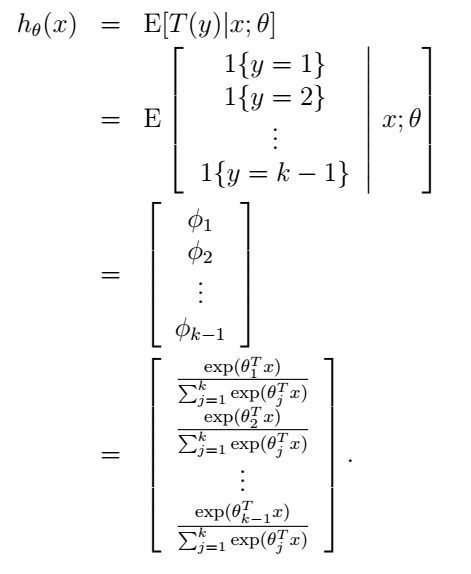
　　最后就是参数的学习了。我们依然可以使用最大似然的方法来学习$\theta$，似然函数为：
　　
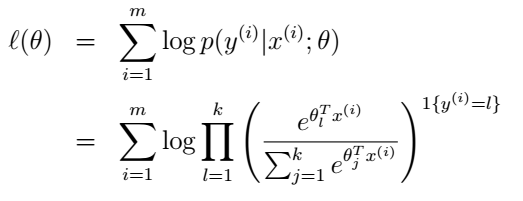
　　然后使用梯度上升或牛顿方法等来求出使似然函数最大的$\theta$值，就大功告成了！