汉诺塔递归算法（Python编程）

article/2025/9/9 8:03:28

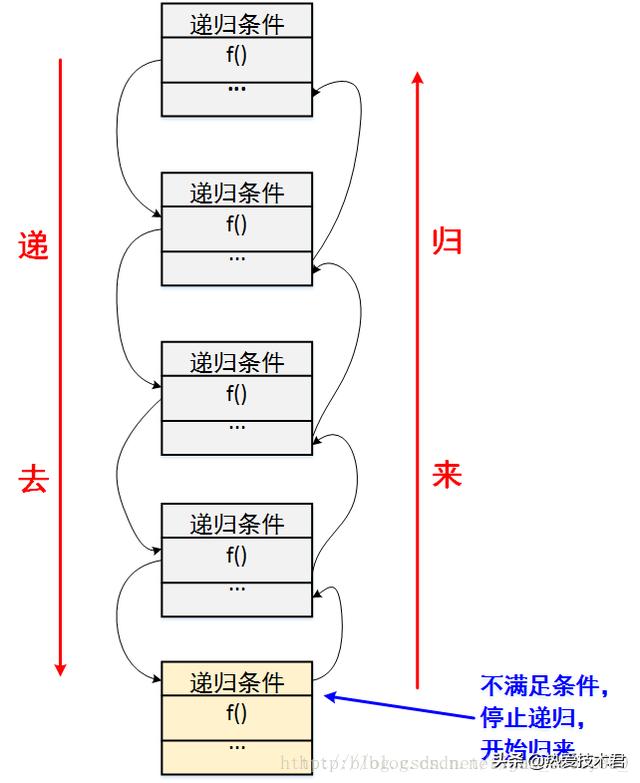
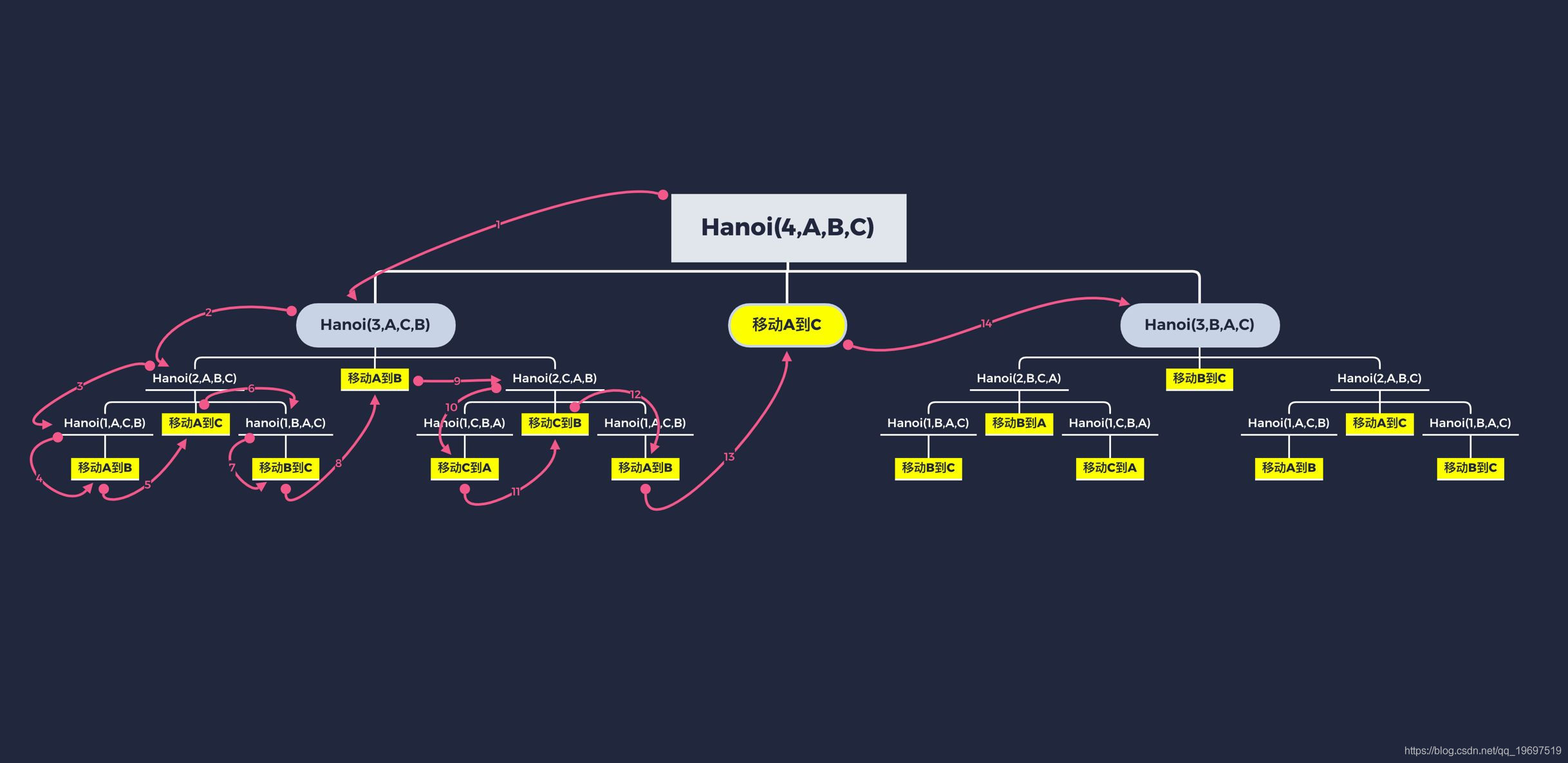
一、问题描述。
汉诺塔是学习计算机递归算法的经典入门案例，是一个数学难题。其问题为如何将所有圆盘从A移动到C，要求一次只能移动一个盘子，盘子只能在3个标杆（A/B/C）之间移动，更大的盘子不能放在更小的盘子上面。请用Python编写一个汉诺塔的移动函数，采用递归方法解决这个问题，要求输入汉诺塔的层数，输出整个移动流程。

二、问题分析。
在这里插入图片描述
如图，假设A上有5层的圆盘。
首先，我们将A上的圆盘分为底层1个与上层4个，将上层4个圆盘视为一个整体移动到B上，B作为中转站。然后把A上最大的圆盘移动到C上。

其次，我们来看B上剩下的4个圆盘，按照以上方法（可以把4个盘子重新放回A上），将其分为底部1个盘子与上方3个盘子，把3个盘子视为整体放到B上，再将A上的1个盘子移动到C上。
在这里插入图片描述

以此类推，我们可以找到实际操作中我们要移动的第一个盘子（最小的那个盘子）。
最后一张图可以把C上圆盘当做不存在，视为只有2个圆盘时的移动过程。

三、编写程序。
1、代码示例：

def move(n,A,B,C):if n == 1 :print (A,"->",C)else :move(n-1,A,C,B)move(1,A,B,C)move(n-1,B,A,C)
n=eval(input("请输入递归层数:"))
move(n,'A','B','C')

2、运行结果：
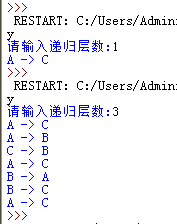
在这里插入图片描述

四、总结。
这个问题对我来说难度系数比较高，理解了挺久的。
操作时不是真的将4个圆盘一起移动到B上，因为一次只能移动一个圆盘。将4个圆盘看做一个整体来移动是因为我们要利用计算机来解决这个递归问题。
我们可以把几个盘子视为整体移动后得到的结果想象为经过多个步骤才得到的，而我们现在要寻找的就是这些复杂步骤的起始步骤。
这也就是利用计算机递归算法层层深入找到的，每次重复的操作可以将C上的盘子视为不存在，这样可以更好地理解递归思想。