汉诺塔介绍
汉诺塔简单介绍:
有三根相邻的柱子,假定从左到右为A,B,C,A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘,要把所有盘子一个一个移动到柱子B上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。
递归的移动思路
将圆盘的移动分解看作三步:
第一步:
将最下面最大圆盘的上面所有圆盘视作n-1个圆盘,需要从借助C柱移动到B柱上
第二步:
将最大的圆盘移动到C柱上
第三步:
将n-1个圆盘借助A柱移动到C柱上
代码实现
count = 0
def hanoi(n, a, b, c):
global count
if n > 0:
hanoi(n - 1, a, c, b)
print(f'移动 {a} 到 {c}')
count += 1
hanoi(n - 1, b, a, c)
hanoi(4, 'A', 'B', 'C')
print(f"一共移动{count}步")
假设只有4个圆盘
运行的结果为:
移动 A 到 B
移动 A 到 C
移动 B 到 C
移动 A 到 B
移动 C 到 A
移动 C 到 B
移动 A 到 B
移动 A 到 C
移动 B 到 C
移动 B 到 A
移动 C 到 A
移动 B 到 C
移动 A 到 B
移动 A 到 C
移动 B 到 C
一共移动15步
汉诺塔递归图解:
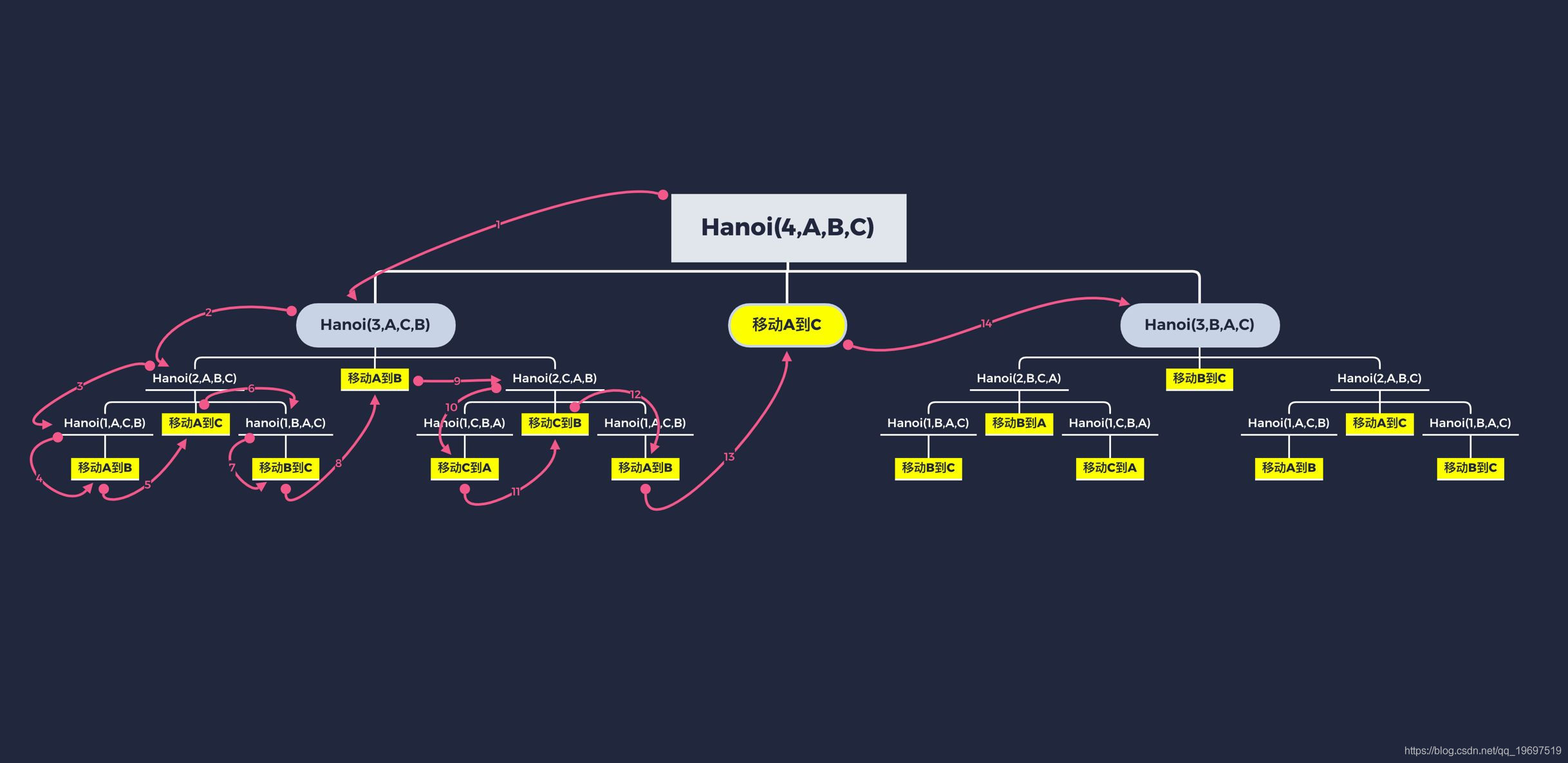
首先调用函数Hanoi(4,A,B,C)判断N>0之后,继续调用Hanoi(3,A,C,B),然后继续判断N>0再进入Hanoi(2,A,B,C),之后再进入Hanoi(1,A,C,B),因为判断完大于0之后,再调用Hanoi的时候,变成Hanoi(0,A,B,C),此时N为0,不会再进行递归了,就会跳出到Hanoi(1,A,C,B)下执行print打印[从A移动到B],执行完之后就会再跳出到Hanoi(2,A,B,C)函数的print打印 [从A移动到C] ,之后执行Hanoi(1,B,A,C),然后打印从B移动到C。此时Hanoi(2,A,B,C)执行完毕跳到Hanoi(3,A,C,B)这一层继续向下执行print打印从A移动到B。
以此类推一直到最后,程序中打印的内容用在结构图中用黄色高亮标出来了。然后标注了从Hanoi(4,A,B,C)一直到Hanoi(3,A,C,B)执行的顺序。
可以通过画图深入理解递归,和汉诺塔的递归结构。