一、什么是递归

方法调用自己的行为就是递归，递归必须要有终止条件，不然它会无限递归。

1.先来看一下一个递归的例子

此程序的Fact方法从大到小地一级一级地调用自己，直到参数为1，然后就开始返回一级一级的从小到大地累乘，然后就计算出number的阶乘了。

static int Fact(int num)
{if (num <= 1){return num;}else{return num * Fact(num - 1);//调用自己，这一步是关键}
}

2.递归的基本原理

以下是《C#图解教程》对于递归的描述：

1. 除了调用其他方法，方法也可以调用自身，这叫做递归。
2. 调用方法自身的机制和调用其他方法其实是完全一样的，都是为每一次方法调用把新的栈帧压入栈顶。
   

我个人认为递归就是把你要干的事情抽象一个成可以有限步数解决的方法，然后某一步解决不了就再调用这个方法，直到可以解决（结束递归的条件）这个问题就返回。
下面再看一个具体的例子来了解递归。

二、汉诺塔问题

1.汉诺塔的故事

汉诺塔由法国数学家爱德华·卢卡斯创造，他曾经编写了一个印度的古老传说：

在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

2.回到编程，汉诺塔问题主要就是解决这个问题：

有A、B、C三根针，A上从小到大放着n层盘子，要从A上所有的盘子移动到C盘上。
条件是一次只能移动一个盘子，无论什么时候小盘子必须在大盘子上面。
汉诺塔问题求的是把盘子从A移到C总共的移动次数是多少。

这是我之前追踪4层汉诺塔运行步骤画的笔记

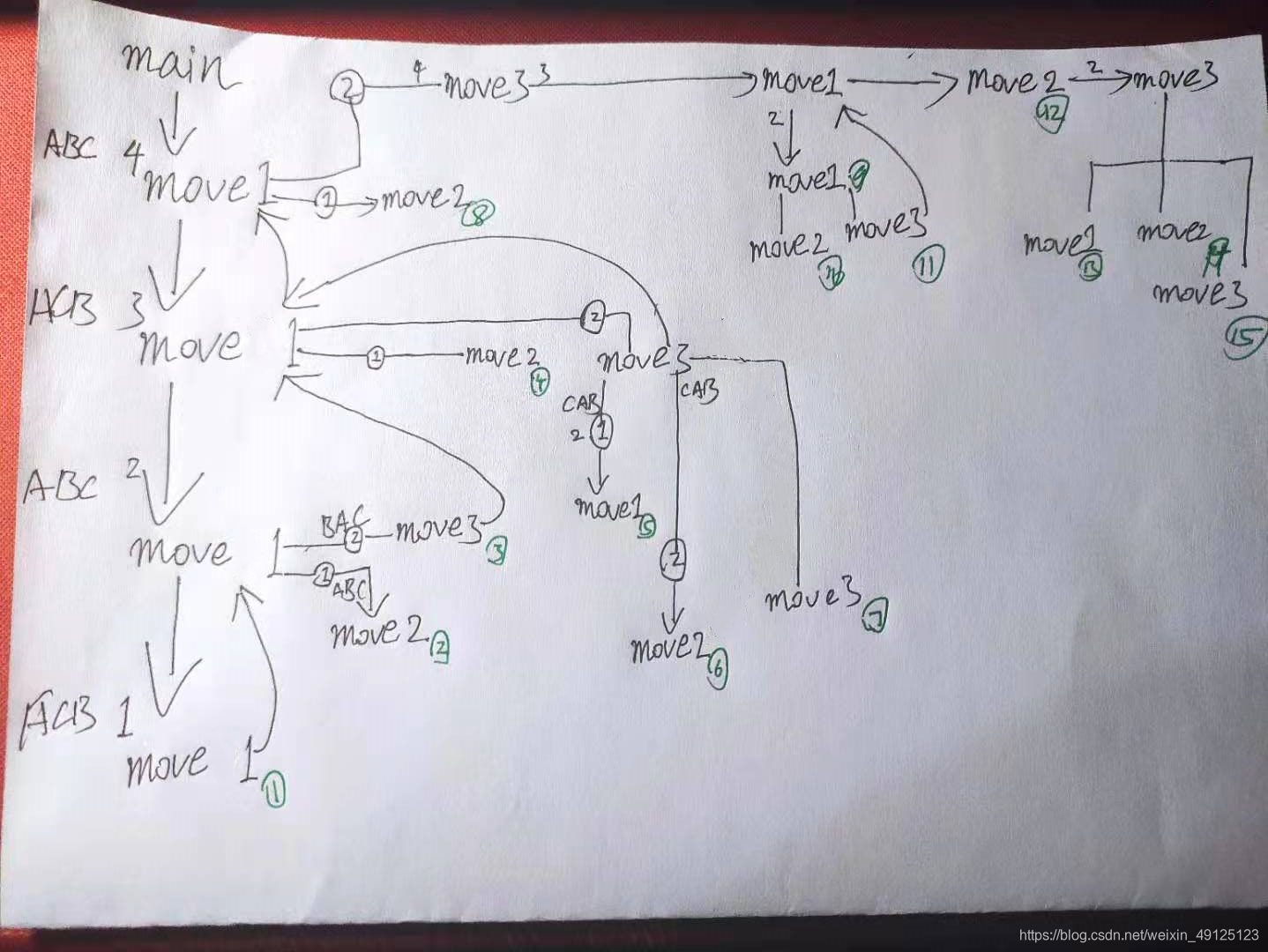
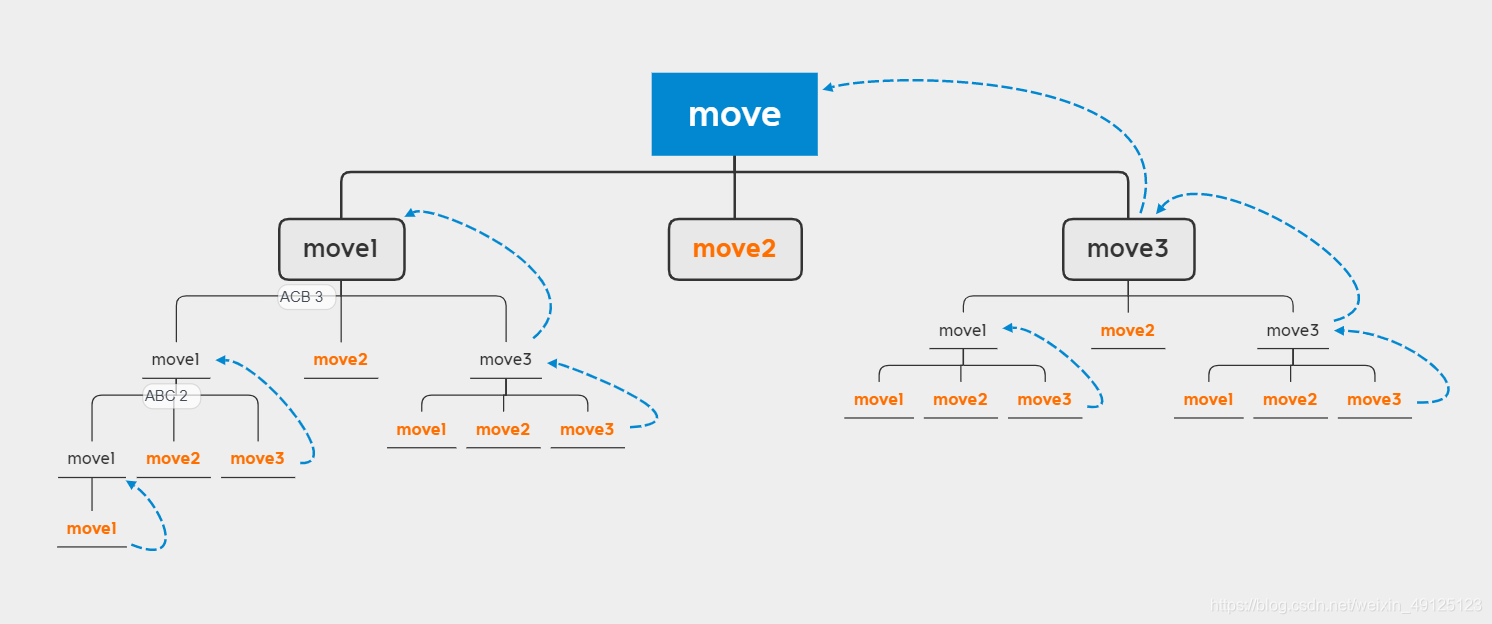
事实证明，没多大帮助。
要想理解递归必须要放弃理解递归，放弃跟踪全程步骤。
解决问题是计算机的事，你只要明确要把每一步怎么传给计算机，递归两层之间怎么交接，以及递归结束的条件就可以。

3.怎么解决汉诺塔问题

要解决汉诺塔问题就要用到递归思想，这里拿四层汉诺塔举例子：

要完成四层汉诺塔，需要先把第四层盘子从A柱放到C柱，而要把第四层盘子放到C柱，就要把上面三层的盘子放到B柱：

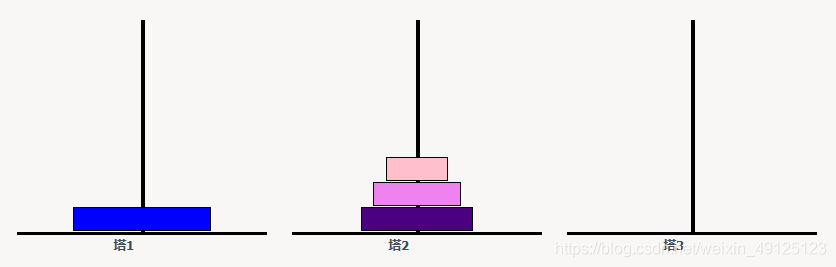
那么要把这三层盘子移到B柱，那么就要先把第三层盘子移到B柱。
要把第三层盘子移到B柱，就要把第二层盘子移到C柱子。
要把第二层盘子移到C柱，就要把第一层盘子移到B柱子。
移动一层汉诺塔到另一个柱不简单吗？
这样子把问题解决了，第四层盘子就可以移动到C柱上了。
然后把剩下的三层汉诺塔也按照上面的思想，就可以移动到C柱上了。

4.具体代码实现

把大象装进冰箱需要多少步

1. 把冰箱门打开
2. 把大象放进去
3. 把冰箱门关上

把汉诺塔放到C柱需要多少步

1. 把底层上面的盘子放到B柱
2. 把最底层盘子放到C柱
3. 把B柱那些盘子放到C柱

抽象一下就是：

1. 把n-1层盘子从起点移到暂存区
2. 然后把第n层盘子从起点移到终点
3. 然后把n-1层盘子从暂存区移到终点

在这里可以创建一个Move方法来移动盘子

static void Move(int pile, char src, char tmp, char dst)
{}

src就是源起点，tmp就是暂存区，dst就是终点

最外层的Move方法完成的是把pile层汉诺塔从src经过tmp移动到dst

现在要把大象装进冰箱了

在Move方法里面调用Move方法来解决之后的问题：

1. 把冰箱门打开

Move(pile - 1, src, dst, tmp);

这层Move完成的是把pile-1层汉诺塔从src经过dst移动到tmp

---

2.把大象塞进去

Move(1, src, tmp, dst);

这层Move完成的是把最底层汉诺塔盘子从src直接移动到dst

---

3.把门关上

Move(pile - 1, tmp, src, dst);

这层Move完成的是把pile-1层汉诺塔从tmp经过src移动到dst

Move方法完整代码：

static void Move(int pile, char src, char tmp, char dst){if (pile == 1)//pile=1问题就好解决了{Console.WriteLine($"{src} --> {dst}");steps++;return;}Move(pile - 1, src, dst, tmp);Move(1, src, tmp, dst);Move(pile - 1, tmp, src, dst);}

每一层Move方法都有他自己的起点、暂存区和终点，我们只需要把上一层的起点、暂存区和终点传过去就行了。

5. 完整代码

以下是完整代码：

using System;namespace Hanoi
{class Program{public const int MAX_VALUE = 30;//声明最大值常量public static int steps = 0;static void Main(string[] args){int levels = 0;Console.Write($"输入汉诺塔层数（1~{MAX_VALUE}）: ");levels = int.Parse(Console.ReadLine());if (levels > 0 && levels < MAX_VALUE){Move(levels, 'A', 'B', 'C');Console.WriteLine($"一共移动了{Program.steps}次。");Console.ReadKey();return;}Console.WriteLine("输入范围错误");Console.ReadKey();}static void Move(int pile, char src, char tmp, char dst){if (pile == 1)//pile=1问题就好解决了{Console.WriteLine($"{src} --> {dst}");steps++;return;}Move(pile - 1, src, dst, tmp);Move(1, src, tmp, dst);Move(pile - 1, tmp, src, dst);}}
}

运行结果如下：