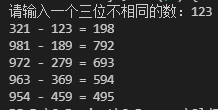
任意一个5位数，比如：34256，把它的各位数字打乱，重新排列，可以得到一个最大的数：65432，一个最小的数23456。求这两个数字的差，得：41976，把这个数字再次重复上述过程（如果不足5位，则前边补0）。如此往复，数字会落入某个循环圈（称为数字黑洞）。
比如，刚才的数字会落入：[82962, 75933, 63954, 61974] 这个循环圈。


请编写程序，找到5位数所有可能的循环圈，并输出，每个循环圈占1行。其中5位数全都相同则循环圈为 [0]，这个可以不考虑。


循环圈的输出格式仿照：
[82962, 75933, 63954, 61974]


其中数字的先后顺序可以不考虑。

本以为会是比较容易能做出来的，但是由于没有考虑所有的情况，加上过年这几天吃昏头了，做了3个多小时，好在总算是出来了。

对于黑洞数的定义，题目很清晰，要获得数列中的下一个数，就必须对给定的数的每一位重新排序求得最大和最小，而且还有可能出现位数不足五位的情况，所以，在拆数的时候，我固定就拆5次，这样，不足的位数就可以被0补上，从而满足题目的要求。，查找循环圈也比较容易，麻烦就麻烦在重复的循环圈如何判别，这里我是用这样的方法：对于每一个数，都有一个判别标志位visited[]，每一次读入一个数，就把这个标志置1，这样，当我们得到一个含有循环圈的数列之后，每一个数在大循环中都不可能出现，但还存在一种情况，就是通过一个从未被访问的数，却进入之前进入过的一个循环圈，解决的方法是：在读数的时候把每含有循环圈的数列的每一个数的标志位再加1，也就是2，这样既不会影响上面循环中重复位的判断，也可以避免通过不同的数进入同一个循环圈，因为当检测到某一个数的标志位为2时，不仅停止循环，而且通过flag标志阻止下面进行输出，这样就可以顺利求出所有的循环圈，也就是黑洞数。

#include<iostream>
#include<cmath>
#include<algorithm>
#include<memory.h>
#define N 90000
using namespace std;
int num[N];
int visited[100000];
int s[N];
bool cmp(int a,int b)
{return a>b;
}void init()
{int i;int n=10000;for(i=0;i<N;i++)num[i]=n++;memset(visited,0,sizeof(visited));
}int find(int t,int j)
{for(int i=0;i<j;i++)if(s[i]==t)return 0;return 1;
}int getMax(int n)
{int i;int T=0;int temp[5];for(i=4;i>=0;i--){temp[i]=n%10;n=n/10;}sort(temp,temp+5);for(i=0;i<5;i++){T=T+temp[i]*pow(10,i);}return T;
}
int getMin(int n)
{int i;int T=0;int temp[5];for(i=4;i>=0;i--){temp[i]=n%10;n=n/10;}sort(temp,temp+5,cmp);for(i=0;i<5;i++){T=T+temp[i]*pow(10,i);}return T;
}int main()
{int t,i,j,k,flag;init();for(i=10000;i<=99999;i++){if(visited[i])continue;//cout<<"i="<<i<<":"<<endl;memset(s,-1,sizeof(s));s[0]=i;j=1;flag=0;visited[i]=1;t=getMax(i)-getMin(i);while(1){if(t==0)break;//cout<<t<<endl;//getchar();//cout<<getMax(*it)<<' '<<getMin(*it)<<endl;//cout<<t<<endl;//cout<<find(t,j)<<endl;if(visited[t]>1){flag=1;break;}if(find(t,j)==1){s[j]=t;j++;visited[t]=1;}else break;t=getMax(t)-getMin(t);}if(flag==0&&t!=0){for(k=0;k<j;k++){visited[s[k]]++;if(s[k]==t)break;} for(;k<j;k++){visited[s[k]]++;cout<<s[k]<<' ';//getchar();}cout<<endl;}}return 0;
}