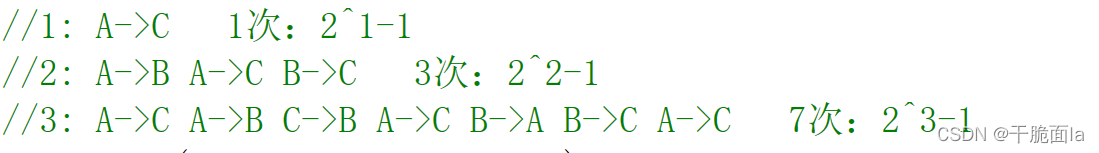递归算法 —— Hanoi汉诺塔游戏

article/2025/9/9 15:07:16

前言

博客主页：干脆面la的主页

gitte链接：干脆面la的gitee仓库

刚学习完递归函数接触汉诺塔问题的时候，汉诺塔问题困扰了我很久。博主花了很长时间理解这道题目，因此整理出了用递归解决汉诺塔问题的思路，希望对大家有所帮助。

如果认为博主的文章对你有所帮助
欢迎三连加关注
你们的支持是我最大的动力！

前言

1 汉诺塔的由来

2 图解1~3个圆盘的汉诺塔

2.1 1个圆盘的移动

2.2 2个圆盘的移动

2.3 3个圆盘的移动

3 核心思路

4 代码实现

4.1 模拟移动的过程

4.2 Hanoi的递归代码

4.3 完整代码

4.4 运行结果

5 总结

正文开始...

1 汉诺塔的由来

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

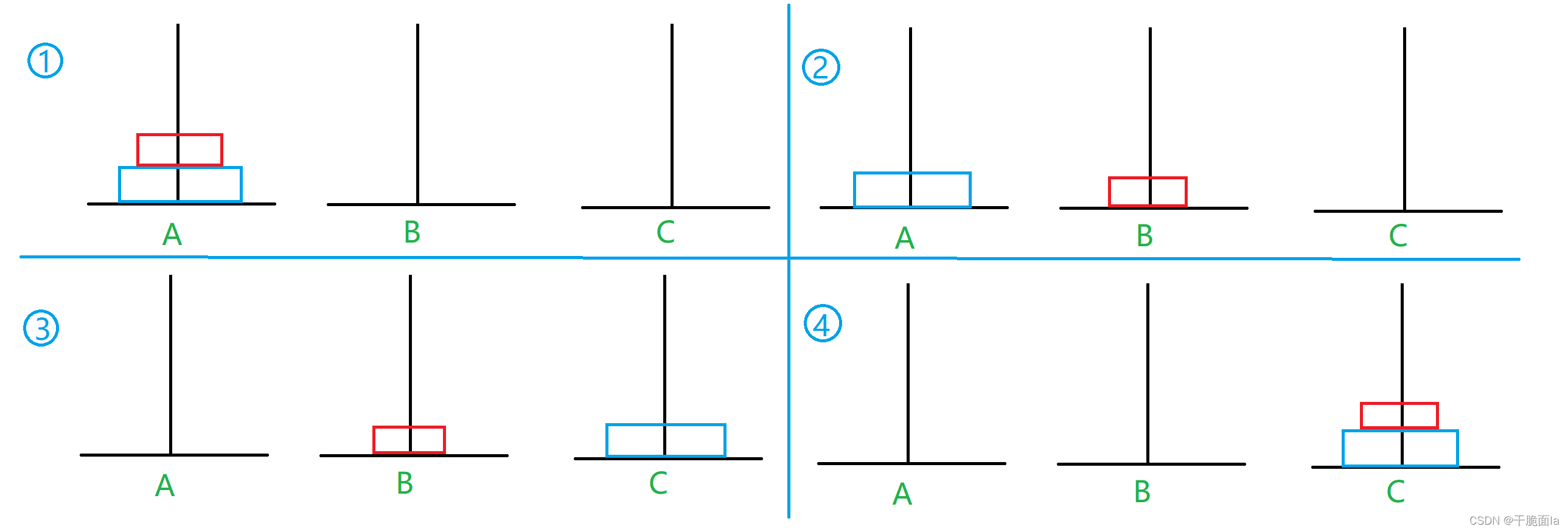
2 图解1~3个圆盘的汉诺塔

2.1 1个圆盘的移动

移动1次：A->C

2.2 2个圆盘的移动

移动3次：A->B A->C B->C

2.3 3个圆盘的移动

移动7次：A->C A->B C->B A->C B->A B->C A->C

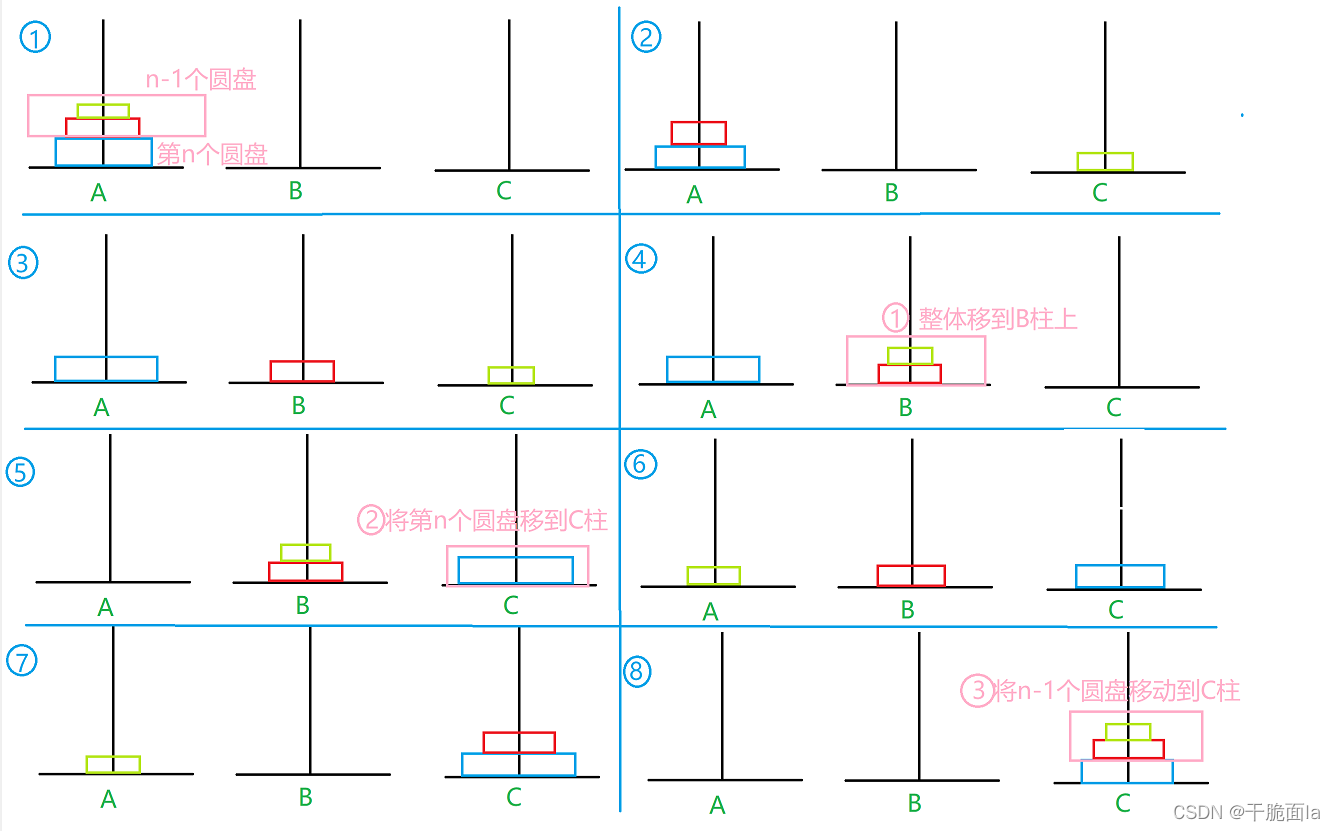
3 核心思路

对于三个圆盘以上的汉诺塔游戏便开始愈加困难，但是通过递归的思想我们可以将一个极其复杂的步骤简化为一个简单的步骤。

对比这三幅图，我们发现从2个圆盘开始，它们都必须经历的操作就是：(1)使n-1个圆盘整体移动到B柱（中转位置）上，(2)再使第n个圆盘移动到C柱（目的位置）上，(3)再将n-1个圆盘整体移动到C柱（目的位置）上。

上一操作中的第(1)步又可以细分到：将n-2个圆盘通过 (1)使n-2个圆盘整体移动到C柱（中转位置）上，(2)再使第n-1个圆盘移动到B柱（目的位置）上，(3)再将n-2个圆盘整体移动到B柱（目的位置）上。

上一操作中的第(3)步又可以细分到：将n-2个圆盘通过 (1)使n-2个圆盘整体移动到A柱（中转位置）上，(2)再使第n-1个圆盘移动到C柱（目的位置）上，(3)再将n-2个圆盘整体移动到C柱（目的位置）上。

以此类推......

综上所述：本题应该使用递归的方法，让题目化繁从简，使一个极其复杂的步骤简化为简单的步骤。

4 代码实现

4.1 模拟移动的过程

void move(char pos1, char pos2)
{printf(" %c->%c ", pos1, pos2);
}

4.2 Hanoi的递归代码

n:盘子个数 pos1:起始位置 pos2:中转位置 pos3:最终位置

void Hanoi(int n, char pos1, char pos2, char pos3)
{//如果只有一个盘子，只需要将盘子从起始位置移动到目的位置上if (n == 1){move(pos1, pos3);}//如果有n(n>=2)个盘子，则需要将n个盘子通过中转位置移动到目的位置上else{//将n-1个盘子通过中转位置移动到目的位置上Hanoi(n - 1, pos1, pos3, pos2);//将第n个移动到目的位置上move(pos1, pos3);//将n-1个盘子通过中转位置移动到目的位置上Hanoi(n - 1, pos2, pos1, pos3);}
}
int main()
{Hanoi(1, 'A', 'B', 'C');printf("\n");Hanoi(2, 'A', 'B', 'C');printf("\n");Hanoi(3, 'A', 'B', 'C');printf("\n");return 0;
}

4.3 完整代码

void move(char pos1, char pos2)
{printf(" %c->%c ", pos1, pos2);
}
//     n:盘子个数 pos1:起始位置 pos2:中转位置 pos3:最终位置
void Hanoi(int n, char pos1, char pos2, char pos3)
{//如果只有一个盘子，只需要将盘子从起始位置移动到目的位置上if (n == 1){move(pos1, pos3);}//如果有n(n>=2)个盘子，则需要将n个盘子通过中转位置移动到目的位置上else{//将n-1个盘子通过中转位置移动到目的位置上Hanoi(n - 1, pos1, pos3, pos2);//将第n个移动到目的位置上move(pos1, pos3);//将n-1个盘子通过中转位置移动到目的位置上Hanoi(n - 1, pos2, pos1, pos3);}
}
int main()
{Hanoi(1, 'A', 'B', 'C');printf("\n");Hanoi(2, 'A', 'B', 'C');printf("\n");Hanoi(3, 'A', 'B', 'C');printf("\n");return 0;
}

4.4 运行结果

答案和我们预想的结果使相同的，通过这样简洁的代码，我们真的解决了汉诺塔问题。

5 总结

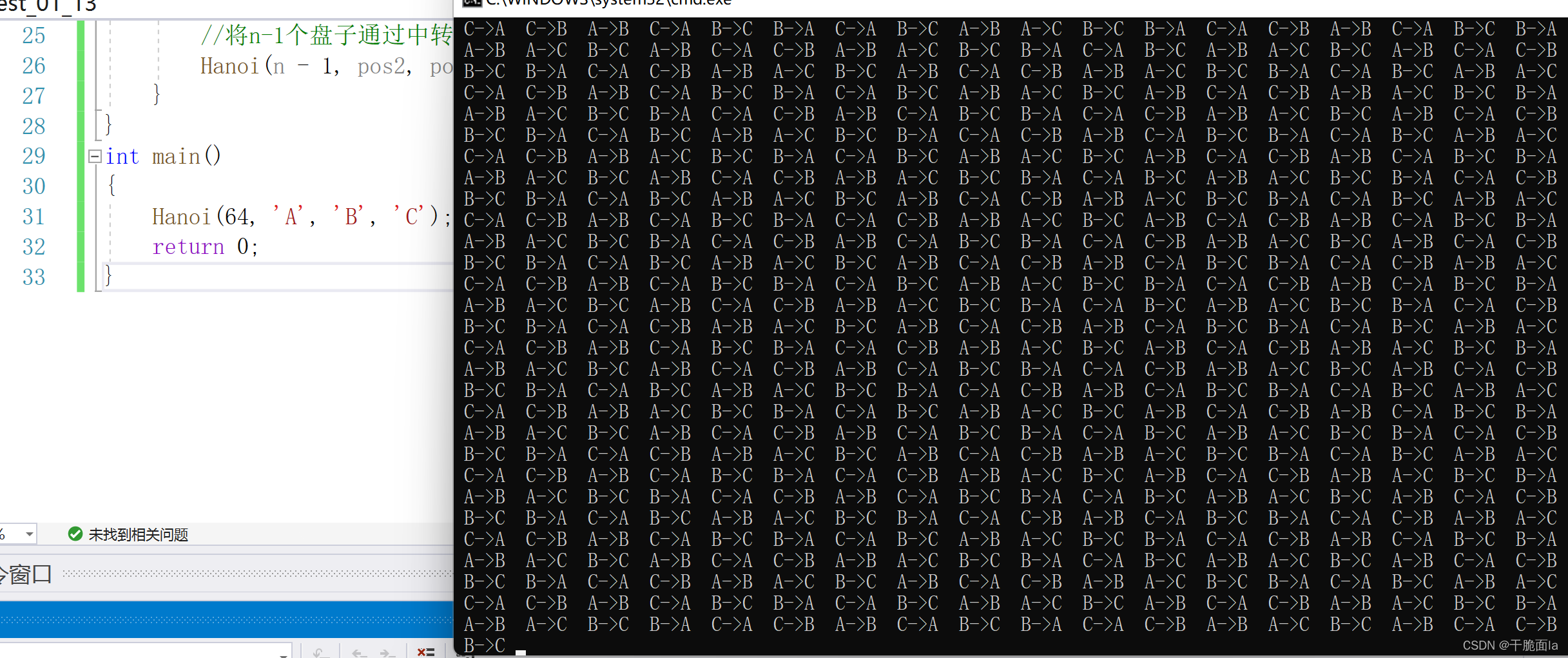
问：当我们把盘子的个数改为64，会发生什么呢？

答：结果是发现我们的程序一直在不停的运行，并打印出密密麻麻的移动过程，原因是64个圆盘的移动实在是太复杂了。

由上面分析我们得知

1个圆盘: A->C 1次：2^1-1
2个圆盘: A->B A->C B->C 3次：2^2-1
3个圆盘: A->C A->B C->B A->C B->A B->C A->C 7次：2^3-1

那么64个圆盘也就是：需要移动2^64-1次，如下图：

假设婆罗门一秒移动一次圆盘，并且在日夜不休的情况下，则需要移动583344215029年。预言说——当这些盘子移动完毕时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽，尘归尘，土归土。

而对于一个普通的计算机来说，要解决64个圆盘的汉诺塔问题也需要耗费上百年的时间，因此才会出现这样的结果。

本次的汉诺塔游戏就讲到这啦~

(完)