背景

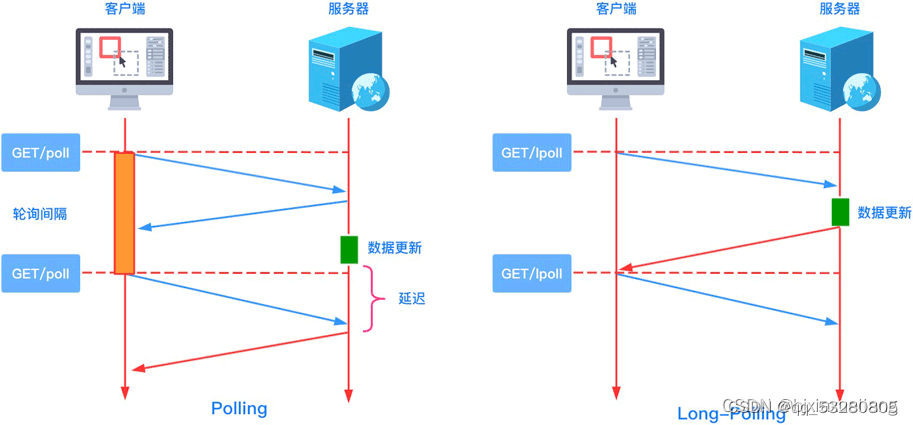
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

分析

(1)当A杆上有一块铜板时，直接将其移动到C杆上即可；

(2)当A杆上有两块铜板时，将较小的那块移动到B杆上，再将较大的那块移动到C杆上（即与(1)相同），最后再将B杆上的那块移动到C杆上即可；

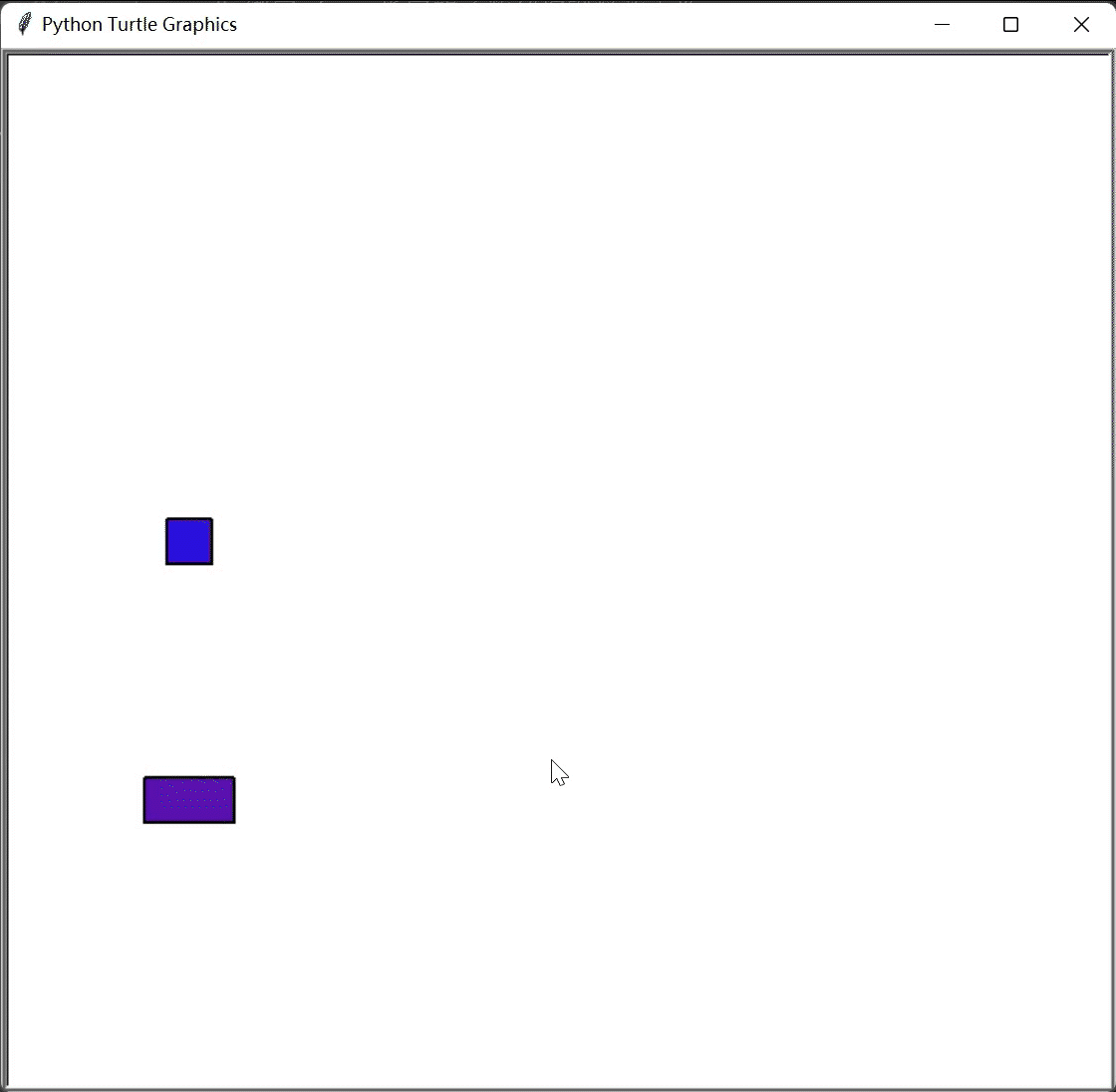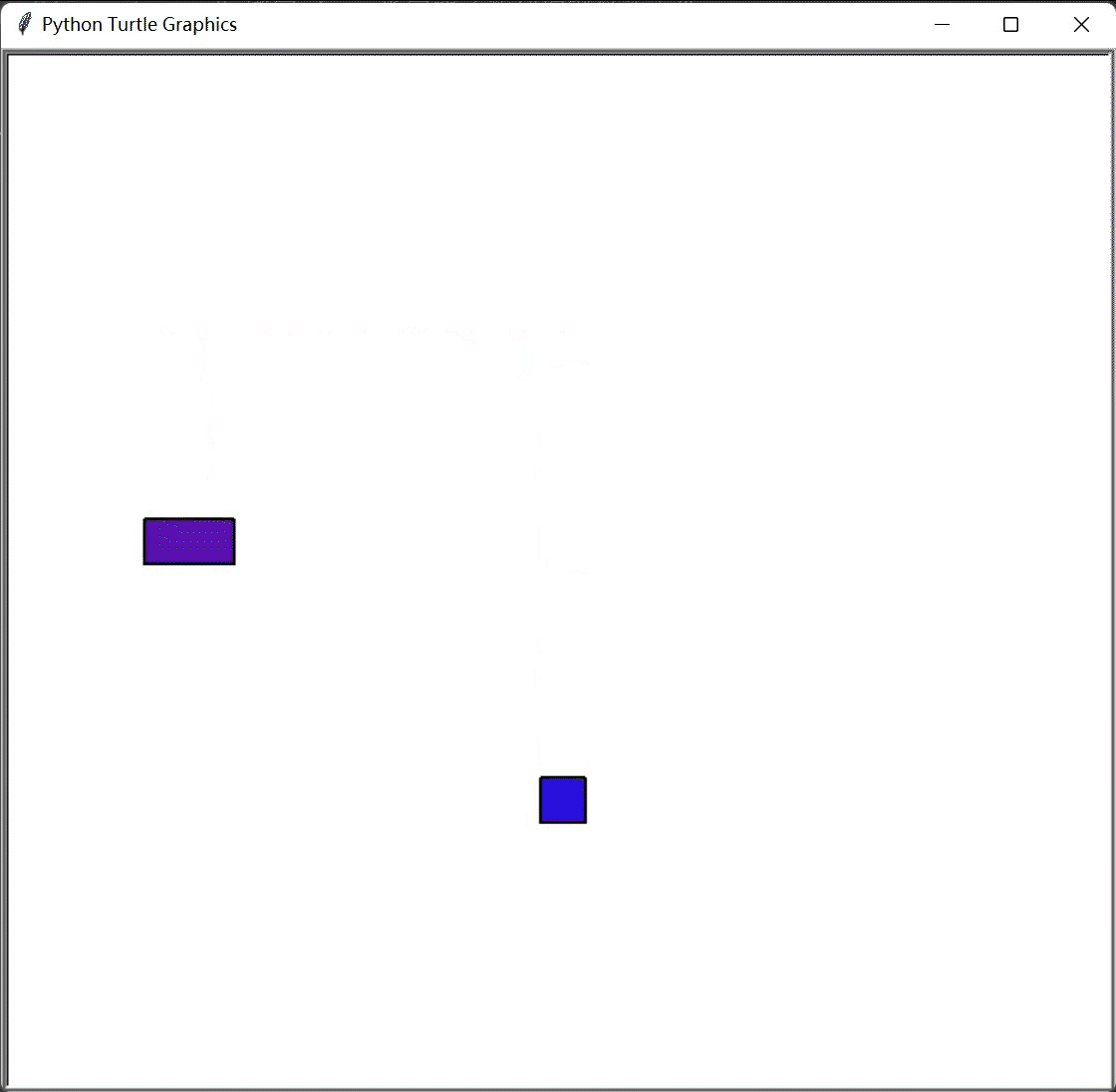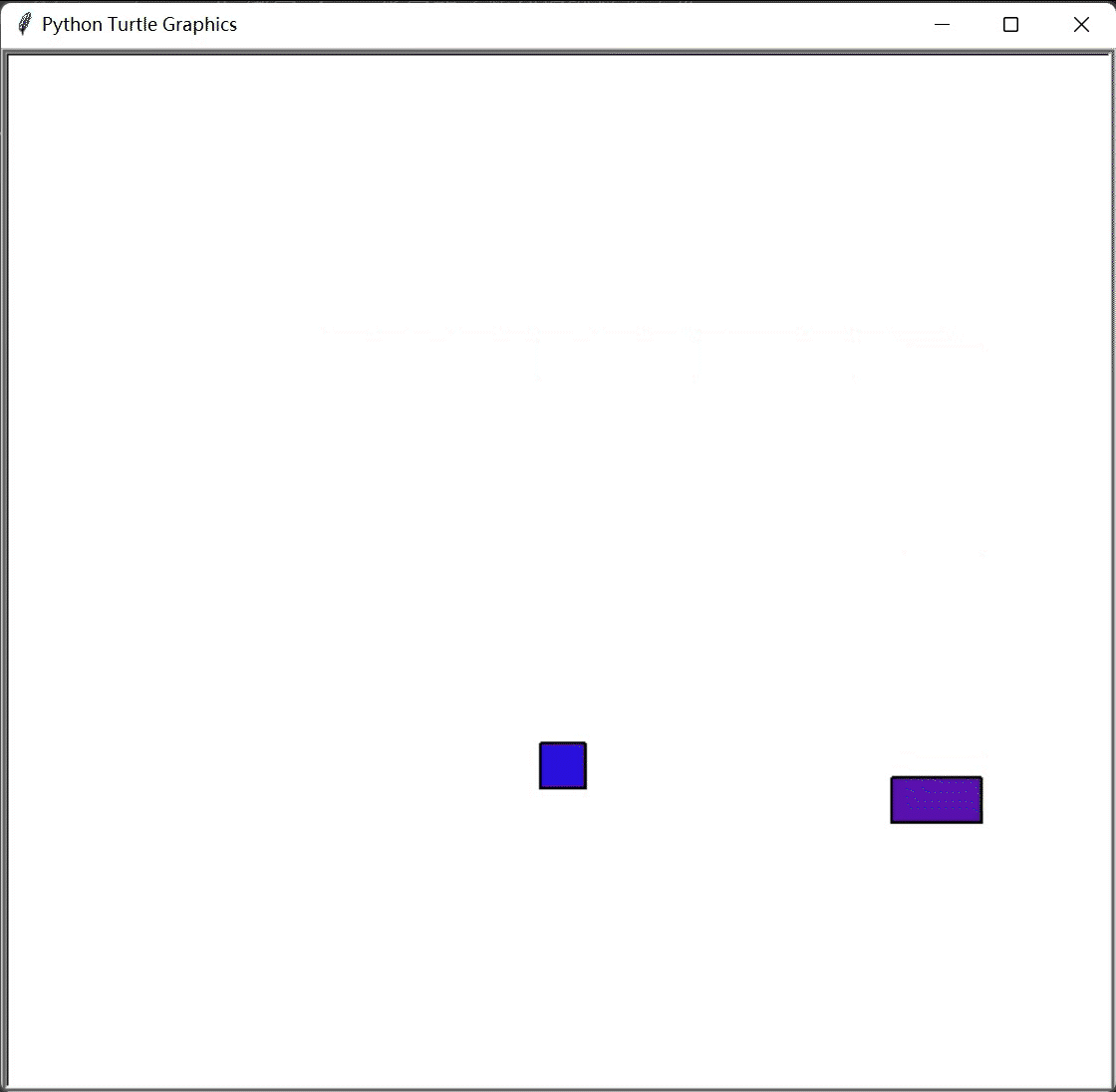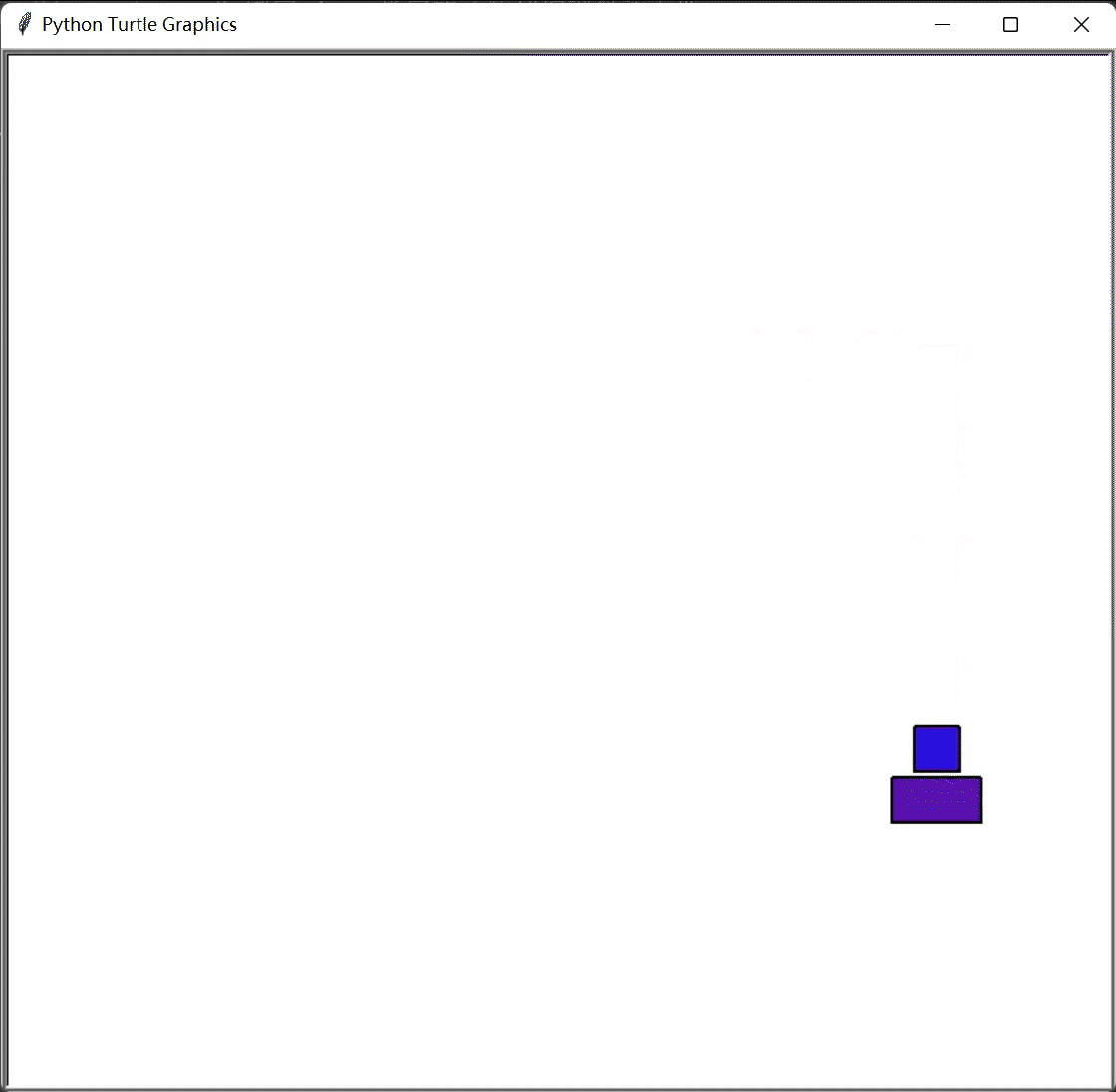
(3)当A杆上有三块铜板时，将A杆上方的两块铜板看成一个整体，要想实现目标，需要将这个整体一起移动到B杆上（即与(2)相同），再将A杆最下方的铜板移动到C杆上，最后再将B杆上的两块铜板移动到C杆上；

…
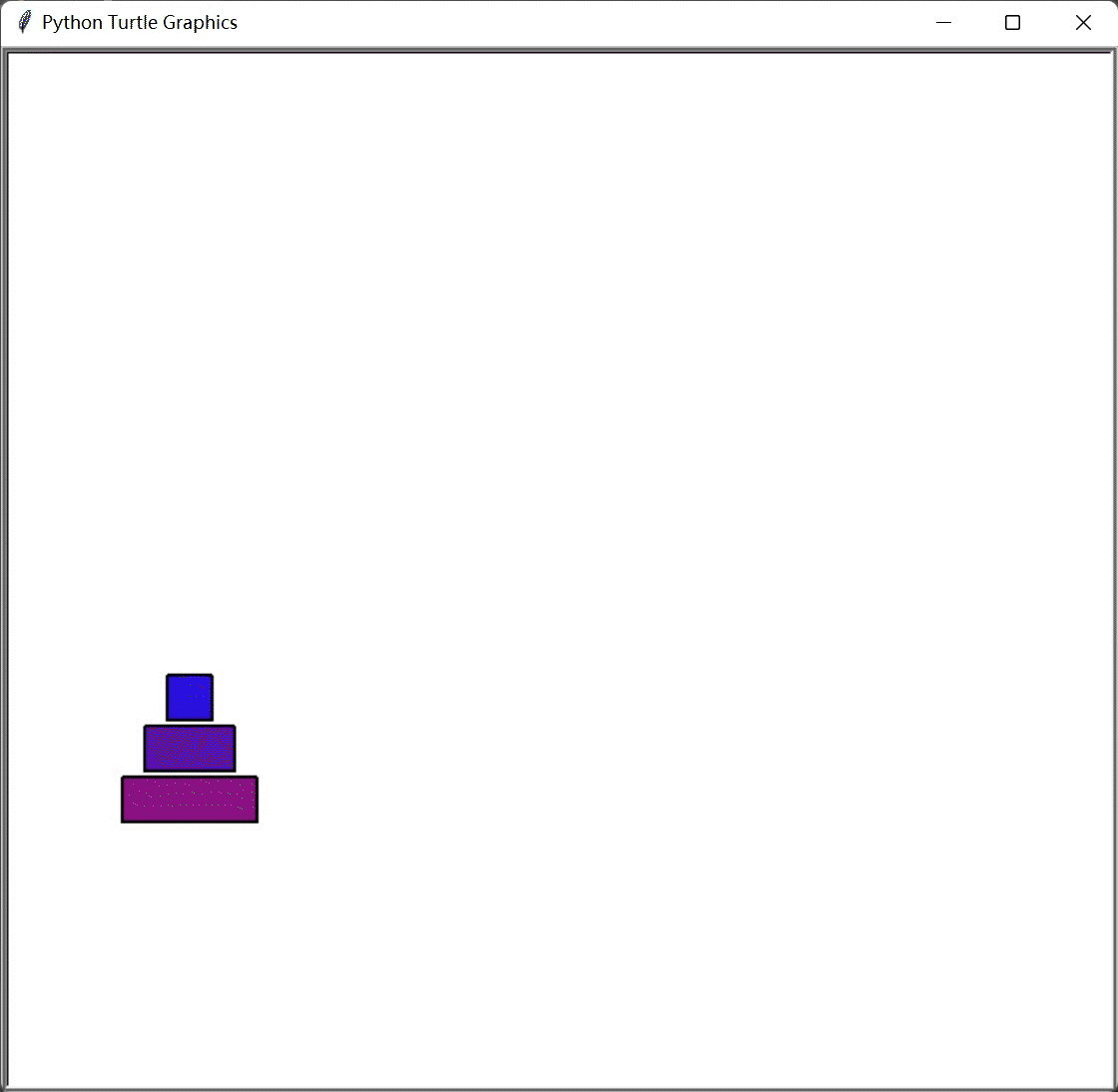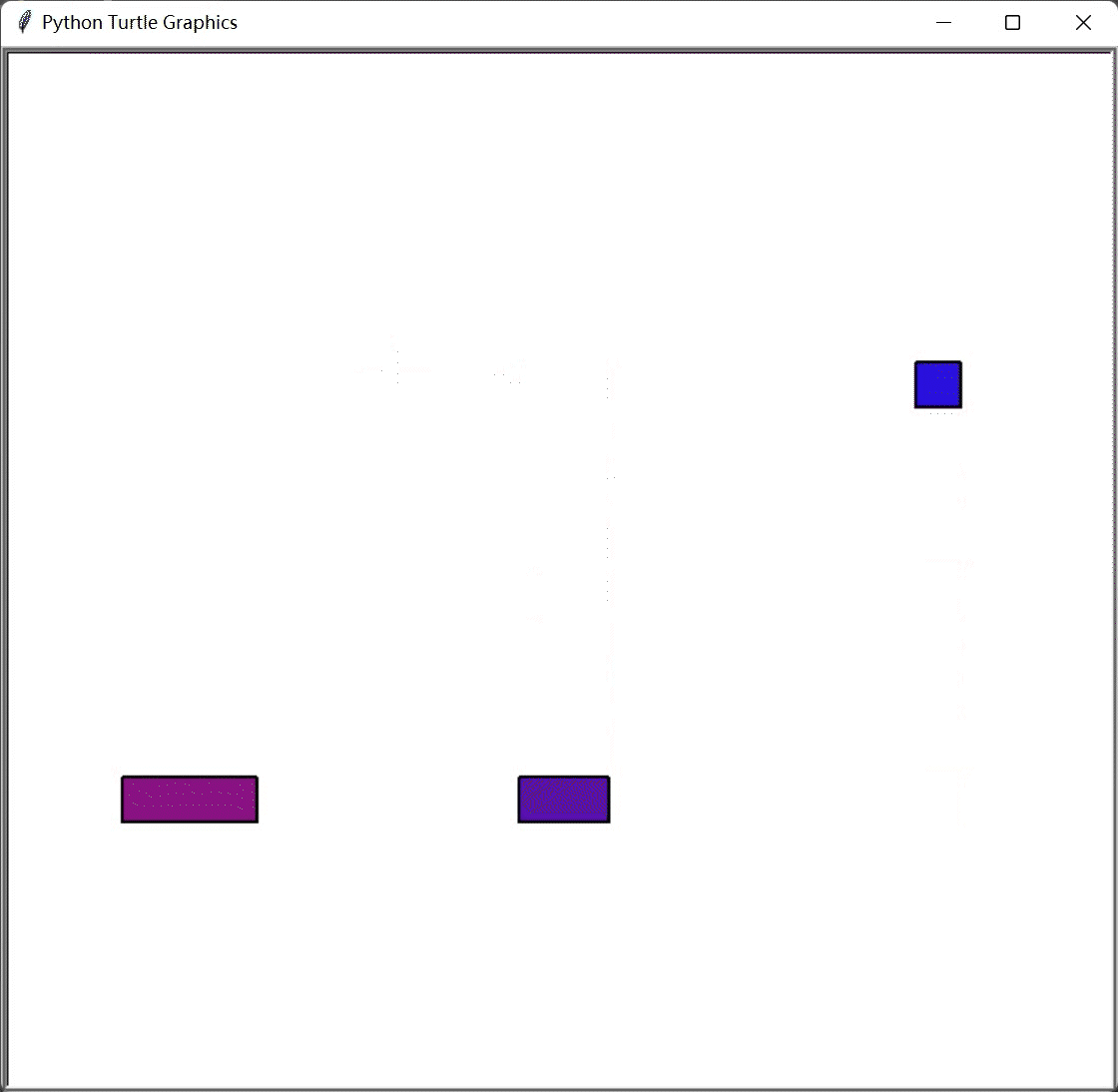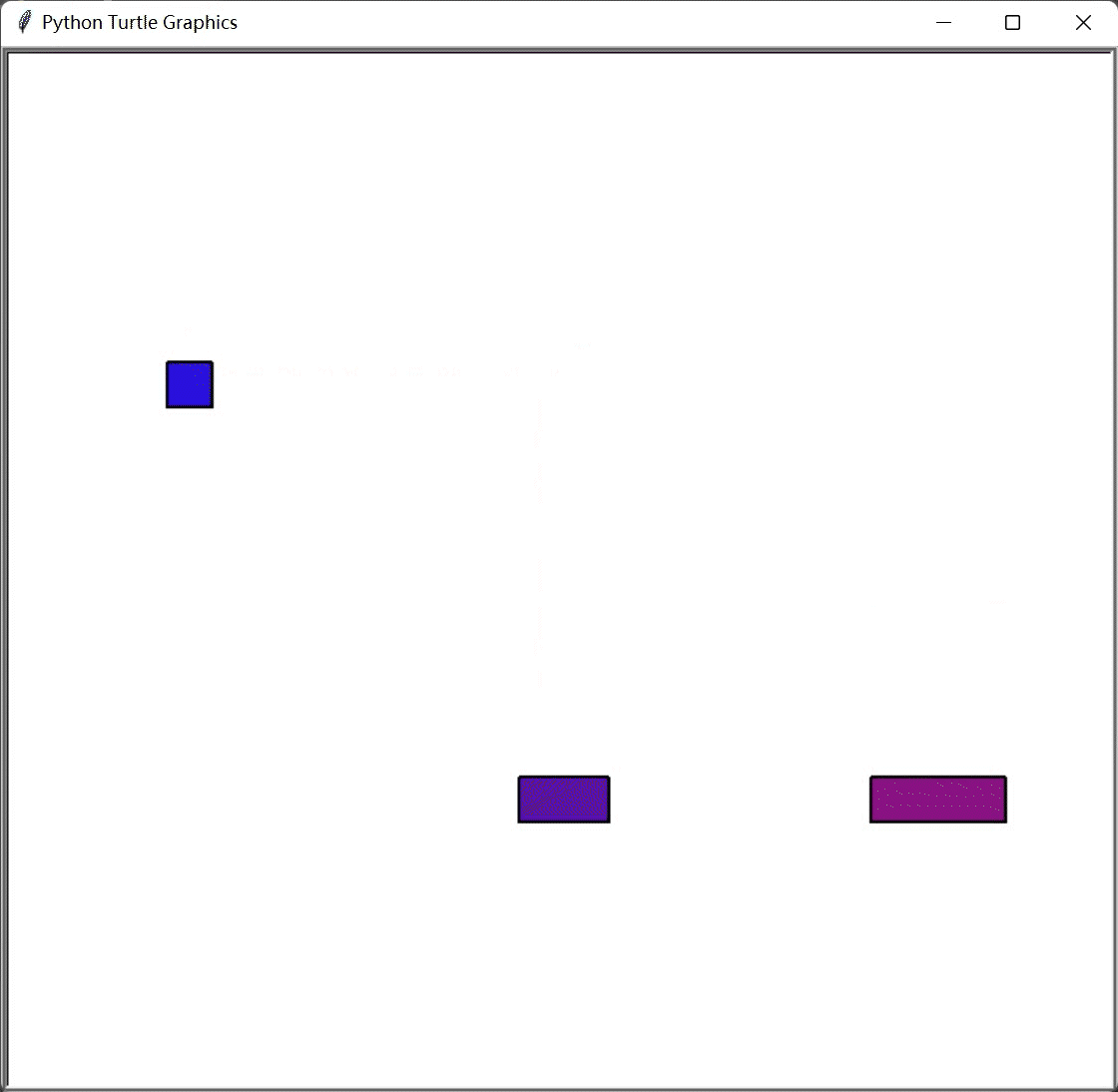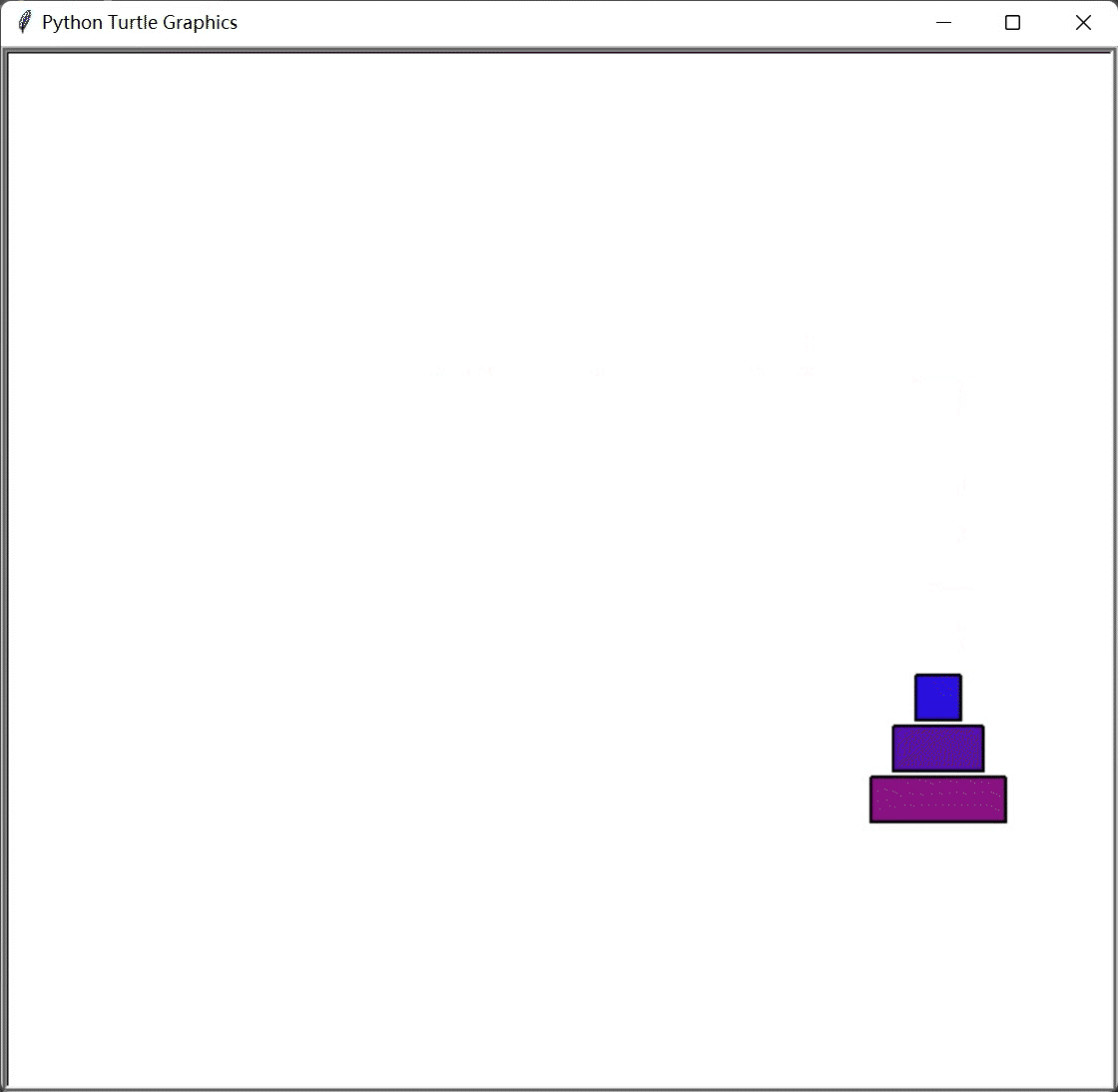
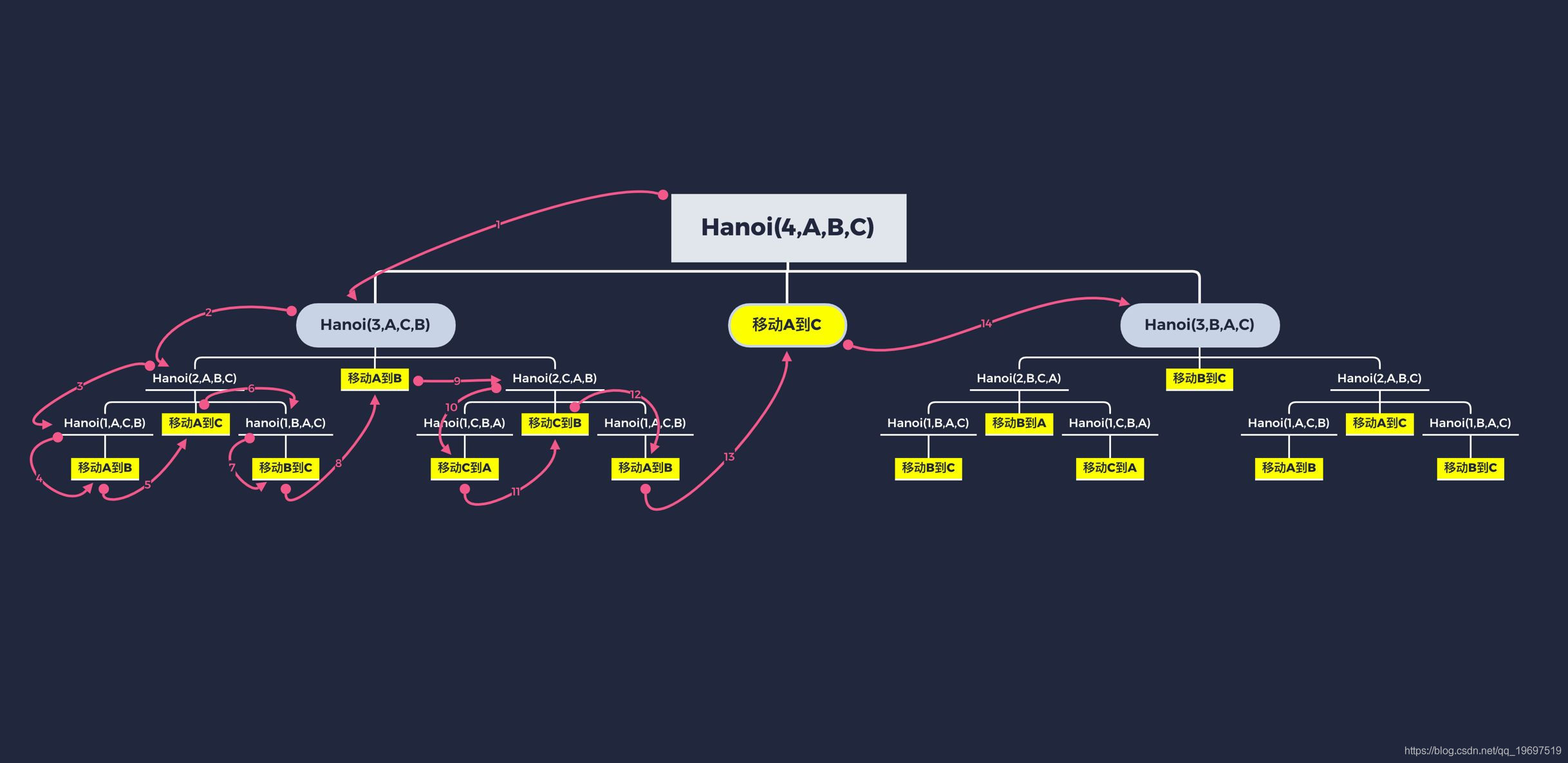
以此类推，当A杆上有n块铜板时，将A杆上方的(n-1)块铜板看成一个整体，一起移动到B杆上，而这就是A杆上有(n-1)块铜板的目标。

假设hanoi(n, from_, with_, to_)是一个函数，表示n块铜板从from_杆上借助于with_杆移动到to_杆上，那么该函数需要实现:
- 将A杆上方(n-1)块铜板借助于C杆移动到B杆，即hanoi(n-1,A,C,B)，调用hanoi()函数自身；
- 将A杆上最后一块铜板移动到C杆,直接移动即可；
- 将B杆上(n-1)块铜板借助于A移动到C杆，即hanoi(n-1,B,A,C)，调用hanoi()函数自身。
这种为了解决问题，重复地将问题分解为同类的子问题的方法就叫递归。

代码实现

python标准库turtle自带汉诺塔例子(${PYTHON_HOME}/Lib/turtledemo/minimal_hanoi.py)，主要递归代码如下：

def hanoi(n, from_, with_, to_):if n > 0:hanoi(n-1, from_, to_, with_)to_.push(from_.pop())hanoi(n-1, with_, from_, to_)

当有6层铜板时，效果如下：