for循环遍历

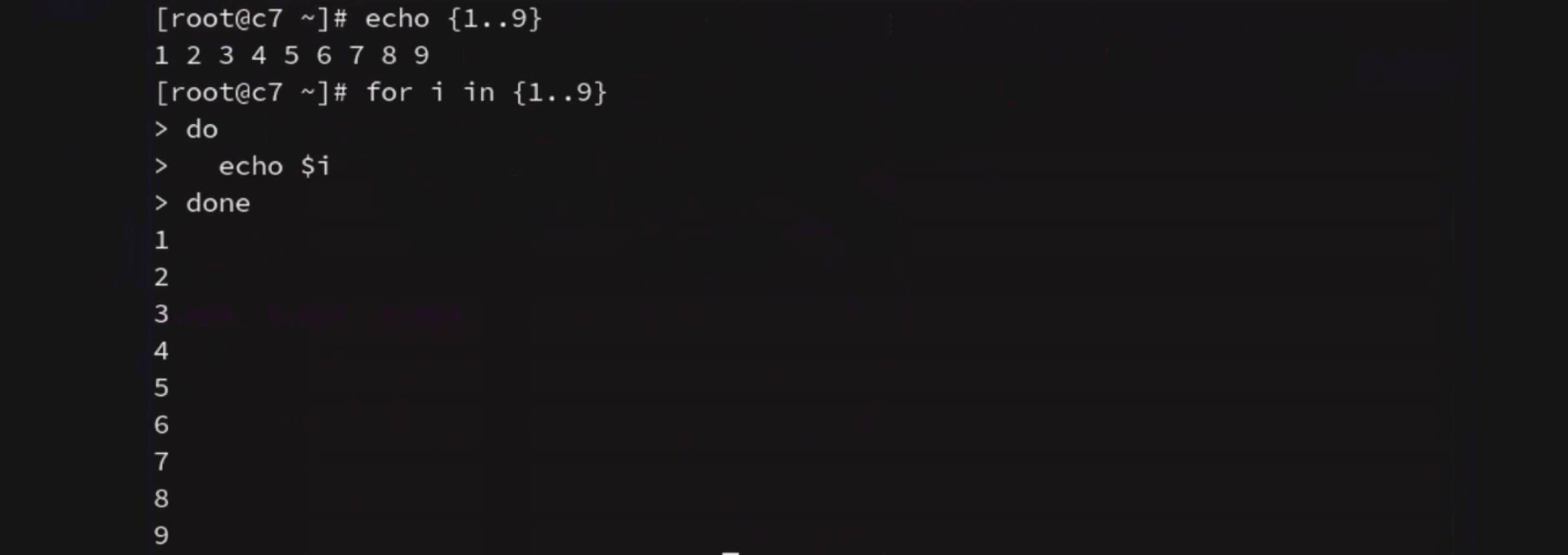
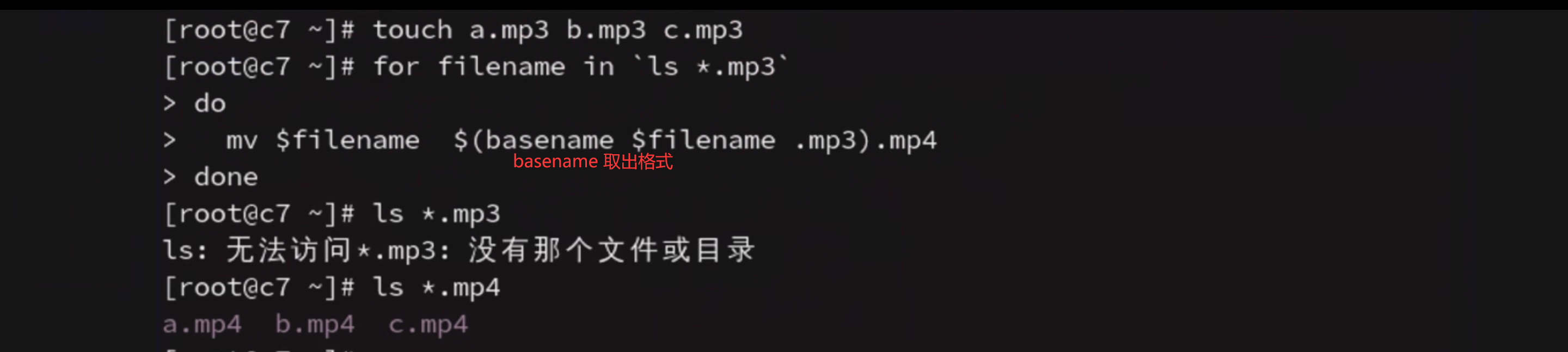
在这里插入图片描述

{ }

在这里插入图片描述

C语言风格的for 遍历

在这里插入图片描述

while 循环

while test测试成立
do命令  
donewhile :   # 相当于while true

在这里插入图片描述

until循环

与while 循环相反

until 循环
while test测试不成立
do命令
done

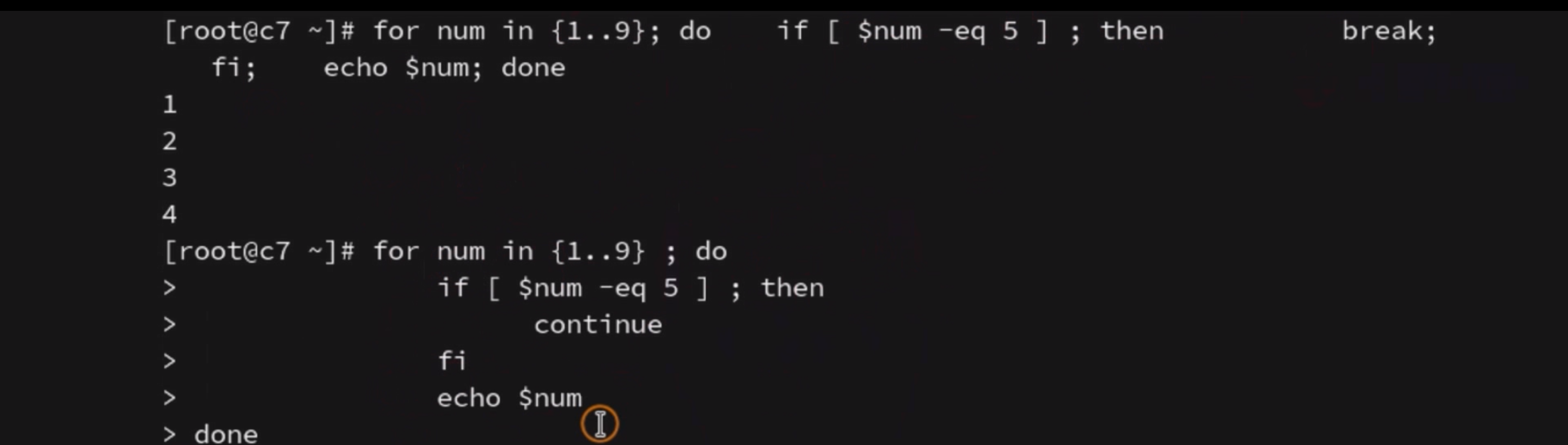
continue & break

在这里插入图片描述

嵌套的时候 if 要和 fi 在一起 do 要和done 在一起 (相邻最近)

九九乘法表双层循环实现

#  echo -n 不换行输出
# echo -e 处理特殊字符
for a int {1..9}
dofor b int {1..9}do [ $b -le $a ] && echo -n "${b}*${a}=$((a*b))"done
done

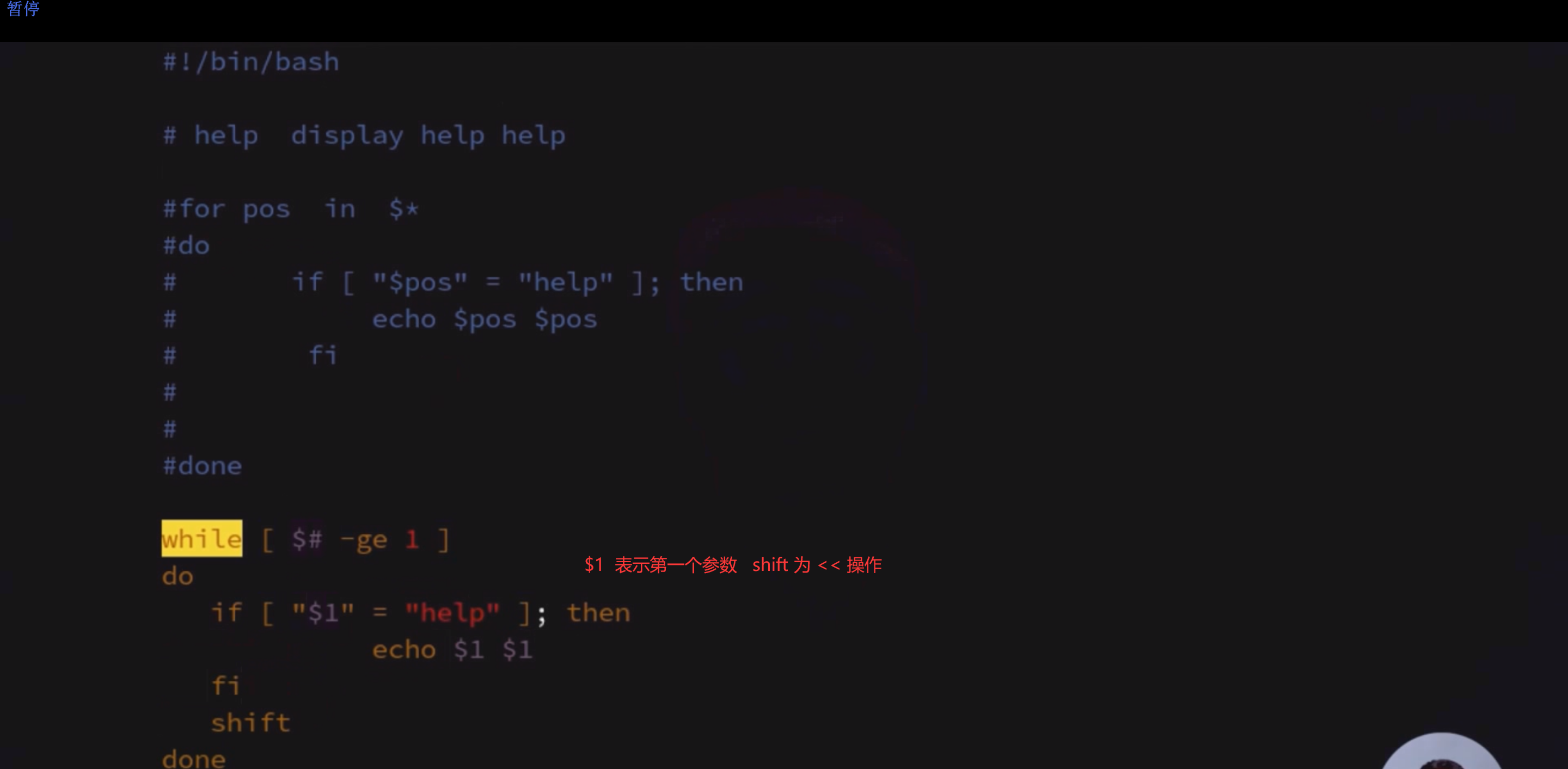
在这里插入图片描述

使用循环处理命令行参数

shift ：参数左移
在这里插入图片描述
vim多行注释 Shift + V 选择行数且是第一个位置然后按Shift + i 输入 # 然后按俩次esc 即可

如果有help 参数就输出俩次
在这里插入图片描述

class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>= 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
};class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>= 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
};
class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>=class Solution {public:int lowbit(int n) {int an = 0;while(n) {if((n & 1) == 1) {an ++;}n >>= 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
};1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
};1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
}; 1;}return an;}vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i ++) {ans.push_back(lowbit(i));}return ans;}
};