目录

1. 前言

2. MDP模型

3. 求解贝尔曼方程

---

1. 前言

        策略评估（Policy Evaluation），简单来说，就是针对某个既定的策略求其状态值函数和动作值函数。求得了状态值函数和动作值函数，事实上就很容易进行不同候补策略之间的性能对比并进而求得最优策略。      

        假定MDP的动力学函数p(s',r|s,a)（或者称迁移函数）是完全知道，理论上来说，就可以针对特定策略的值函数的进行精确的闭式解求解。

2. MDP模型

        本文中的例子取自郭宪，方勇纯《深入浅出强化学习：原理入门》，略有调整。

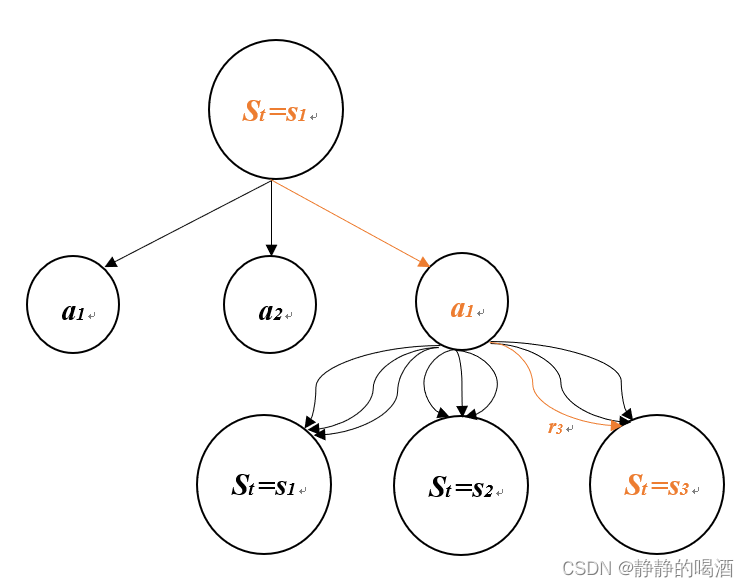
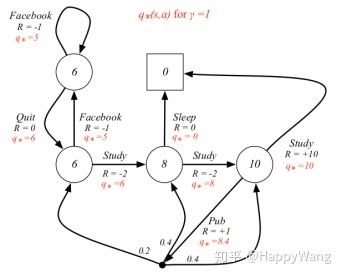
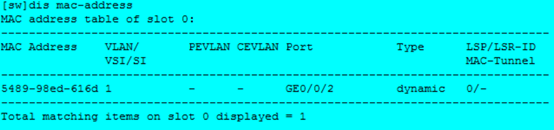
        MDP模型的状态迁移图如下所示：

        这个图事实上包含了MDP模型的所有信息， 动力学函数p(s',r|s,a)和策略可以直接从以上状态转移图中提取出来，如下所示：

        基于以上这些信息，可以精确地求得 的值函数。下一节给出状态值函数的求解示例。

3. 求解贝尔曼方程

        状态值函数的贝尔曼方程如下所示：

        

        将上一节所示的两张表分别代入这个贝尔曼方程，可以得到：

         这就得到了一个4元一次线性方程组。需要注意的是，从以上状态转移图来看，状态5(s5)是终止状态，所以根据定义，它的值函数为0，所以它不是未知数。

        对以上方程组进行整理求解可得：

        当然，以上模型相当简单，所以可以以手算的方式进行求解。如果状态集合、动作集合、奖励集合的大小到了一定的规模后，很快手算求解就成了一件噩梦般的事情了。这是就是借助python或者matlab等内置的线性方程求解工具来进行求解。

        求得了状态值函数，由于动作值函数可以用状态值函数表示，用于基于状态值函数的动作值函数的表示就可以进一步求得动作值函数值。这里就不再赘述。

        进一步，当模型中的各个概率值以及奖励不是明确的数值，而是以符号表示的话，可以利用python或matlab的符号计算功能求解。

        这个基于python和matlab的求解将在后续文章中介绍。参见：强化学习笔记：策略评估--基于numpy的贝尔曼方程数值求解https://chenxiaoyuan.blog.csdn.net/article/details/123258526

回到本系列总目录：强化学习笔记总目录https://chenxiaoyuan.blog.csdn.net/article/details/121715424