强化学习： 贝尔曼方程与马尔可夫决策过程

一、简介

贝尔曼方程和马尔可夫决策过程是强化学习非常重要的两个概念，大部分强化学习算法都是围绕这两个概念进行操作。尤其是贝尔曼方程，对以后理解蒙特卡洛搜索、时序差分算法以及深度强化学习算法都至关重要。这篇文章主要介绍贝尔曼方程。

常用的资料：

《Reinforcement Learning: An Introduction》 author: Richard S.Sutton and Andrew G.Barto

UCL Course: https://www.davidsilver.uk/teaching/

博客园：https://www.cnblogs.com/pinard/

---

二、马尔可夫决策过程

熟悉自然语言处理的同学一定对马尔可夫（Markov）并不陌生，隐马尔科夫模型，条件随机场中都有利用到马尔可夫性质。马尔可夫描述这样一个随机过程：如果一个系统有$N$个状态$S_1,S_2,...,S_N$，随着时间的推移，该系统从某一个状态转移到另一个状态。如果用$q_t$表示系统在时间$t$的状态变量，那么$t$时刻的状态取值为$S_j$的概率取决于前$t-1$个时刻，该概率为：
$$p(q_t=S_j|q_{t-1}=S_i,q_{t-2}=s_k,...)\text{\hspace{1em}(1)}$$
意思很好理解，就是某一时刻状态的取值，取决于前面所有时刻的状态，画图表示为：

那么这个模型猛一看并没有什么问题，我此时此刻的状态是由前面所有时刻的状态所决定的。但是它的致命缺点则是，过于复杂。因为在计算某一个状态的概率时，你需要利用前面所有的状态值，那么多的参数模型肯定复杂。所以马尔可夫模型进行了两个重要的简化：1. 一阶独立性假设。任意一个时刻的状态仅仅依赖于前一个时刻的状态。这个很容易理解，用数学表示为：
$$p(q_t=S_j|q_{t-1}=S_i,q_{t-2}=s_k,...)=p(q_t=S_j|q_{t-1}=S_i)\text{\hspace{1em}(2)}$$
画图表示为：

这样一看，模型就简化很多了，虽然可能会带来模型上的误差，但相比较于难以计算的复杂度，这点误差还是可以接受的。2. 时间独立性假设。可以设想这么一个情况，如果时刻$j$和时刻$j+1$的状态是$a$和$b$，在$i$和$i+1$时刻的状态也分别是$a$和$b$，那么时间独立性可以表示为：
$$\begin{array}{rl}{p}_1& =p(q_{j+1}=b|q_j=a)\\ p_2& =p(q_{i+1}=b|q_i=a)\\ p_1& =p_2\end{array}\text{\hspace{1em}(3)}$$
也就是只要前一个时刻的状态是$a$，那么后一个时刻的状态是$b$的概率是固定的，此概率和$a$所在的时刻（$i$或者$j$）无关。那么既然和时间是无关的，那么由状态$a$转移到状态$b$的概率就可以写作：
$$p(b|a)\text{\hspace{1em}(4)}$$
从而，我们得到马尔可夫模型，一阶独立性假设和时间独立性假设。

---

三、强化学习中的马尔可夫决策过程

回想一下强化学习中的一个重要概念，概率转化模型，也就是$p_{s{s}^{,}}^a$，代表的是，在状态$s$下，采取动作$a$后，转移到状态$s^{,}$的概率。此变量的定义其实已经暗含了马尔科夫假设：状态$s^{,}$发生的概率仅仅和上一时刻的状态$s$相关。当然，还和动作$a$相关，但这个动作$a$可以看作是环境的输入（想一想条件随机场）。因此，可以用数学表达为：
$$p_{s{s}^{,}}^a=p(s^{,}|s,a)\text{\hspace{1em}(5)}$$
这个假设极大的简化了强化学习的状态转移矩阵。此外，除了马尔可夫假设之外，还有一个比较重要的假设，就是对策略$\pi$的假设，回想一下策略$\pi$的定义，在状态$s$下，agent采取动作$a$的概率，表达为概率形式：
$$\begin{array}{r}\pi (a|s)=p(a|s)\end{array}$$
其实也隐含了一个假设，那就是agent的动作$a$只和状态$s$有关。

---

四、贝尔曼方程

如果要说强化学习中最重要的一个公式，那么非贝尔曼方程莫属了，本文将以图表和公式的形式来解释贝尔曼方程，争取能以一种接近人的思维去解释贝尔曼方程。

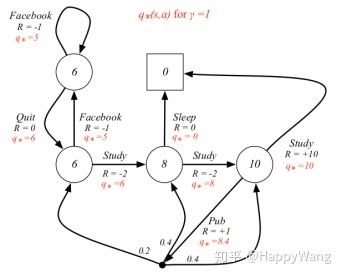
首先引入一个变量，叫做动作价值函数，$q_{\pi }(s,a)$，它的含义是在**状态$s$下，采取动作$a$后所期望获得的总回报。**对比一下价值函数$v_{\pi }(s)$的定义，状态s下，期望获得的总回报，显然，二者的区别在于动作价值函数在状态$s$下多了一个动作$a$的限制。言语无法解释，直接上图：

假设agent初始状态为$A$，在$t=1$时刻，采取了动作$a_{11}$(其他可能的动作$a_{12},a_{13}$)，那么之后可能发生的状态都如红框中所示，而动作价值函数$q_{\pi }(s,a)$代表的就是红框中所能获得回报期望，也就是状态$A$到达所有红框中叶子节点（终点）的回报期望值。从上节的定义中可知，价值函数$v_{\pi }(s)$代表从状态$s$到达所有叶子节点的总回报的期望，因此可以看出来，**动作价值函数只是价值函数的一部分。**那么怎么由动作价值函数去获得价值函数呢？看下图：

如图所示，我们可以把整个状态树可以分成三个分支，分别代表执行$a_{11}$产生的动作价值函数$q_{\pi }(A,a_{11})$，执行$a_{12}$产生的动作价值函数$q_{\pi }(A,a_{12})$，和执行$a_{13}$产生的动作价值函数$q_{\pi }(A,a_{13})$。而价值函数$v_{\pi }(A)$由于代表的是$A$到达所有叶子节点的回报的期望，因此，将这三个分支相加不就是总的价值函数了吗？由此可以得到下式
$$v_{\pi }(s)=\pi (a_{11}|A)q_{\pi }(A,a_{11})+\pi (a_{12}|A)q_{\pi }(A,a_{12})+\pi (a_{13}|A)q_{\pi }(A,a_{13})\text{\hspace{1em}(6)}$$
注意由于是求期望，我们还要乘以各自分支发生的概率$\pi (a|s)$。从而，我们得到了第一个重要的公式，也就是关联动作价值函数和价值函数的等式：
$$v_{\pi }(s)=\sum _a\pi (a|s)q_{\pi }(s,a)\text{\hspace{1em}(7)}$$
它代表的是，一个状态的价值函数，由此状态可能发生的动作价值函数构成，也就是一棵树可以由若干个分支构成，每一个分支是由一个动作产生，这个动作的概率由$\pi$决定，此分支的动作价值函数记为$q_{\pi }(s,a)$。

---

• 贝尔曼方程

  首先回想一下三个重要的等式,分别代表价值函数定义，动作价值函数定义，价值函数和动作价值函数的关系：
  $$\begin{array}{rl}{v}_{\pi }(s)& =E_{\pi }(G_t|S_t=s)=E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s)\\ & \\ p_{\pi }(s,a)& =E_{\pi }(G_t|S_t=s,A_t=a)=E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s,A_t=a)\\ & \\ v_{\pi }(s)& =\sum _a\pi (a|s)p_{\pi }(s,a)\end{array}\text{\hspace{1em}(8)}$$
  这三个公式非常重要，在后面的学习中会经常用到，因此一定要理解他们的含义，以及他们在状态树中代表着什么。下面重点讲解一下贝尔曼方程，首先是纯数学推导：
  $$\begin{array}{rl}{v}_{\pi }(s)& =E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s)\\ & =E_{\pi }(R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+{\gamma }^2{R}_{t+4}+...)|S_t=s)\\ & =E_{\pi }(R_{t+1}+\gamma G_{t+1}|S_t=s)\\ & =E_{\pi }(R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s)\end{array}\text{\hspace{1em}(9)}$$
  递推公式还是比较容易理解的，重点在于我们如何去理解这个公式。我们知道，状态$s$选择一个动作后，会转移到另一个状态，其实贝尔曼方程描述的就是这样一个过程：状态$s$的价值，可以由即时奖励和后续状态获得。

如图所示，状态$s$选择一个动作后，可能会转到某一个橘色状态，如果我们知道了橘色状态的价值（橘色节点代表的子树所有叶子节点奖励的总和的期望值），那么我们就不需要知道计算到叶子节点了，因为橘色的状态足以代表叶子节点。从而，贝尔曼方程实际上为我们提供了一个递归的方式求解问题：计算根节点的价值时，不需要遍历整棵树，而只需要利用根节点的子节点价值。这不是递归的典型特点吗？一个大的问题（求解整棵树的价值)可以由子问题去求解（子节点的价值)。同理，我们也可以得到动作价值函数的贝尔曼方程：
$$q_{\pi }(s,a)=E_{\pi }(R_{t+1}+\gamma Q(S_{t+1},A_{t+1})|S_t=s,A_t=a)\text{\hspace{1em}(17)}$$
贝尔曼方程是我们后续动态规划、时序差分算法的基础，一定要理解其中的含义。

---

动作价值函数和价值函数的关系

上文我们提到，一个重要的等式可以揭示价值函数动作价值函数的关系：
$$v_{\pi }(s)=\sum _a\pi (a|s)q_{\pi }(s,a)\text{\hspace{1em}(11)}$$
那么，动作价值函数是否可以利用价值函数去获得呢？上面说到，每一个动作价值函数其实代表树的一个分支，如下图红框所示：

利用贝尔曼方程的思想，这一分支的价值可以由即时奖励和橘色框状态的价值之和构造，同样是一个动态规划的思想，因此我们有：
$$q_{\pi }(A,a_{11})=R_1+\gamma p_{AB}^{a_{11}}{v}_{\pi }(B)+\gamma p_{AC}^{a_{11}}{v}_{\pi }(C)\text{\hspace{1em}(12)}$$
当然，实际计算的过程，我们应该还要向上述一样，考虑状态转移到其他状态的概率，通用的公式则可以表示为：
$$q_{\pi }(s,a)=R_s^a+\sum _{s^{,}}{p}_{s{s}^{,}}^a{v}_{\pi }(s^{,})\text{\hspace{1em}(13)}$$
他代表的含义是：动作价值函数，可以由即时奖励，以及后续状态的价值，加权求和得到，放在树中，其实就是一个动态规划的思想。

那么，既然价值函数可以由动作价值函数得到，动作价值函数也可以由价值函数得到，价值函数能不能通过价值函数得到呢？同理，动作价值函数能不能通过价值函数得到呢？答案当然是可以的：
$$v_{\pi }(s)=\sum _a\pi (a|s)(R_s^a+\gamma \sum _{s^{,}}{p}_{s{s}^{,}}^a{v}_{\pi }(s^{,}))\text{\hspace{1em}(14)}$$
这个其实就是我们将公式(13)代入公式（11）得到的，但是我们不要死记硬背，我们需要去理解。同理，我们可以得到：
$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{,}}{p}_{s{s}^{,}}^a\sum _{a^{,}}\pi (a^{,}|s^{,})q_{\pi }(s^{,},a^{,})\text{\hspace{1em}(15)}$$
是将（11）式代入（13）式得到的结果。

至此我们得到了几个非常重要的公式：
$$\begin{array}{rl}价值函数定义：v_{\pi }(s)& =E_{\pi }(G_t|S_t=s)=E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s)\\ & \\ 动作价值函数定义：p_{\pi }(s,a)& =E_{\pi }(G_t|S_t=s,A_t=a)=E_{\pi }(R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s,A_t=a)\\ & \\ 价值函数贝尔曼方程：v_{\pi }(s)& =E_{\pi }(R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s)\\ & \\ 动作价值函数贝尔曼方程：q_{\pi }(s,a)& =E_{\pi }(R_{t+1}+\gamma Q(S_{t+1},A_{t+1})|S_t=s,A_t=a)\\ & \\ 动作价值函数到价值函数：v_{\pi }(s)& =\sum _a\pi (a|s)p_{\pi }(s,a)\\ & \\ 价值函数到动作价值函数：q_{\pi }(s,a)& =R_s^a+\sum _{s^{,}}{p}_{s{s}^{,}}^a{v}_{\pi }(s^{,})\\ & \\ 价值函数到价值函数：v_{\pi }(s)& =\sum _a\pi (a|s)(R_s^a+\gamma \sum _{s^{,}}{p}_{s{s}^{,}}^a{v}_{\pi }(s^{,}))\\ & \\ 动作价值函数到动作价值函数：q_{\pi }(s,a)& =R_s^a+\gamma \sum _{s^{,}}{p}_{s{s}^{,}}^a\sum _{a^{,}}\pi (a^{,}|s^{,})q_{\pi }(s^{,},a^{,})\end{array}\text{\hspace{1em}(16)}$$

这些公式，我们都可以找到他们的物理含义，都可以找到他们在状态树上的定义，我们一定要理解着去记忆，明白他们数学推导后的物理含义。