前言: 读书《Reinforcement Learning: An Introduction Second Edition》,读到第三章有限马尔科夫决策过程MDP中,提到了贝尔曼方程的理解。一开始我是有点懵逼的,现在看懂了其意思,在这里解释一下。
贝尔曼方程理解
下面讲解
v π ( s ) = E π [ G t ∣ S t = s ] = E π [ R t + 1 + γ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) [ r + γ E π [ G t + 1 ∣ S t + 1 = s ′ ] ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] f o r a l l s ∈ S \begin{aligned} v_\pi (s) = & \mathbb{E}_\pi [G_t | S_t = s] \\ = & \mathbb{E}_{\pi} [R_{t+1} + \gamma G_{t+1} | S_t = s] \\ = & \sum_a \pi(a|s) \sum_{s'} \sum_{r} p(s', r| s,a) \left[ r + \gamma \mathbb{E}_\pi [G_{t+1} | S_{t+1} = s'] \right] \\ = &\sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a)[r + \gamma v_\pi (s')] \quad for \; all \; s \in S \end{aligned} vπ(s)====Eπ[Gt∣St=s]Eπ[Rt+1+γGt+1∣St=s]a∑π(a∣s)s′∑r∑p(s′,r∣s,a)[r+γEπ[Gt+1∣St+1=s′]]a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]foralls∈S
如何推导。
首先,各符号意义:
- 上图中, v π ( s ) v_\pi(s) vπ(s)表示在状态s下的,使用策略集 π \pi π的价值;
- G t G_t Gt就是在当前时刻 t t t所产生的“回报”,在有限时刻中,通常引入折扣率 γ \gamma γ的概念,将 G t G_t Gt定义为 G t = R t + 1 + γ G t + 1 G_t = R_{t+1} + \gamma G_{t+1} Gt=Rt+1+γGt+1,表示下一步对当前决策影响最大,时间越远,影响越小;
- π ( a ∣ s ) \pi(a|s) π(a∣s)是策略,在我看来就是在状态 s s s下选择动作 a a a的概率;
- p ( ) p() p()是状态转移概率, r r r是回报。
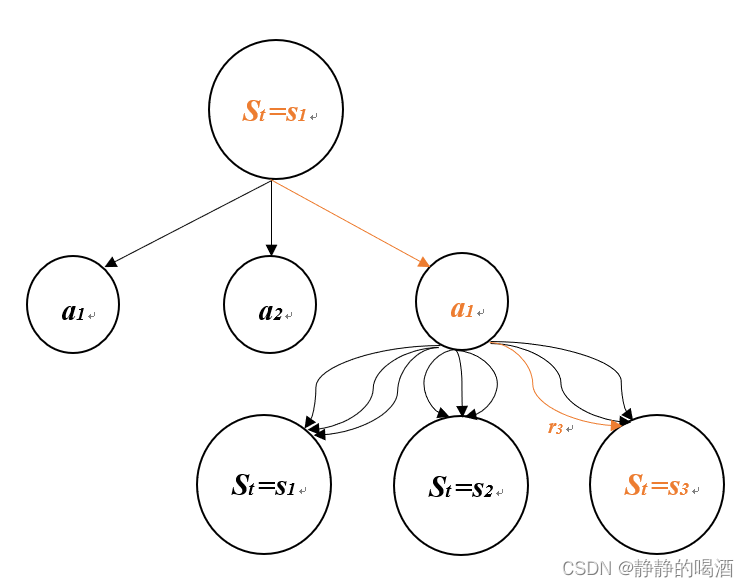
v π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) [ r + γ E π [ G t + 1 ∣ S t + 1 = s ′ ] ] v_\pi(s) = \sum_a \pi(a|s) \sum_{s'} \sum_{r} p(s', r| s,a) \left[ r + \gamma \mathbb{E}_\pi [G_{t+1} | S_{t+1} = s'] \right] vπ(s)=a∑π(a∣s)s′∑r∑p(s′,r∣s,a)[r+γEπ[Gt+1∣St+1=s′]]
上面的公式我有些费解,经过书上的提示,我认为写成下面这样更合适:
v π ( s ) = ∑ a ( π ( a ∣ s ) ∑ s ′ ∑ r ( p ( s ′ , r ∣ s , a ) [ r + γ E π [ G t + 1 ∣ S t + 1 = s ′ ] ] ) ) v_\pi(s) = \sum_a \left( \pi(a|s) \sum_{s'} \sum_{r} \left( p(s', r| s,a) \left[ r + \gamma \mathbb{E}_\pi [G_{t+1} | S_{t+1} = s'] \right] \right) \right) vπ(s)=a∑(π(a∣s)s′∑r∑(p(s′,r∣s,a)[r+γEπ[Gt+1∣St+1=s′]]))

可以通过上图进行理解,在时刻 t t t,其价值即各种选择的期望。而期望即是概率 × \times × 对应事件值,在这里,期望即 该状态 s s s下选择动作 a a a的概率 π ( a ∣ s ) \pi(a|s) π(a∣s) 乘上对应事件,即动作执行后,发生的一系列事件的期望。
贝尔曼方程组
v ( s 1 ) = f ( v ( s 1 ) , v ( s 2 ) , . . . , v ( s n ) ) v ( s 2 ) = f ( v ( s 1 ) , v ( s 2 ) , . . . , v ( s n ) ) . . . v ( s n ) = f ( v ( s 1 ) , v ( s 2 ) , . . . , v ( s n ) ) \begin{aligned} & v(s_1) = f(v(s_1), v(s_2), ..., v(s_n)) \\ & v(s_2) = f(v(s_1), v(s_2), ..., v(s_n)) \\ & ... \\ & v(s_n) = f(v(s_1), v(s_2), ..., v(s_n)) \\ \end{aligned} v(s1)=f(v(s1),v(s2),...,v(sn))v(s2)=f(v(s1),v(s2),...,v(sn))...v(sn)=f(v(s1),v(s2),...,v(sn))
可见,这构造了一个关于 v ( s i ) v(s_i) v(si)的n元1次方程组,可以求解每个状态的价值。
当然,这里 v π ( s ) v_\pi (s) vπ(s)简写成了 v ( s ) v(s) v(s),我们知道每个状态的价值是由策略决定的,策略糟糕,价值低。
贝尔曼最优方程
最优方程说明:最优策略下各个状态的价值一定等于这个状态下最优动作的期望回报。
假设只有2个状态( s 1 s_1 s1与 s 2 s_2 s2),对于状态 s 1 s_1 s1,其最优价值:
v ∗ ( s 1 ) = max { p ( s 1 ∣ s 1 , a 1 ) [ r ( s 1 , a 1 , s 1 ) + γ v ∗ ( s 1 ) ] + p ( s 2 ∣ s 1 , a 1 ) [ r ( s 2 , a 1 , s 1 ) + γ v ∗ ( s 2 ) ] p ( s 1 ∣ s 1 , a 2 ) [ r ( s 1 , a 2 , s 1 ) + γ v ∗ ( s 1 ) ] + p ( s 2 ∣ s 1 , a 2 ) [ r ( s 2 , a 2 , s 1 ) + γ v ∗ ( s 2 ) ] . . . p ( s 1 ∣ s 1 , a n ) [ r ( s 1 , a n , s 1 ) + γ v ∗ ( s 1 ) ] + p ( s 2 ∣ s 1 , a n ) [ r ( s 2 , a n , s 1 ) + γ v ∗ ( s 2 ) ] } v_* (s_1) = \max \left\{ \begin{aligned} & p(s_1 | s_1, a_1) [r(s_1, a_1, s_1) + \gamma v_* (s_1)] + p(s_2 | s_1, a_1) [r(s_2, a_1, s_1) + \gamma v_* (s_2)] \\ & p(s_1 | s_1, a_2) [r(s_1, a_2, s_1) + \gamma v_* (s_1)] + p(s_2 | s_1, a_2) [r(s_2, a_2, s_1) + \gamma v_* (s_2)] \\ & ... \\ & p(s_1 | s_1, a_n) [r(s_1, a_n, s_1) + \gamma v_* (s_1)] + p(s_2 | s_1, a_n) [r(s_2, a_n, s_1) + \gamma v_* (s_2)] \\ \end{aligned} \right\} v∗(s1)=max⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧p(s1∣s1,a1)[r(s1,a1,s1)+γv∗(s1)]+p(s2∣s1,a1)[r(s2,a1,s1)+γv∗(s2)]p(s1∣s1,a2)[r(s1,a2,s1)+γv∗(s1)]+p(s2∣s1,a2)[r(s2,a2,s1)+γv∗(s2)]...p(s1∣s1,an)[r(s1,an,s1)+γv∗(s1)]+p(s2∣s1,an)[r(s2,an,s1)+γv∗(s2)]⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
如上,是需要选择出一个/多个最优动作的。
如果将两个状态的方程式联立,则计算量急剧增大。
而对于状态多的更不用说,几乎不可计算。因此,要使用近似算。