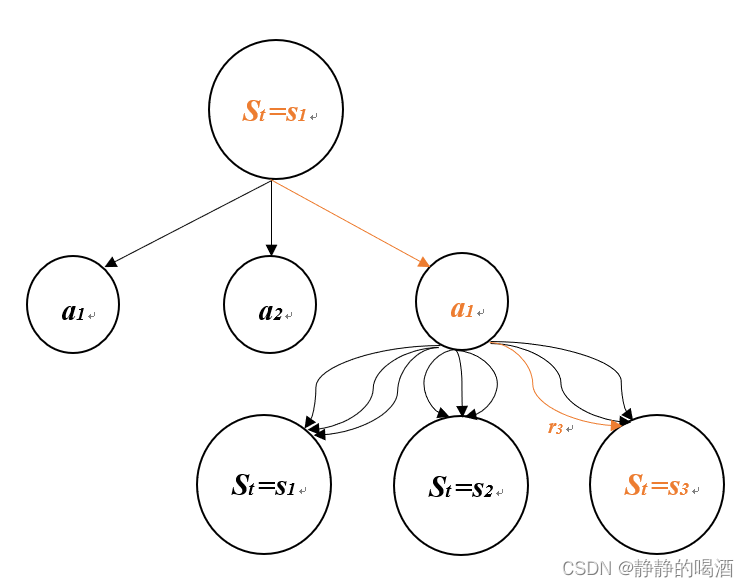
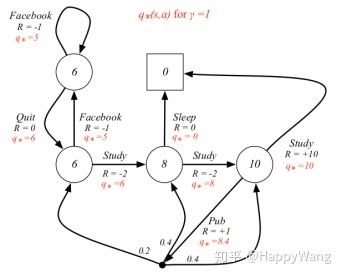
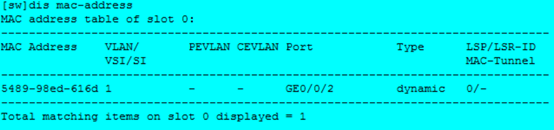
假设智能体观测到状态$s_0$，并且有$N$个可用action，每个action都会导致另一种状态，及相应的奖励。另外，假设我们知道与状态s0相连的所有状态的价值$V_i$。在这种情况下，智能体可以采取的最佳行动是什么？

如果选择动作$a_i$，价值为$V_0(a=a_i)=r_i+V_i$，如果要选择最佳动作，既要保证$a_i$满足$V_0={\max }_{a\in 1,\cdots ,N}(r_a+V_a)$，如果考虑折扣因子的话就变成
$$V_0=\underset{a\in 1,\cdots ,N}{\max }(r_a+\gamma V_a)$$
这个式子就是贝尔曼方程。

在此基础上，我们给环境加入一点不确定性，即，智能体执行action之后对环境产生的影响是不确定的，结果按照某种概率分布给出。

在这个例子中，智能体执行动作$a=1$后导致概率不同的三种结果，这时候价值计算就变成：
$$V_0(a=1)=p_1(r_1+\gamma V_1)+p_2(r_2+\gamma V_2)+p_3(r_3+\gamma V_3)$$
用数学语言表述为
$$V_0\left(a\right)={\mathbb{E}}_{s\sim S}\left[r_{s,a}+\gamma V_s\right]=\sum _{s\in S}{p}_{a,0\to s}\left(r_{s,a}+\gamma V_s\right)$$

式中$p_{a,i\to j}$表示从状态$i$采取动作$a$转移到状态$j$的概率

同时我们考虑贝尔曼方程，就得到了一般情况下的贝尔曼最优方程
$$V_0=\underset{a\in A}{\max }{\mathbb{E}}_{s\sim S}\left[r_{s,a}+\gamma V_s\right]=\underset{a\in A}{\max }\sum _{s\in S}{p}_{a,0\to s}\left(r_{s,a}+\gamma V_s\right)$$