价值函数与贝尔曼方程

article/2025/8/2 22:29:22

一.价值函数

由于在面对不同的状态时，智能体需要选择最优的动作，到达更优的状态以得到更多的奖励.那么我们根据什么判别一个状态或动作的的好坏程度呢？我们引入价值函数。

价值函数的定义是：获得回报的期望。

1.状态价值函数

对于状态来说，状态价值函数 $V_\pi (s)$ 的定义就是：在状态S下智能体能够获得回报的期望值。利用q期望公式定义： $V_\pi(s)=\mathbb{E}[G_t|S_t=s]$ 。其中的角标 $\pi$ 代表计算时按照的是策略 $\pi$ (不同的策略指导下，每个状态的状体价值函数不尽相同，大家可也思考下)。求这个期望的方式有很多种，例如动态规划法，蒙特卡洛法，时间差分法等等。

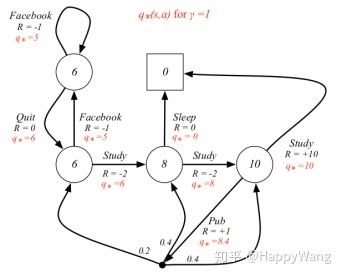
举个例子来说：当我们在状态s的时候，对于未来的动作选择一般呈树状，每个状态作为父节点连接可能的动作，动作又作为父节点连接做出动作之后可能到的状态。但我们之前定义的回报 $G_t$ 只表示树中的一条通路折扣奖励加和，通路很多，计算这个回报可能很困难，在这里我们简化，去除每个“分支”，只保留主干，且省略动作。

假设只有如图几条通路，则我们根据期望的定义式，很容易理解t时刻的状态s，其状态价值函数 $V_\pi(s)$ 就等于转移到每个通路上的概率（由策略决定）乘以每条路上得到的回报即

$V_\pi(s)=\sum p_\pi G_i$ $=0.1\times 100+0.4\times200+0.5\times300=240$

2.动作-状态价值函数（动作价值函数）

类比于状态价值函数，动作-状态价值函数（简称做动作价值函数） $Q_\pi(s,a)$ ,评判的是在某一状态下可选的几种动作的好坏。用期望的形式表示成 $Q_\pi(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$ ,很容易理解。

3.Q-table

知道了状态价值函数与动作价值函数，我们就可以知道：当前状态的好坏，在当前状态下可选择的动作的好坏，我们就可以主动的选择好的动作，到达好的状态。所以我们可以提出一种查表方式的策略。可以定义一个表格（Q_table）来存储不同状态下不同动作的动作价值函数。

Q-table
	a1	a2	a3	...	an
S1	$Q_\pi(s1,a1)$	$Q_\pi(s,a)$	$Q_\pi(s,a)$		$Q_\pi(s,a)$
S2	$Q_\pi(s,a)$	$Q_\pi(s,a)$	$Q_\pi(s,a)$		$Q_\pi(s,a)$
S3	$Q_\pi(s,a)$	$Q_\pi(s,a)$	$Q_\pi(s,a)$		$Q_\pi(s,a)$
...
Sn	$Q_\pi(s,a)$	$Q_\pi(s,a)$	$Q_\pi(s,a)$		$Q_\pi(s,a)$

每当我们观测到当前的状态，就可以在表格中查找状态对应的行，选择动作价值函数最高的动作执行。所以这个输入一个状态，输出一个最佳动作的函数就是策略。更加优秀的做法就是用一个神经网络来拟合表格，我们之后会讲到。

二.贝尔曼方程

将状态-动作-状态的树画出来。我们之前将到过：状态下动作的选择是基于我们的船长——策略，动作执行过后转移到下一个状态的概率分布可以由转移函数描述。既然动作与状态，状态与动作之间存在比较紧密的关系，表征两种优劣程度的价值函数之间也应该有关系，我们分步来看。

1.价值函数之间的关系

我认为，状态价值函数与其叶节点动作价值函数之间的关系很明显，就是一个加权累加，类似于全概率公式。

从数学公式上推导来说，先回顾两个价值函数的定义式：

$V_\pi(s)=\mathbb{E}[G_t|S_t=s]$

$Q_\pi(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$

又因为 $\mathbb{E}[G_t|s,a]=\sum_{a}^{} p_\pi(s,a)\mathbb{E}[G_t|s]$ ,将两个价值函数和策略的定义式分别代替期望式和概率，即得到了等式：

$V_\pi(s)=\sum_{a}\pi(a|s)Q_\pi(s,a)$

类似于上述，在进行动作价值函数与其叶节点的状态价值函数的计算就略显复杂，因为我们在进行完动作进入一个状态时会得到一个奖励，导致需要从回报的定义式出发进行推导，如下：

$\mathbb{E}[G_t|s,a]=\mathbb{E}[R_t+ \gamma R_{t+1}+ \gamma^2 R_{t+2}+...+ \gamma^n R_{t+n}|s,a] =\mathbb{E}[R_t|s,a]+\mathbb{E}[\gamma^2R_{t+1}+...+\gamma^nR_{t+n}|s,a]$

将这个期望的分为两个部分，第一部分是我们获得一步奖励的期望

$\mathbb{E}[R_t|s,a]=\sum_{s}p(s'|s,a)\times r(a)$

剩下的部分 $\mathbb{E}[\gamma^2R_{t+1}+...+\gamma^nR_{t+n}|s,a]$ 中的累加项同时提出一个衰减系数：

$\gamma R_{t+1}+...+\gamma^nR_{t+n}=\gamma(R_{t+1} + ...+ \gamma^{n-1}R_{t+n})=\gamma G_{t+1}$

就是这么神奇，那剩下的部分就变成了 $\mathbb{E}[\gamma G_{t+1}|s,a]=\gamma \mathbb{E}[G_{t+1}|s,a]$

期望式可以由下一时刻状态价值函数根据转移概率权值累加替代，剩下的部分就成为 $\sum_ap(s'|s,a)V_{\pi}(s')$

将前后两部分相加得到： $Q_{\pi}(s,a)=R^a_s+\gamma \sum_ap(s'|s,a)V_{\pi}(s')$ (这里用 $R^a_s$ 代替

一步奖励期望 $\mathbb{E}[R_t|s,a]=\sum_{s}p(s'|s,a)\times r(a)$ 更加简洁）

到此为止，我们就得到了父子节点价值函数的推导关系：

$V_\pi(s)=\sum_{a}\pi(a|s)Q_\pi(s,a)$

$Q_{\pi}(s,a)=R^a_s+\gamma \sum_ap(s'|s,a)V_{\pi}(s')$

若将这段关系进行一次递归处理，我们就可以得到贝尔曼期望方程。

二.贝尔曼期望方程——套娃

刚才我们计算的都是两层之间的，不同种类价值函数之间的关系。如果我们扩展到三层，如下图

那么是否可以求得新的价值函数间的关系？即：同一类价值函数之间的关系。

我们很熟悉前两层的关系： $V_\pi(s)=\sum_{a}\pi(a|s)Q_\pi(s,a)$

我们也很熟悉后两层的关系： $Q_{\pi}(s,a)=R^a_s+\gamma \sum_ap(s'|s,a)V_{\pi}(s')$

那么，如果将第二层关于 $Q_{\pi}(s,a)$ 的等式代入第一个，那么不就很自然的消除了动作价值函数。

得到后继状态 $S'$ 的状态价值函数 $V_{\pi}(S')$ 与当前状态 $S$ 的状态价值函数 $V_{\pi}(S)$ 之间的关系： $V_{\pi}(s)=\sum_{a}\pi(a|s) \left ( R^a_s+\gamma\sum_sp(s'|s,a)V_{\pi}(s')\right )$