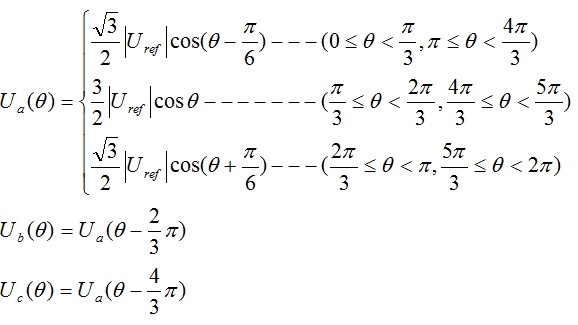1、SVPWM的生成
在FOC矢量控制中,Id、Iq 经过PID输出Vd、Vq。Vd、Vq经过反park变换成Vα、Vβ。再Vα、Vβ合成空间参考矢量Uref。那么怎么根据Vα、Vβ确定Uref所在扇区,然后确定所在扇区两个非零基础矢量的作用时间呢。
1.1、传统的计算方法
1.1.1、扇区的判断
把Uref转换为虚数形式Uref=Va+jVβ。那么其所在扇区 sector = floor(angle(Uref)/(pi/3)) + 1。
1.1.2、两个非零基础矢量的作用时间
那么其所在扇区的两个基础非零矢量的作用时间呢?推导下,假设已确定在第一扇区。

在两相静止参考坐标系(α,β)中,令 Uref 和 U4 间的夹角是 θ,由正弦定理可得:
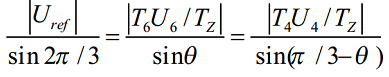
因为 U4 = 2*Udc / 3,所以可以得到两个非零基础矢量的作用时间为
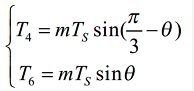
式中 m 为 SVPWM 调制系数(调制比)注意超过1就失真,m=sqrt(3)|Uref|/Udc。可以看出计算两个相邻基础向量的时间需要解三角函数,对单片机来说计算有点费时间。本来一个核心的FOC算法要求在十几二十个微秒内执行完。那么下面介绍一种不需要解三角函数的方法。
1.2、第二种方法
1.2.1、扇区的判断

由Vα、Vβ决定的空间电压矢量所处的扇区。假定合成的电压矢量落在第 I 扇区,可知其等价条件如下:
0° < arctan( Vβ/Vα ) < 60° 以上等价条件再结合矢量图几何关系分析,可以判断出合成电压矢量 Uref
落在第 I 扇区的充分必要条件为:Vα>0、Vβ>0且Vβ/Vα<sqrt(3)。同理可得:

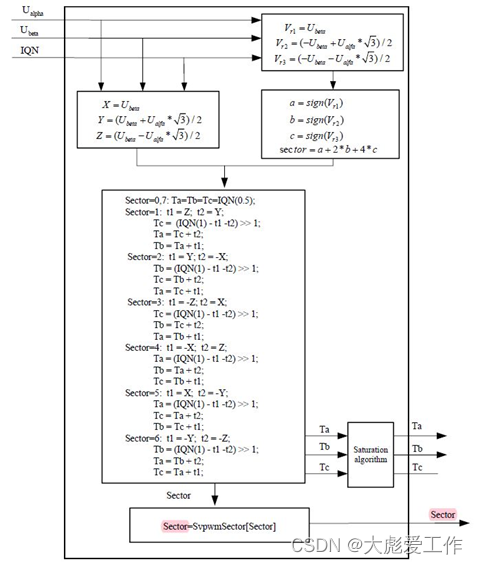
若进一步分析以上的条件,有可看出参考电压矢量 Uref 所在的扇区完全由 U β U_{\beta } Uβ、 3 U α − U β \sqrt{3}U_{\alpha }-U_{\beta} 3Uα−Uβ、 − 3 U α − U β -\sqrt{3}U_{\alpha }-U_{\beta} −3Uα−Uβ 三式决定,因此令:
{ U 1 = U β U 2 = 3 2 U α − 1 2 U β U 3 = − 3 2 U α − 1 2 U β \begin{matrix} \left\{ \begin{aligned} &U_{1}=U_{\beta}\\ &U_{2}=\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta}\\ &U_{3}=-\frac{\sqrt{3}}{2}U_{\alpha}-\frac{1}{2}U_{\beta}\\ \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧U1=UβU2=23Uα−21UβU3=−23Uα−21Uβ
再定义,若U1 > 0 ,则 A=1,否则 A=0;若U 2 > 0 ,则 B=1,否则 B=0;若U3 > 0,则 C=1,否则 C=0。
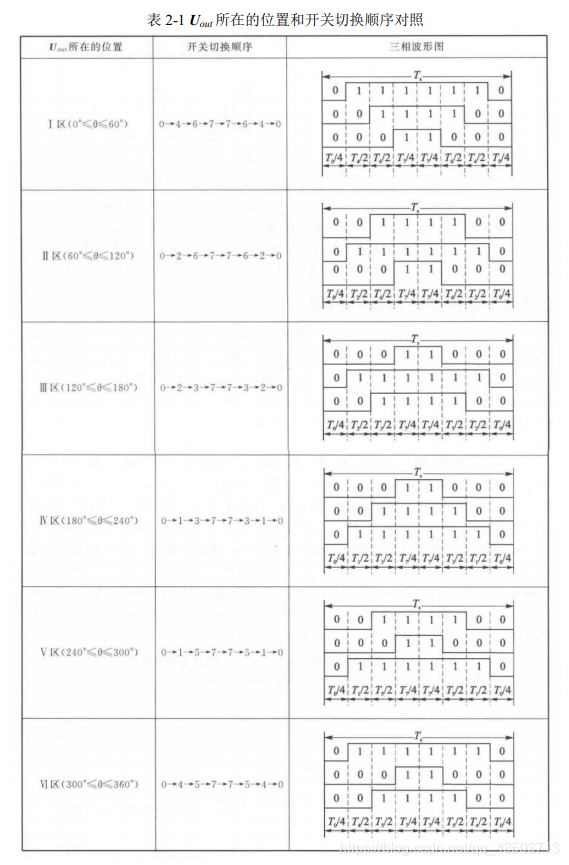
可以看出 A,B,C 之间共有八种组合,但由判断扇区的公式可知 A,B,C不会同时为 1 或同时为 0,所以实际的组合是六种,A,B,C 组合取不同的值对应着不同的扇区,并且是一一对应的,因此完全可以由 A,B,C 的组合判断所在的扇区。为区别六种状态,令 N=4C+2B+A,则可以通过下表计算参考电压矢量 Uref 所在的扇区。
| N | 3 | 1 | 5 | 4 | 6 | 2 |
|---|---|---|---|---|---|---|
| 扇区号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
所以只要简单的逻辑运算就可以确定所在扇区,对于提高系统的响应速度和进行仿真都是很有意义的。
1.2.2、两个非零基础矢量的作用时间
根据伏秒平衡原理,以 Uref 处在第Ⅰ扇区时进行分析,根据图 2-9 有:
假设,电压参考矢量Uref在Uα、Uβ坐标轴上的投影为Uα、Uβ,Uref在两个相邻的非零基础矢量上的投影为 2 3 U d c T 4 T s \frac{2}{3}U_{dc} \frac{T4}{Ts} 32UdcTsT4 、 2 3 U d c T 6 T s \frac{2}{3}U_{dc} \frac{T6}{Ts} 32UdcTsT6,如果Uref在U4、U6上的投影再投影到Uα、Uβ坐标系上,则:
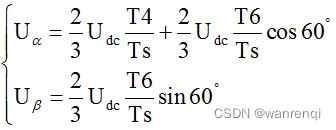
经过整理后得出:
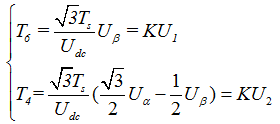
表中两个非零矢量作用时间的比例系数为 K = 3 T s / U d c \sqrt{3}T_{s}/U_{dc} 3Ts/Udc,注意Uref的幅值不能大于 U d c / 3 U_{dc}/\sqrt{3} Udc/3防止Uref在正六边形内切圆外面失真。
如果Uref 处在第II扇区,根据图 2-10 有:
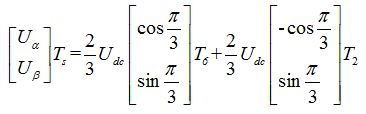
经过整理后得出:
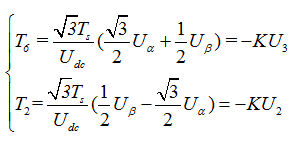
同理可求得Uref在其它扇区中各矢量的作用时间,结果如表2-4所示。
| 扇区 | 时间 |
|---|---|
| Ⅰ | T 4 = K U 2 、 T 6 = K U 1 T_{4}=KU_{2}、T_{6}=KU_{1} T4=KU2、T6=KU1 |
| Ⅱ | T 2 = − K U 2 、 T 6 = − K U 3 T_{2}=-KU_{2}、T_{6}=-KU_{3} T2=−KU2、T6=−KU3 |
| Ⅲ | T 2 = K U 1 、 T 3 = K U 3 T_{2}=KU_{1}、T_{3}=KU_{3} T2=KU1、T3=KU3 |
| Ⅳ | T 1 = − K U 1 、 T 3 = − K U 2 T_{1}=-KU_{1}、T_{3}=-KU_{2} T1=−KU1、T3=−KU2 |
| Ⅴ | T 1 = K U 3 、 T 5 = K U 2 T_{1}=KU_{3}、T_{5}=KU_{2} T1=KU3、T5=KU2 |
| Ⅵ | T 4 = − K U 3 、 T 5 = − K U 1 T_{4}=-KU_{3}、T_{5}=-KU_{1} T4=−KU3、T5=−KU1 |
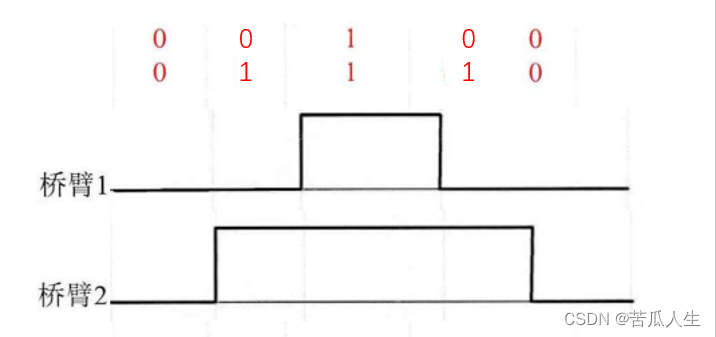
1.1.3、三相占空比的计算
所在扇区的非零基础矢量作用时间已确定了,那么怎么计算各相占空比呢。
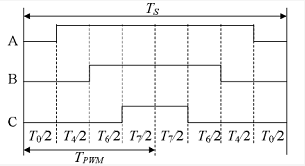
上图为在第一扇区时各相占空比。
{ T a = ( T s − T 4 − T 6 ) / 4 T b = T a + 1 2 T 4 T c = T b + 1 2 T 6 \begin{matrix} \left\{ \begin{aligned} &T_{a}=(T_{s}-T_{4}-T_{6})/4\\ &T_{b}=T_{a}+\frac{1}{2}T_{4}\\ &T_{c}=T_{b}+\frac{1}{2}T_{6} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Ta=(Ts−T4−T6)/4Tb=Ta+21T4Tc=Tb+21T6
或者
{ T a = ( T s + T 4 + T 6 ) / 4 T b = T a − 1 2 T 4 T c = T b − 1 2 T 6 \begin{matrix} \left\{ \begin{aligned} &T_{a}=(T_{s}+T_{4}+T_{6})/4\\ &T_{b}=T_{a}-\frac{1}{2}T_{4}\\ &T_{c}=T_{b}-\frac{1}{2}T_{6} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Ta=(Ts+T4+T6)/4Tb=Ta−21T4Tc=Tb−21T6

上图为在第二扇区时各相占空比。
{ T b = ( T s − T 2 − T 6 ) / 4 T a = T b + 1 2 T 2 T c = T a + 1 2 T 6 \begin{matrix} \left\{ \begin{aligned} &T_{b}=(T_{s}-T_{2}-T_{6})/4\\ &T_{a}=T_{b}+\frac{1}{2}T_{2}\\ &T_{c}=T_{a}+\frac{1}{2}T_{6} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tb=(Ts−T2−T6)/4Ta=Tb+21T2Tc=Ta+21T6
或者
{ T b = ( T s + T 2 + T 6 ) / 4 T a = T b − 1 2 T 2 T c = T a − 1 2 T 6 \begin{matrix} \left\{ \begin{aligned} &T_{b}=(T_{s}+T_{2}+T_{6})/4\\ &T_{a}=T_{b}-\frac{1}{2}T_{2}\\ &T_{c}=T_{a}-\frac{1}{2}T_{6} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tb=(Ts+T2+T6)/4Ta=Tb−21T2Tc=Ta−21T6

上图为在第三扇区时各相占空比。
{ T b = ( T s − T 2 − T 3 ) / 4 T c = T b + 1 2 T 2 T a = T c + 1 2 T 3 \begin{matrix} \left\{ \begin{aligned} &T_{b}=(T_{s}-T_{2}-T_{3})/4\\ &T_{c}=T_{b}+\frac{1}{2}T_{2}\\ &T_{a}=T_{c}+\frac{1}{2}T_{3} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tb=(Ts−T2−T3)/4Tc=Tb+21T2Ta=Tc+21T3
或者
{ T b = ( T s + T 2 + T 3 ) / 4 T c = T b − 1 2 T 2 T a = T c − 1 2 T 3 \begin{matrix} \left\{ \begin{aligned} &T_{b}=(T_{s}+T_{2}+T_{3})/4\\ &T_{c}=T_{b}-\frac{1}{2}T_{2}\\ &T_{a}=T_{c}-\frac{1}{2}T_{3} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tb=(Ts+T2+T3)/4Tc=Tb−21T2Ta=Tc−21T3

上图为在第四扇区时各相占空比。
{ T c = ( T s − T 1 − T 3 ) / 4 T b = T c + 1 2 T 1 T a = T b + 1 2 T 3 \begin{matrix} \left\{ \begin{aligned} &T_{c}=(T_{s}-T_{1}-T_{3})/4\\ &T_{b}=T_{c}+\frac{1}{2}T_{1}\\ &T_{a}=T_{b}+\frac{1}{2}T_{3} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tc=(Ts−T1−T3)/4Tb=Tc+21T1Ta=Tb+21T3
或者
{ T c = ( T s + T 1 + T 3 ) / 4 T b = T c − 1 2 T 1 T a = T b − 1 2 T 3 \begin{matrix} \left\{ \begin{aligned} &T_{c}=(T_{s}+T_{1}+T_{3})/4\\ &T_{b}=T_{c}-\frac{1}{2}T_{1}\\ &T_{a}=T_{b}-\frac{1}{2}T_{3} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tc=(Ts+T1+T3)/4Tb=Tc−21T1Ta=Tb−21T3

上图为在第五扇区时各相占空比。
{ T c = ( T s − T 1 − T 5 ) / 4 T a = T c + 1 2 T 1 T b = T a + 1 2 T 5 \begin{matrix} \left\{ \begin{aligned} &T_{c}=(T_{s}-T_{1}-T_{5})/4\\ &T_{a}=T_{c}+\frac{1}{2}T_{1}\\ &T_{b}=T_{a}+\frac{1}{2}T_{5} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tc=(Ts−T1−T5)/4Ta=Tc+21T1Tb=Ta+21T5
或者
{ T c = ( T s + T 1 + T 5 ) / 4 T a = T c − 1 2 T 1 T b = T a − 1 2 T 5 \begin{matrix} \left\{ \begin{aligned} &T_{c}=(T_{s}+T_{1}+T_{5})/4\\ &T_{a}=T_{c}-\frac{1}{2}T_{1}\\ &T_{b}=T_{a}-\frac{1}{2}T_{5} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Tc=(Ts+T1+T5)/4Ta=Tc−21T1Tb=Ta−21T5

上图为在第六扇区时各相占空比。
{ T a = ( T s − T 4 − T 5 ) / 4 T c = T a + 1 2 T 4 T b = T c + 1 2 T 5 \begin{matrix} \left\{ \begin{aligned} &T_{a}=(T_{s}-T_{4}-T_{5})/4\\ &T_{c}=T_{a}+\frac{1}{2}T_{4}\\ &T_{b}=T_{c}+\frac{1}{2}T_{5} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Ta=(Ts−T4−T5)/4Tc=Ta+21T4Tb=Tc+21T5
或者
{ T a = ( T s + T 4 + T 5 ) / 4 T c = T a − 1 2 T 4 T b = T c − 1 2 T 5 \begin{matrix} \left\{ \begin{aligned} &T_{a}=(T_{s}+T_{4}+T_{5})/4\\ &T_{c}=T_{a}-\frac{1}{2}T_{4}\\ &T_{b}=T_{c}-\frac{1}{2}T_{5} \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧Ta=(Ts+T4+T5)/4Tc=Ta−21T4Tb=Tc−21T5
上式中 T a 、 T b 、 T c 、 T s T_{a}、T_{b}、T_{c}、T_{s} Ta、Tb、Tc、Ts表示A、B,C三相的占空比,和PWM周期。如果把上式写成一个通用的式子。
{ t a = ( T s − T x − T y ) / 4 t b = ( t a + 1 2 T x ) t c = ( t b + 1 2 T y ) \begin{matrix} \left\{ \begin{aligned} &t_{a}=(T_{s}-T_{x}-T_{y})/4\\ &t_{b}=(t_{a}+\frac{1}{2}T_{x})\\ &t_{c}=(t_{b}+\frac{1}{2}T_{y})\\ \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧ta=(Ts−Tx−Ty)/4tb=(ta+21Tx)tc=(tb+21Ty)
或者
{ t a = ( T s + T x + T y ) / 4 t b = ( t a − 1 2 T x ) t c = ( t b − 1 2 T y ) \begin{matrix} \left\{ \begin{aligned} &t_{a}=(T_{s}+T_{x}+T_{y})/4\\ &t_{b}=(t_{a}-\frac{1}{2}T_{x})\\ &t_{c}=(t_{b}-\frac{1}{2}T_{y})\\ \end{aligned} \right. \end{matrix} ⎩ ⎨ ⎧ta=(Ts+Tx+Ty)/4tb=(ta−21Tx)tc=(tb−21Ty)
其中下标 y 大于 x 。ta、tb 和 tc分别是相应的比较器的值,而不同扇区比较器的值分配如表下所示:
| 扇区 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| T a T_{a} Ta | t a t_{a} ta | t b t_{b} tb | t b t_{b} tb | t c t_{c} tc | t c t_{c} tc | t a t_{a} ta |
| T b T_{b} Tb | t b t_{b} tb | t a t_{a} ta | t c t_{c} tc | t b t_{b} tb | t a t_{a} ta | t c t_{c} tc |
| T c T_{c} Tc | t c t_{c} tc | t c t_{c} tc | t a t_{a} ta | t a t_{a} ta | t b t_{b} tb | t b t_{b} tb |
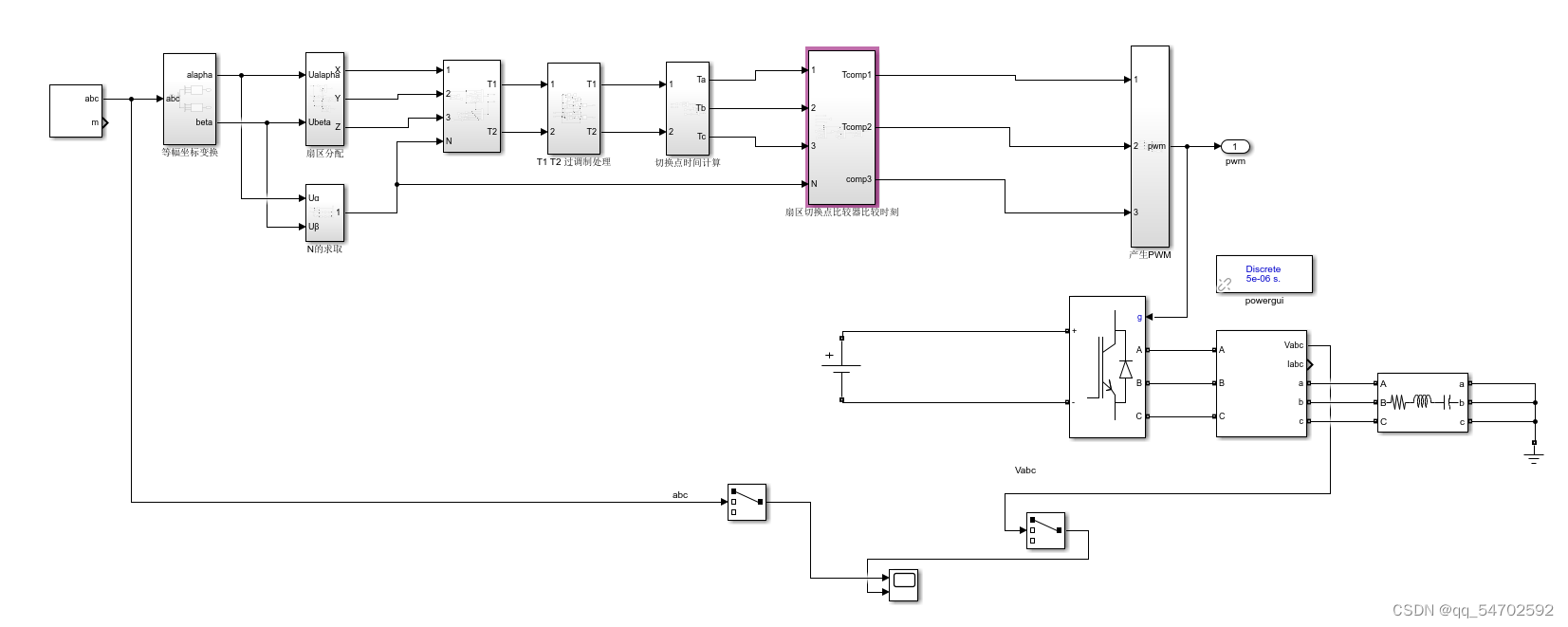
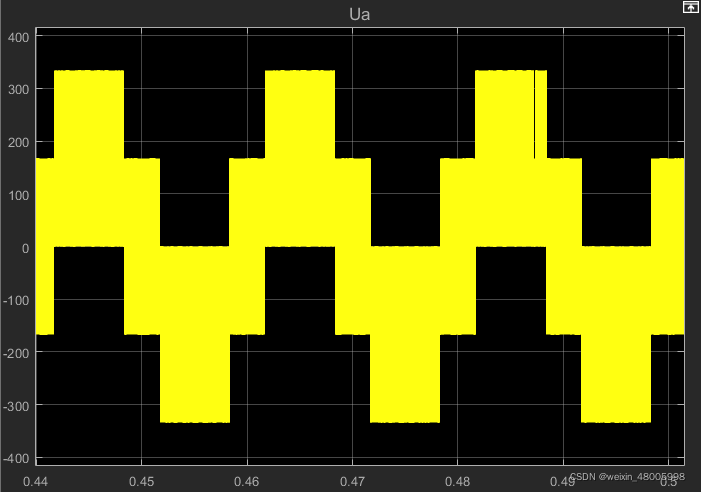
2、SVPWM的simulink仿真
下面根据第二种方法来仿真:
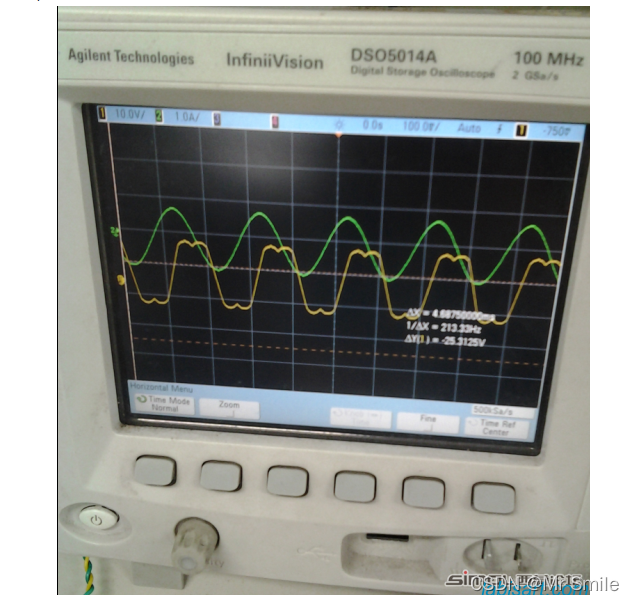
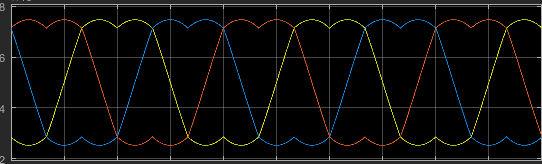
2.1、simulink仿真波形图


2.2、simulink仿真程序
程序中去掉了Udc,然后也限制了过调制失真。
function [Ta,Tb,Tc] = fcn(ua,ub,udc,Ts)u1 = ub;
u2 = sqrt(3)/2*ua - 1/2*ub;
u3 = -sqrt(3)/2*ua - 1/2*ub;if u1 > 0a = 1;
else a = 0;
endif u2 > 0b = 1;
else b = 0;
endif u3 > 0c = 1;
else c = 0;
endN = 4*c + 2*b + a;Ts = Ts*2; %因为PWM是中心对齐模式k = sqrt(3)*Ts/udc; switch Ncase 1 %第2扇区t1 = -k*u2;t2 = -k*u3;Tb = ((Ts)+ t1 + t2)/4; Ta = Tb - t1/2; Tc = Ta - t2/2; case 2 %第6扇区t1=-k*u3;t2=-k*u1;Ta = ((Ts)+ t1 + t2)/4; Tc = Ta - t1/2; Tb = Tc - t2/2; case 3 %第1扇区t1=k*u2;t2=k*u1;Ta = ((Ts)+ t1 + t2)/4; Tb = Ta - t1/2; Tc = Tb - t2/2; case 4 %第4扇区t1=-k*u1;t2=-k*u2;Tc = ((Ts)+ t1 + t2)/4; Tb = Tc - t1/2; Ta = Tb - t2/2; case 5 %第3扇区t1=k*u1;t2=k*u3;Tb = ((Ts)+ t1 + t2)/4; Tc = Tb - t1/2; Ta = Tc - t2/2; case 6 %第5扇区t1=k*u3;t2=k*u2;Tc = ((Ts) + t1 + t2)/4; Ta = Tc - t1/2; Tb = Ta - t2/2; otherwise Ta = Ts/4; Tb = Ts/4; Tc = Ts/4; endend参考模型:https://download.csdn.net/download/wanrenqi/35140354