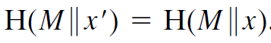​Schnorr协议简介

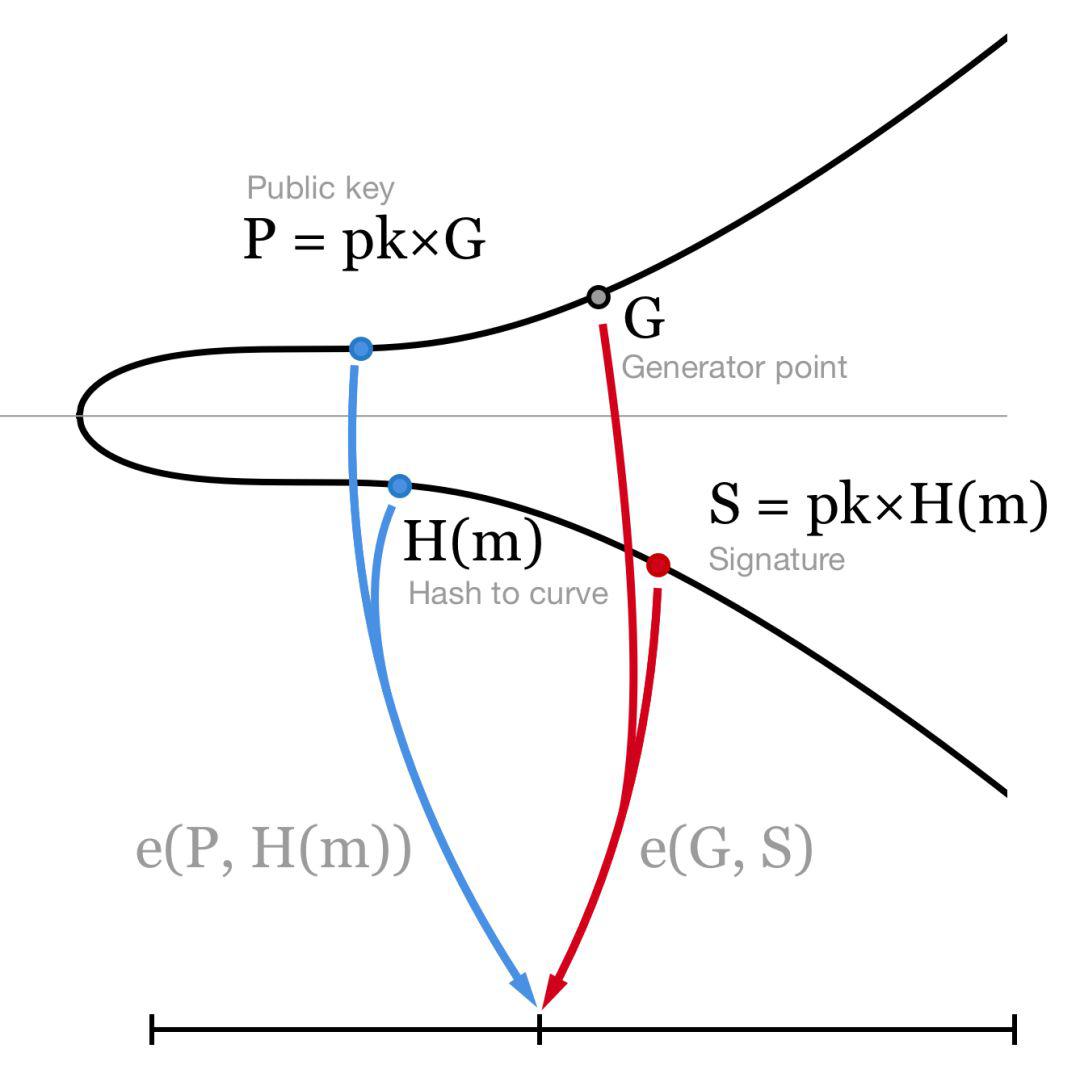
Schnorr协议是由德国数学家和密码学家Claus-Peter Schnorr在1991年提出，是一种基于离散对数难题的知识证明机制。Schnorr本质上是一种零知识的技术，即Prover声称知道一个密钥x的值，通过使用Schnorr加密技术，可以在不揭露x的值情况下向Verifier证明对x的知情权，即可用于证明你有一个私钥。

预备知识

想要彻底了解这个协议，我们需要一些预备知识（如果你没有看懂上面的协议简介的话）。

1.公钥加密机制

在之前HIBE的文章里有涉及到，在公钥密码体中，每个通信方均拥有一个密钥对，即公钥（public key）和私钥（private key），在加密方案中分别用于加密和解密消息，与传统的非对称加密体制不同的是，公钥和私钥是不同的。

2.椭圆曲线算法

椭圆曲线并不是椭圆，而是形如以下形状的关于x轴对称的曲线：

因为涉及群，域等数学概念，我尽量描述得通俗易懂些（可能并不是特别准确，感兴趣的读者可以参考相关资料）。

假设现在随机生成一个秘密密数字a，我们可以把这个数字当作成私钥，然后把它映射到椭圆曲线群上的一个点 a*G，简写为 aG。这个点我们把它当做公钥。

于是我们有：

• sk = a

• PK = aG

椭圆曲线群和有限域之间存在着一种同态双射关系。什么叫双射呢？就是把一个集合X的每个元素都对应集合Y的一个元素，就像下面这样：

有限域，我们用 q这个符号表示，当q为素数的时候，我们管它叫素数域，它是指从 0, 1, 2, …, q-1这样一个整数集合。而在一条椭圆曲线上，我们通过一个基点，G，(确切的说是生成元)可以产生一个循环群，标记为 0G, G, 2G, …, (q-1)G，正好是数量为 q个曲线点的集合。

任意两个曲线点正好可以进行一种类似于加法的二元运算 ，P （假设为2G）+ Q （假设为3G）= R（就是5G），（如上图所示，找到两个相加的点的延长线与椭圆曲线的交点，就得到新的点R）并且满足交换律和结合律。于是我们就用 +这个符号来表示。我们在素数域的加法都可以在椭圆曲线上进行类比，但是椭圆曲线上好像有无穷多个点，我们需要在把椭圆曲线限制到一个有限域内，而我们之所以把这个群称为循环群，因为把群的最后一个元素 (q-1)G，再加上一个 G就回到群的第一个元素 0G。

下面是曲线 

和

的图像。可以发现，椭圆曲线变成了离散的点，且关于y=p/2对称。

给任意一个有限域上的整数 r，我们就可以在循环群中找到一个对应的点 rG，但是反过来给你rG让去找到r是一件很困难的，在密码学中被称为离散对数难题。

也就是说，如果任意给一个椭圆曲线循环群上的点 R，那么到底是有限域中的哪一个整数对应 R，这个计算是很难的，如果有限域足够大，比如说 256bit 这么大，我们姑且可以认为这个反向计算是不可能做到的。

Schnorr 协议充分利用了有限域和循环群之间单向映射，实现了最简单的零知识证明安全协议：证明者向验证者证明她拥有 PK 对应的私钥 sk。

交互式Schnorr协议流程

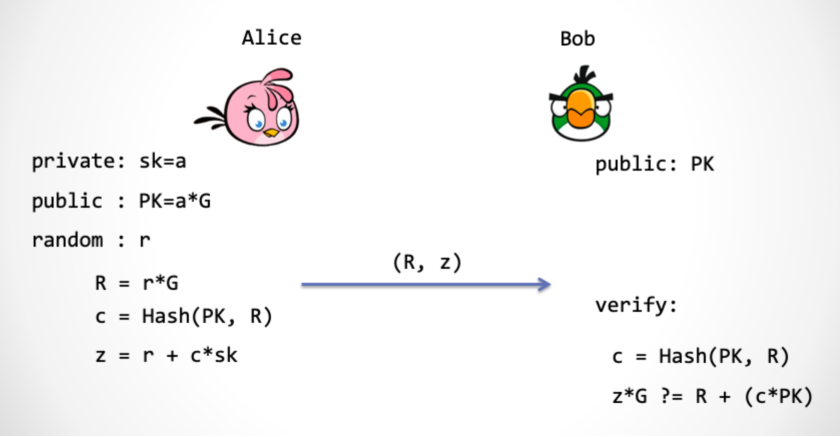
我们让Alice充当证明者，Bob充当验证者，协议流程如下：

Alice：随机地选择一个标量，然后计算出（为椭圆的生成元），将发送给Bob；

Bob：回应一个随机标量；

Alice：通过计算，将标量回应给Bob；

Bob：将z转换为椭圆曲线上的点，即，然后验证

交互过程如下图：

首先我们来复习一下之前所说的零知识证明的三个特性：

（1）完备性。如果证明方和验证方都是诚实的，并遵循证明过程的每一步，进行正确的计算，那么这个证明一定是成功的，验证方一定能够接受证明方。

（2）合理性。没有人能够假冒证明方，使这个证明成功。

（3）零知识性。证明过程执行完之后，验证方只获得了“证明方拥有这个知识”这条信息，而没有获得关于这个知识本身的任何一点信息。

下面我们来一一进行比对：

1.完备性：在等式  等式边同时乘以，便得到，所以说，按照协议里的交互流程，一定能够通过验证者的验证，即验证了完备性。

2.合理性：如果Alice事先不知道私钥的话，那么他是否可以构造出  和  那么是否可以在最后一步验证成功呢？将 带入最后一个需要Bob等式 ，可得，我们在等式两边同时约去  ,可得  ，这其实就是Bob在椭圆曲线上同态地检查 。因为Alice不知道的值，所以就无法得知等式右边的值，自然也就无法找到对应的  和  了。（这里只是一个简单的阐述，更深层的需要了解抽取器的涵义）

3.零知识性：Bob 验证是在椭圆曲线群上完成。Bob知道 映射到曲线上的点，但是不知道本身；Bob 知道  映射到曲线群上的点 ，即，但是不知道  本身。Bob 可以校验  的计算过程是否正确，但是又没有暴露  和  的值（这里只是一个简单的阐述，更深层的需要了解模拟器的含义）。

非交互式Schnorr协议流程

交互式Schnorr 协议中，Bob 需要给出一个随机的挑战数 c，这里我们可以让 Alice 用下面这个式子来计算这个挑战数，  ，因为哈希函数的单向性，虽然 c 是 Alice 计算的，但是 Alice 并没有能力实现通过挑选 c 来作弊。

这样，就把三步Schnorr协议合并为一步。Alice可直接发送（R，z），因为Bob拥有Alice的公钥PK，于是Bob可自行计算出c。然后验证。

这里运用到了Fiat-Shamir协议 ，它可以把整个协议压缩成一步交互，有兴趣的读者可以深入了解相关内容。

结语

在这篇文章中，我们简单地介绍了一个专职零知识证明，schnorr协议。我们又离通用的零知识证明协议更近了一步。下一篇文章我们将会来一起探讨那个深奥的zk-snark，不过在这之前，我们还需要一些预备知识来进行铺垫。

参考：

公众号“安比实验室”：https://github.com/sec-bit/learning-zkp/blob/master/zkp-intro/2/zkp-simu.md

更多相关知识内容：

零知识证明系列之一——初探零知识证明

电子投票系统与区块链

Tips

更多长安链开源项目QA，可登录开源社区、技术文档库查看。

下载源码

https://git.chainmaker.org.cn/chainmaker/chainmaker-go

查阅文档

https://docs.chainmaker.org.cn/

 “长安链ChainMaker”是国内首个自主可控区块链软硬件技术体系，由微芯研究院联合头部企业和高校共同研发，具有全自主、高性能、强隐私、广协作的突出特点。长安链面向大规模节点组网、高交易处理性能、强数据安全隐私等下一代区块链技术需求，融合区块链专用加速芯片硬件和可装配底层软件平台，为构建高性能、高可信、高安全的数字基础设施提供新的解决方案，为长安链生态联盟提供强有力的区块链技术支撑。取名“长安链”，喻意“长治久安、再创辉煌、链接世界”