一、基本知识
1.1 概述
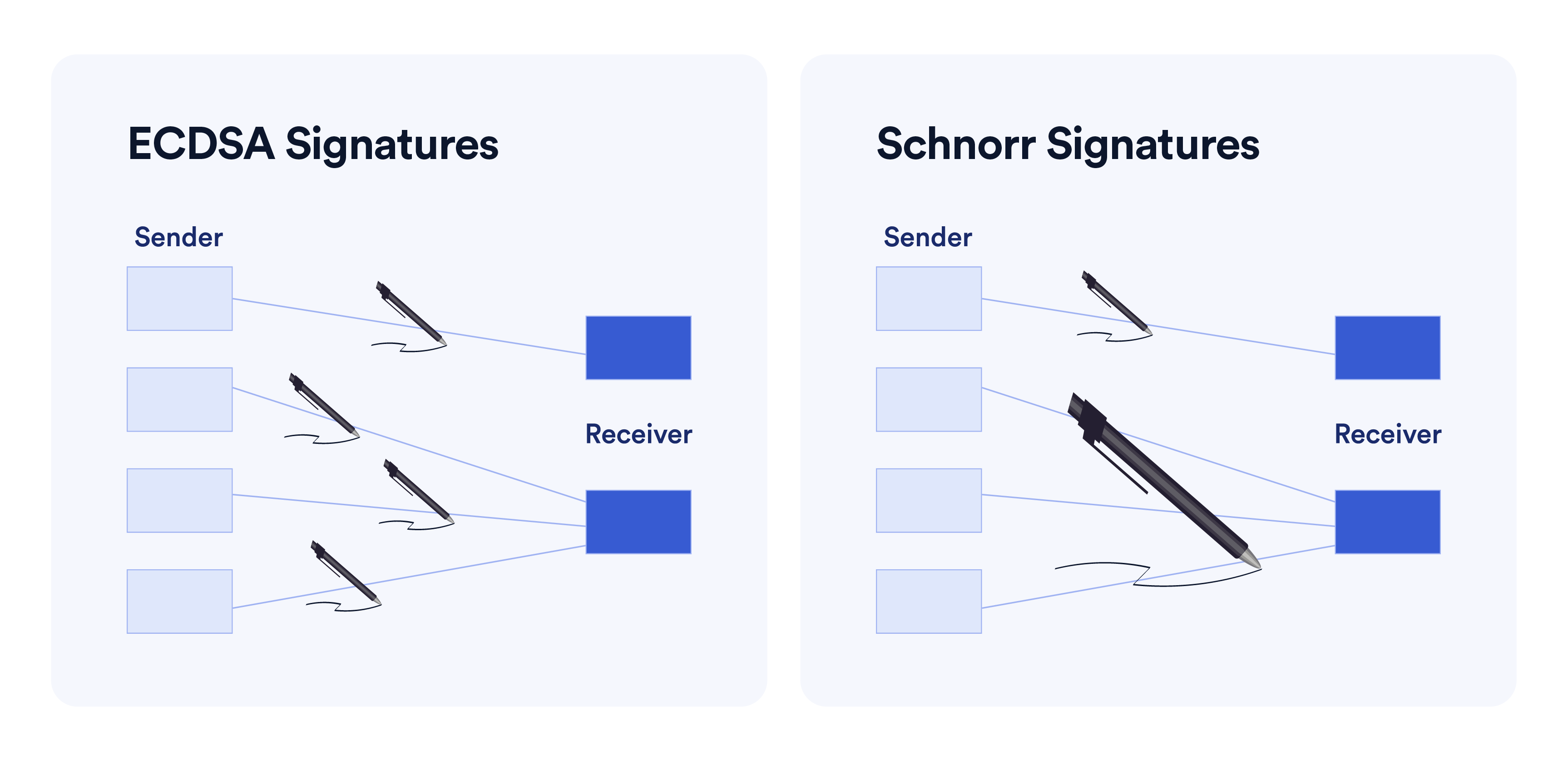
Schnorr签名算法最初是由德国密码学家ClausSchnorr于2008年提出的,在密码学中,它是一种数字签名方案,以其简单高效著称,其安全性基于某些离散对数问题的难处理性。
1.2 椭圆曲线上的计算
密码学中,常用以下形式的椭圆曲线: E : y 2 = x 3 + a x + b ( m o d p ) E: y^2= x^3+ax+b(mod\ p) E:y2=x3+ax+b(mod p) 同时要求 4 a 3 + 27 b 2 ≠ 0 4a^3+27b^2 ≠0 4a3+27b2=0。其中p为一个大素数,a、b、x和y均在有限域 G F ( p ) GF(p) GF(p)中,即从 { 0 , 1 , ⋅ ⋅ ⋅ , p − 1 } \{0,1,···,p-1\} {0,1,⋅⋅⋅,p−1}中取值。该曲线常用 E p ( a , b ) E_{p}(a,b) Ep(a,b)表示。若该曲线上只有有限个离散点,设为N个,则椭圆曲线的阶为N。N越大,椭圆曲线安全性越高。椭圆曲线的阶可通过schoof算法计算求得。
椭圆曲线 E : y 2 = x 3 − x + 1 E: y^2= x^3-x +1 E:y2=x3−x+1图形如下:

加法规则
椭圆曲线 E p ( a , b ) E_{p}(a,b) Ep(a,b)在如下定义的加法规则构成Abel群(交换群)。
- O + O = O Ο + Ο = Ο O+O=O
- ∀ P = ( x , y ) ∈ E p ( a , b ) ∀P=(x,y)∈E_{p}(a,b) ∀P=(x,y)∈Ep(a,b),有 P + O = O + P = P P +Ο =Ο + P = P P+O=O+P=P
- ∀ P = ( x , y ) ∈ E p ( a , b ) ∀P=(x,y)∈E_{p}(a,b) ∀P=(x,y)∈Ep(a,b),有 P + ( − P ) = O P + (-P) =Ο P+(−P)=O, P P P的逆为 − P = ( x , − y ) -P = (x,-y) −P=(x,−y)
- ∀ P = ( x 1 , y 1 ) , Q = ( x 2 , y 2 ) ∈ E p ( a , b ) ∀P=(x_{1},y_{1}),Q=(x_{2},y_{2})∈E_{p}(a,b) ∀P=(x1,y1),Q=(x2,y2)∈Ep(a,b),则 P + Q = R = ( x 3 , y 3 ) ∈ E p ( a , b ) P + Q = R = (x_{3},y_{3})∈E_{p}(a,b) P+Q=R=(x3,y3)∈Ep(a,b),其中 x 3 = λ 2 − x 1 − x 2 , y 3 = λ ( x 1 − x 3 ) − y 1 x_3=λ^2-x_1-x_2 ,y_3=λ(x_1-x_3 )-y_1 x3=λ2−x1−x2,y3=λ(x1−x3)−y1。
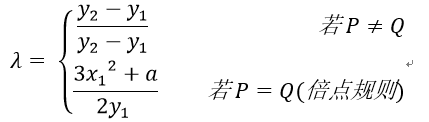
- 相同点相加计算R点

- 不同点相加计算R点

- 不同点相加计算R点
乘法规则
- ∀ k ∈ Z , ∀ P ∈ E p ( a , b ) ∀k∈Z,∀P∈E_p (a,b) ∀k∈Z,∀P∈Ep(a,b),有 k P = P + ⋅ ⋅ ⋅ + P ( k 个 P 相加 ) kP=P+···+P(k个P相加) kP=P+⋅⋅⋅+P(k个P相加);
- ∀ s , t ∈ Z , ∀ P ∈ E p ( a , b ) ∀s,t∈Z, ∀P∈E_p (a,b) ∀s,t∈Z,∀P∈Ep(a,b),有 ( s + t ) P = s P + t P , s ( t P ) = ( s t ) P (s+t)P=sP+tP,s(tP)=(st)P (s+t)P=sP+tP,s(tP)=(st)P
除了无限远的点 O Ο O外,椭圆曲线 E E E任何可以生成所有点的点都可视为 E E E的生成元,但并非 E E E上所有点都可为生成元。
如何选取生成元
- 首先分解椭圆曲线阶 n = r × p n = r × p n=r×p,p需要足够大。
- 令 k = n / p k= n/p k=n/p,随机选取 X ∈ E p ( a , b ) X∈E_p (a,b) X∈Ep(a,b),计算 G = k ⋅ X G = k ·X G=k⋅X
- 若 G ≠ O G ≠ Ο G=O,则 G G G可为生成元否则重新选择 X X X再次计算。
二、算法细节
2.1 公私钥产生算法( K e y G e n KeyGen KeyGen):
- 选择一条椭圆曲线 E p ( a , b ) E_{p}(a,b) Ep(a,b) 和基点 G G G;
- 选择私钥 d A d_{A} dA( d A < n d_{A}<n dA<n, n n n为该 G G G的阶),利用基点 G G G计算公钥 Q A = d A ⋅ G Q_{A}=d_{A} · G QA=dA⋅G;
2.2 签名生成算法( S i g n Sign Sign)
- 选择一个随机整数 k ( k < n ) k(k<n) k(k<n);
- 计算点 R = k ⋅ G = ( x 1 , y 1 ) R=k·G=(x_{1},y_{1}) R=k⋅G=(x1,y1);
- 计算 σ = k + h a s h ( m ∣ ∣ R ) ⋅ d A ( m o d n ) \sigma=k + hash(m|| R)·d_{A} (mod \ n) σ=k+hash(m∣∣R)⋅dA(mod n);
- 得到签名 s = ( R , σ ) s=(R,\sigma) s=(R,σ);
2.3 签名验证算法(Verify):
- 验证等式: σ ⋅ G ≡ h a s h ( m ∣ ∣ R ) ⋅ Q A + R \sigma · G ≡{hash(m|| R)}·Q_{A} + R σ⋅G≡hash(m∣∣R)⋅QA+R;
- 如果等式成立输出1,否则输出0。
Schnorr签名除了上面一种形式外,还有另外一种形式。
2.4 签名生成算法( S i g n Sign Sign)
- 选择一个随机整数 k ( k < n ) k(k<n) k(k<n);
- 计算点 R = k ⋅ G = ( x 1 , y 1 ) R=k·G=(x_{1},y_{1}) R=k⋅G=(x1,y1);
- 计算 α = h a s h ( m ∣ ∣ R ) \alpha=hash(m|| R) α=hash(m∣∣R)
- 计算 σ = k + h a s h ( m ∣ ∣ R ) ⋅ d A ( m o d n ) \sigma=k + hash(m|| R)·d_{A} (mod \ n) σ=k+hash(m∣∣R)⋅dA(mod n);
- 得到签名 s = ( α , σ ) s=(\alpha,\sigma) s=(α,σ);
2.5 签名验证算法(Verify):
- 计算 R ′ = σ ⋅ G − α ⋅ Q A R^{'}=\sigma·G-\alpha·Q_{A} R′=σ⋅G−α⋅QA
- 验证等式: h a s h ( m ∣ ∣ R ′ ) ≡ α hash(m|| R^{'}) ≡\alpha hash(m∣∣R′)≡α;
- 如果等式成立输出1,否则输出0。