1
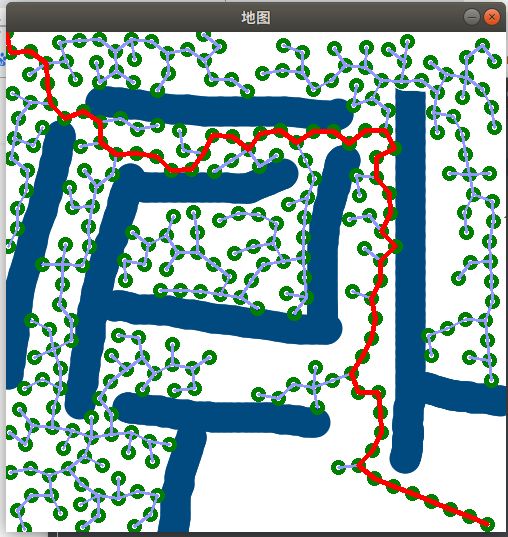
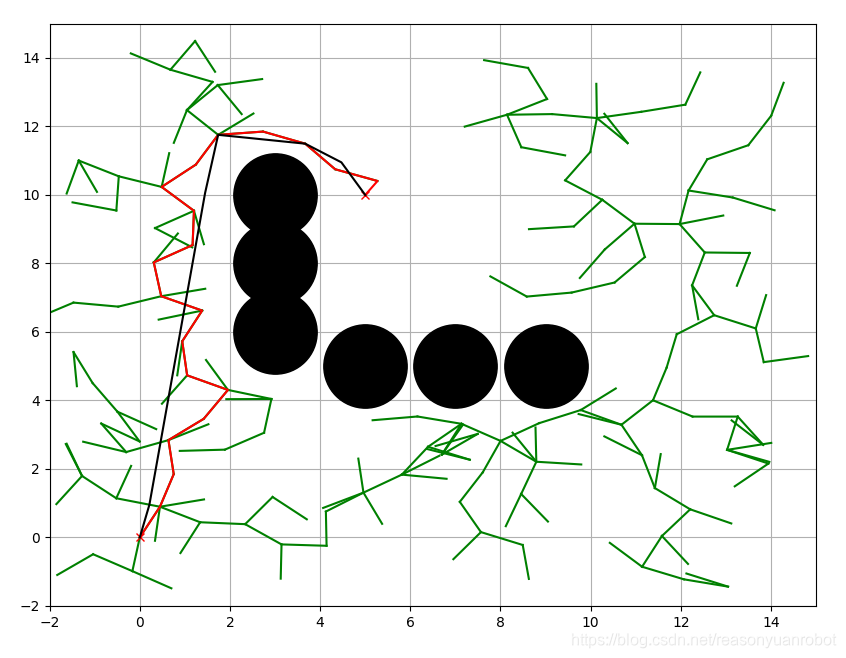
原始RRT算法运行结果:python,这里以2D_rrt及其衍生相关算法为例(边做边更新)
CV搬运工们,先上github连接:(点个赞呗)(不想要拿github包的后面有现成代码)GitHub - zhm-real/PathPlanning: Common used path planning algorithms with animations.
路径算法的讲解可以看路径规划算法_qq_935160072的博客-CSDN博客这篇上放置的B站上up主课程链接
别忘了先阅读README.md,对内容进行简单了解。包含的路径规划算法如下图所示:
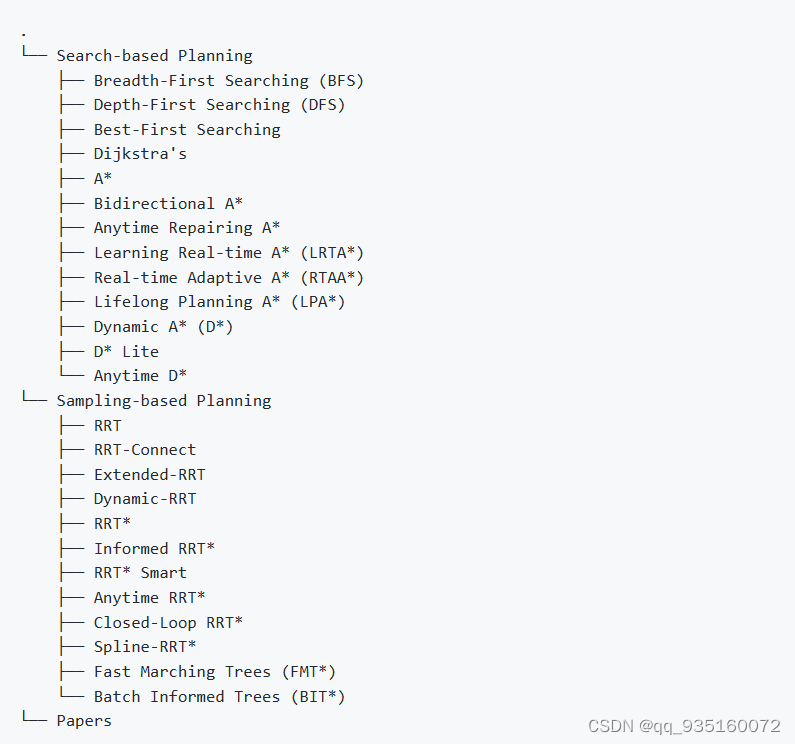
那路径规划有什么用呢阿米特的 A* 页面 (stanford.edu)
直接open整个文件包就OK了
在下载文件包后有报错需要修改:
如果发生 from Sampling_based_Planning.rrt_2D import env, plotting, utils
ModuleNotFoundError: No module named 'Sampling_based_Planning'类似的报错。
from Sampling_based_Planning.rrt_2D import env, plotting, utils将该部分from import 改为
import env
import plotting
import utils如果NO module env,plotting....将对应的代码.py文件该env.py放入rrt.py文件相同的文件夹下即可
该代码是在实现路径规划后再进行绘图显示(需要等待几秒)
!!!!!!!!!!!!!!!!!!!!!!!!!!
必须包含3个.py文件 env,plotting,utils分别包含(障碍物,绘图,碰撞检测)
同样我也贴出来:
env.py:
class Env:def __init__(self):self.x_range = (0, 50)self.y_range = (0, 30)self.obs_boundary = self.obs_boundary()self.obs_circle = self.obs_circle()self.obs_rectangle = self.obs_rectangle()@staticmethoddef obs_boundary():obs_boundary = [[0, 0, 1, 30],[0, 30, 50, 1],[1, 0, 50, 1],[50, 1, 1, 30]]return obs_boundary@staticmethoddef obs_rectangle():obs_rectangle = [[14, 12, 8, 2],[18, 22, 8, 3],[26, 7, 2, 12],[32, 14, 10, 2]]return obs_rectangle@staticmethoddef obs_circle():obs_cir = [[7, 12, 3],[46, 20, 2],[15, 5, 2],[37, 7, 3],[37, 23, 3],#[20, 8, 3],#[31, 20, 3]]return obs_cir
plotting:
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import os
import syssys.path.append(os.path.dirname(os.path.abspath(__file__)) +"/../../Sampling_based_Planning/")import envclass Plotting:def __init__(self, x_start, x_goal):self.xI, self.xG = x_start, x_goalself.env = env.Env()self.obs_bound = self.env.obs_boundaryself.obs_circle = self.env.obs_circleself.obs_rectangle = self.env.obs_rectangledef animation(self, nodelist, path, name, animation=False):self.plot_grid(name)self.plot_visited(nodelist, animation)self.plot_path(path)def animation_connect(self, V1, V2, path, name):self.plot_grid(name)self.plot_visited_connect(V1, V2)self.plot_path(path)def plot_grid(self, name):fig, ax = plt.subplots()for (ox, oy, w, h) in self.obs_bound:ax.add_patch(patches.Rectangle((ox, oy), w, h,edgecolor='black',facecolor='black',fill=True))for (ox, oy, w, h) in self.obs_rectangle:ax.add_patch(patches.Rectangle((ox, oy), w, h,edgecolor='black',facecolor='gray',fill=True))for (ox, oy, r) in self.obs_circle:ax.add_patch(patches.Circle((ox, oy), r,edgecolor='black',facecolor='gray',fill=True))plt.plot(self.xI[0], self.xI[1], "bs", linewidth=3)plt.plot(self.xG[0], self.xG[1], "gs", linewidth=3)plt.title(name)plt.axis("equal")@staticmethoddef plot_visited(nodelist, animation):if animation:count = 0for node in nodelist:count += 1if node.parent:plt.plot([node.parent.x, node.x], [node.parent.y, node.y], "-g")plt.gcf().canvas.mpl_connect('key_release_event',lambda event:[exit(0) if event.key == 'escape' else None])if count % 10 == 0:plt.pause(0.001)else:for node in nodelist:if node.parent:plt.plot([node.parent.x, node.x], [node.parent.y, node.y], "-g")@staticmethoddef plot_visited_connect(V1, V2):len1, len2 = len(V1), len(V2)for k in range(max(len1, len2)):if k < len1:if V1[k].parent:plt.plot([V1[k].x, V1[k].parent.x], [V1[k].y, V1[k].parent.y], "-g")if k < len2:if V2[k].parent:plt.plot([V2[k].x, V2[k].parent.x], [V2[k].y, V2[k].parent.y], "-g")plt.gcf().canvas.mpl_connect('key_release_event',lambda event: [exit(0) if event.key == 'escape' else None])if k % 2 == 0:plt.pause(0.001)plt.pause(0.01)@staticmethoddef plot_path(path):if len(path) != 0:plt.plot([x[0] for x in path], [x[1] for x in path], '-r', linewidth=2)plt.pause(0.01)plt.show()
utils.py:
import math
import numpy as np
import os
import syssys.path.append(os.path.dirname(os.path.abspath(__file__)) +"/../../Sampling_based_Planning/")import envclass Node:def __init__(self, n):self.x = n[0]self.y = n[1]self.parent = Noneclass Utils:def __init__(self):self.env = env.Env() #初始化环境信息self.delta = 0.5self.obs_circle = self.env.obs_circleself.obs_rectangle = self.env.obs_rectangleself.obs_boundary = self.env.obs_boundarydef update_obs(self, obs_cir, obs_bound, obs_rec): #更新环境信息self.obs_circle = obs_cirself.obs_boundary = obs_boundself.obs_rectangle = obs_recdef get_obs_vertex(self): #获取障碍物点delta = self.deltaobs_list = [] #障碍物列表for (ox, oy, w, h) in self.obs_rectangle:vertex_list = [[ox - delta, oy - delta],[ox + w + delta, oy - delta],[ox + w + delta, oy + h + delta],[ox - delta, oy + h + delta]]obs_list.append(vertex_list)return obs_listdef is_intersect_rec(self, start, end, o, d, a, b):v1 = [o[0] - a[0], o[1] - a[1]] #v1=o和a的xy坐标差v2 = [b[0] - a[0], b[1] - a[1]] #v2=b和a的xy坐标差v3 = [-d[1], d[0]]div = np.dot(v2, v3) #v2, v3点乘if div == 0: #点乘等于0表示向量垂直return Falset1 = np.linalg.norm(np.cross(v2, v1)) / divt2 = np.dot(v1, v3) / divif t1 >= 0 and 0 <= t2 <= 1:shot = Node((o[0] + t1 * d[0], o[1] + t1 * d[1]))dist_obs = self.get_dist(start, shot)dist_seg = self.get_dist(start, end)if dist_obs <= dist_seg:return Truereturn Falsedef is_intersect_circle(self, o, d, a, r):d2 = np.dot(d, d)delta = self.deltaif d2 == 0:return Falset = np.dot([a[0] - o[0], a[1] - o[1]], d) / d2if 0 <= t <= 1:shot = Node((o[0] + t * d[0], o[1] + t * d[1]))if self.get_dist(shot, Node(a)) <= r + delta:return Truereturn Falsedef is_collision(self, start, end):if self.is_inside_obs(start) or self.is_inside_obs(end):return Trueo, d = self.get_ray(start, end) #o, d为起点和终点obs_vertex = self.get_obs_vertex() #获取更新的障碍物for (v1, v2, v3, v4) in obs_vertex: #if self.is_intersect_rec(start, end, o, d, v1, v2):return Trueif self.is_intersect_rec(start, end, o, d, v2, v3):return Trueif self.is_intersect_rec(start, end, o, d, v3, v4):return Trueif self.is_intersect_rec(start, end, o, d, v4, v1):return Truefor (x, y, r) in self.obs_circle:if self.is_intersect_circle(o, d, [x, y], r):return Truereturn False#通过改变避障方式,增加判断当发生碰撞时改变扩展方向进行障碍物的避绕def is_inside_obs(self, node): #在障碍物中的数据信息,delta = self.deltafor (x, y, r) in self.obs_circle: #圆形障碍物if math.hypot(node.x - x, node.y - y) <= r + delta:return Truefor (x, y, w, h) in self.obs_rectangle: #矩形障碍物if 0 <= node.x - (x - delta) <= w + 2 * delta \and 0 <= node.y - (y - delta) <= h + 2 * delta:return Truefor (x, y, w, h) in self.obs_boundary: #边界障碍物if 0 <= node.x - (x - delta) <= w + 2 * delta \and 0 <= node.y - (y - delta) <= h + 2 * delta:return Truereturn False@staticmethoddef get_ray(start, end):orig = [start.x, start.y]direc = [end.x - start.x, end.y - start.y] #终点-起始点得到生长方向return orig, direc@staticmethoddef get_dist(start, end):return math.hypot(end.x - start.x, end.y - start.y) #两点间的距离
RRT代码介绍连接:(14条消息) RRT算法简介_魂淡1994的博客-CSDN博客
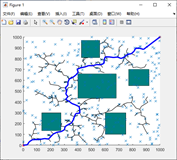
仿真结果如下:
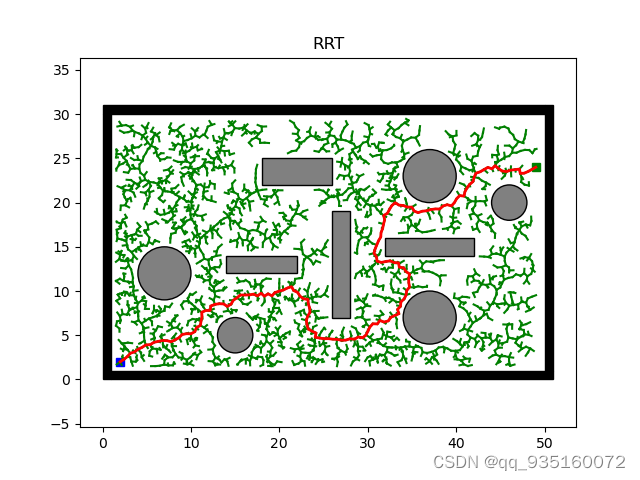
具体代码已经贴出:注释自己写的可能有小错误,可以帮忙指出
import os
import sys
import math
import time
import random
import numpy as npsys.path.append(os.path.dirname(os.path.abspath(__file__)) +"/../../Sampling_based_Planning/")import env #障碍物图
import plotting #画图
import utilsclass Node:def __init__(self, n):self.x = n[0]self.y = n[1]self.parent = Noneclass Rrt:def __init__(self, s_start, s_goal, step_len, goal_sample_rate, iter_max):self.s_start = Node(s_start)self.s_goal = Node(s_goal)self.step_len = step_lenself.goal_sample_rate = goal_sample_rateself.iter_max = iter_maxself.vertex = [self.s_start]self.env = env.Env()self.plotting = plotting.Plotting(s_start, s_goal)self.utils = utils.Utils()self.x_range = self.env.x_rangeself.y_range = self.env.y_rangeself.obs_circle = self.env.obs_circleself.obs_rectangle = self.env.obs_rectangleself.obs_boundary = self.env.obs_boundaryself.iterations = 0def planning(self):for i in range(self.iter_max):node_rand = self.generate_random_node(self.goal_sample_rate) #随机生成的节点node_near = self.nearest_neighbor(self.vertex, node_rand) #最近的节点node_new = self.new_state(node_near, node_rand) #新节点"""######################节点重选择部分node_vector = npv_1 = (node_new[0]-node_near[0], node_new[1]-node_near[1])v_2 = ()######################节点重选择部分"""self.iterations += 1time.sleep(0.001)if node_new and not self.utils.is_collision(node_near, node_new):self.vertex.append(node_new)dist, _ = self.get_distance_and_angle(node_new, self.s_goal)if dist <= self.step_len and not self.utils.is_collision(node_new, self.s_goal):self.new_state(node_new, self.s_goal)return self.extract_path(node_new)return Nonedef generate_random_node(self, goal_sample_rate):delta = self.utils.deltaif random.randint(0, 100) > goal_sample_rate:return Node((np.random.uniform(self.x_range[0] + delta, self.x_range[1] - delta),np.random.uniform(self.y_range[0] + delta, self.y_range[1] - delta)))return self.s_goal@staticmethoddef nearest_neighbor(node_list, n):return node_list[int(np.argmin([math.hypot(nd.x - n.x, nd.y - n.y)for nd in node_list]))]def new_state(self, node_start, node_end):dist, theta = self.get_distance_and_angle(node_start, node_end)dist = min(self.step_len, dist)node_new = Node((node_start.x + dist * math.cos(theta),node_start.y + dist * math.sin(theta)))node_new.parent = node_start#a = math.tan(theta) #根据两点计算角度的弧度#k = -1/a #随机向量垂直的方向#print(k)#print(a)return node_newdef extract_path(self, node_end):path = [(self.s_goal.x, self.s_goal.y)]node_now = node_endwhile node_now.parent is not None:node_now = node_now.parentpath.append((node_now.x, node_now.y))return path@staticmethoddef get_distance_and_angle(node_start, node_end):dx = node_end.x - node_start.xdy = node_end.y - node_start.yreturn math.hypot(dx, dy), math.atan2(dy, dx)def main():start_time = time.time() # 规划时间x_start = (2, 2) # Starting nodex_goal = (49, 24) # Goal noderrt = Rrt(x_start, x_goal, 0.5, 0, 10000) #起点,目标点,步长,随机概率,最大迭代次数path = rrt.planning()print((time.time() - start_time))print(f"迭代次数为: {rrt.iterations}")#print(f"Path length: {path_length}")if path:rrt.plotting.animation(rrt.vertex, path, "RRT", True)count = 0for i in path:count += 1print("距离长度为:" + str(count) + "mm") #路径有问题else:print("No Path Found!")if __name__ == '__main__':main()
RRT算法加入目标偏置概率(random()函数,大于设置值取目标点,小于则取随机生成的点)后随机性明显变小(过大过小均不合适),,,修改注释代表的随机概率即可
def main():start_time = time.time() # 规划时间x_start = (2, 2) # Starting nodex_goal = (49, 24) # Goal noderrt = Rrt(x_start, x_goal, 0.5, 0, 10000) #起点,目标点,步长,随机概率,最大迭代次数path = rrt.planning()print((time.time() - start_time))print(f"迭代次数为: {rrt.iterations}")#print(f"Path length: {path_length}")if path:rrt.plotting.animation(rrt.vertex, path, "RRT", True)count = 0for i in path:count += 1print("距离长度为:" + str(count) + "mm") #路径有问题else:print("No Path Found!")if __name__ == '__main__':main()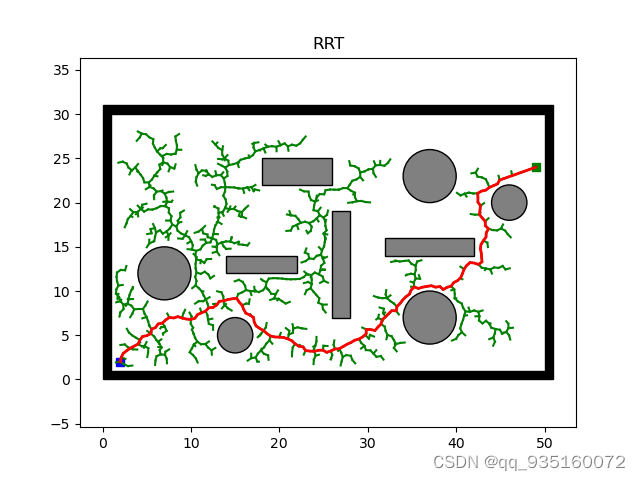
RRT-connect算法采用双向搜索树交替进行搜索(包括目标偏置和贪婪算法)原理介绍链接:(14条消息) RRT-connect算法__yuan_的博客-CSDN博客
代码如下(同样贪婪算法部分也标注出来了):
import os
import sys
import math
import copy
import random
import time
import numpy as np
import matplotlib.pyplot as pltsys.path.append(os.path.dirname(os.path.abspath(__file__)) +"/../../Sampling_based_Planning/")import env
import plotting
import utilsclass Node: #定义一个节点def __init__(self, n):self.x = n[0]self.y = n[1]self.parent = Noneclass RrtConnect:def __init__(self, s_start, s_goal, step_len, goal_sample_rate, iter_max):self.s_start = Node(s_start)self.s_goal = Node(s_goal)self.step_len = step_lenself.goal_sample_rate = goal_sample_rateself.iter_max = iter_maxself.V1 = [self.s_start]self.V2 = [self.s_goal]self.env = env.Env()self.plotting = plotting.Plotting(s_start, s_goal)self.utils = utils.Utils()self.x_range = self.env.x_rangeself.y_range = self.env.y_rangeself.obs_circle = self.env.obs_circle #更新圆形障碍物self.obs_rectangle = self.env.obs_rectangle #更新矩形障碍物self.obs_boundary = self.env.obs_boundary #更新地图边界self.iterations = 0 #初始化迭代次数为0def planning(self): #定义函数获取路径for i in range(self.iter_max):node_rand = self.generate_random_node(self.s_goal, self.goal_sample_rate) #随机点=产生目标点和目标概率node_near = self.nearest_neighbor(self.V1, node_rand) #最近的点与随机点的V1距离node_new = self.new_state(node_near, node_rand) #new_state()函数返回新节点self.iterations += 1 #迭代次数+1time.sleep(0.001)if node_new and not self.utils.is_collision(node_near, node_new): #utils.py文件中进行碰撞检测self.V1.append(node_new) #无碰撞后将新节点加入(V1)中node_near_prim = self.nearest_neighbor(self.V2, node_new) #返回最近节点赋值给node_near_prim(根据最近节点获取方向,得到下面的)node_new_prim = self.new_state(node_near_prim, node_new) #将新生成的节点赋值给node_new_prim"""######################贪婪算法部分if node_new_prim and not self.utils.is_collision(node_new_prim, node_near_prim): #如果新节点也不发生碰撞(新生成的节点,最近的节点)#self.V2.append(node_new_prim) #将新生成的节点加入V2#while True: #发生碰撞则进行下列操作#node_new_prim2 = self.new_state(node_new_prim, node_new) #因为第一棵树碰撞,与第二棵树交换进行#if node_new_prim2 and not self.utils.is_collision(node_new_prim2, node_new_prim): #如果与第二棵树没发生碰撞(第二棵树的节点,新生成的节点)#self.V2.append(node_new_prim2) #然后将该节点加入V2中#node_new_prim = self.change_node(node_new_prim, node_new_prim2) #交换节点后赋值为新节点#else:#break#if self.is_node_same(node_new_prim, node_new):#break#######################贪婪算法部分"""if self.is_node_same(node_new_prim, node_new): #is_node_same函数判断新节点是不是目标点return self.extract_path(node_new, node_new_prim) #返回路径if len(self.V2) < len(self.V1): #对比第一棵树和第二棵树的长度,平衡随机树长度,交换list_mid = self.V2self.V2 = self.V1self.V1 = list_mid"""判断偶数进行树扩展的交换if i % 2 == 0: list_mid = self.V2self.V2 = self.V1self.V1 = list_mid"""return None@staticmethoddef change_node(node_new_prim, node_new_prim2): #交换节点node_new = Node((node_new_prim2.x, node_new_prim2.y)) #将第二课树的节点赋值为新节点node_new.parent = node_new_prim #将node_new_prim赋值给父节点return node_new@staticmethoddef is_node_same(node_new_prim, node_new): #如果新节点是目标点,则返回Trueif node_new_prim.x == node_new.x and \node_new_prim.y == node_new.y:return Truereturn Falsedef generate_random_node(self, sample_goal, goal_sample_rate): #随机生成数大于目标概率则生成随机点,否则去目标点作为随机点delta = self.utils.deltaif random.randint(0, 100) > goal_sample_rate:return Node((np.random.uniform(self.x_range[0] + delta, self.x_range[1] - delta),np.random.uniform(self.y_range[0] + delta, self.y_range[1] - delta)))return sample_goal@staticmethoddef nearest_neighbor(node_list, n): #从节点列表中找到最近节点,并返回return node_list[int(np.argmin([math.hypot(nd.x - n.x, nd.y - n.y) #返回最近的节点for nd in node_list]))]def new_state(self, node_start, node_end): #函数获得新节点扩展的位置dist, theta = self.get_distance_and_angle(node_start, node_end) #获得了距离,角度dist = min(self.step_len, dist)node_new = Node((node_start.x + dist * math.cos(theta),node_start.y + dist * math.sin(theta)))node_new.parent = node_start #将父节点作为起点print(theta) #(theta)<0代表向下,>0代表向下return node_new #返回新节点位置@staticmethoddef extract_path(node_new, node_new_prim): #获得生成的路径(path1 + path2)path1 = [(node_new.x, node_new.y)]node_now = node_newwhile node_now.parent is not None:node_now = node_now.parentpath1.append((node_now.x, node_now.y))path2 = [(node_new_prim.x, node_new_prim.y)]node_now = node_new_primwhile node_now.parent is not None:node_now = node_now.parentpath2.append((node_now.x, node_now.y))return list(list(reversed(path1)) + path2)@staticmethoddef get_distance_and_angle(node_start, node_end): #根据开始的节点和最后的节点获取距离和角度dx = node_end.x - node_start.xdy = node_end.y - node_start.yreturn math.hypot(dx, dy), math.atan2(dy, dx) #hypot()函数计算两点间的距离def main():start_time = time.time() # 规划时间x_start = (2, 2) # 起始节点x_goal = (49, 24) # 最终节点rrt_connect = RrtConnect(x_start, x_goal, 0.5, 0, 5000) #起点,目标点,步长,随机概率,最大迭代次数path = rrt_connect.planning()print((time.time() - start_time))print(f"迭代次数为: {rrt_connect.iterations}")rrt_connect.plotting.animation_connect(rrt_connect.V1, rrt_connect.V2, path, "RRT_CONNECT")if __name__ == '__main__':main()
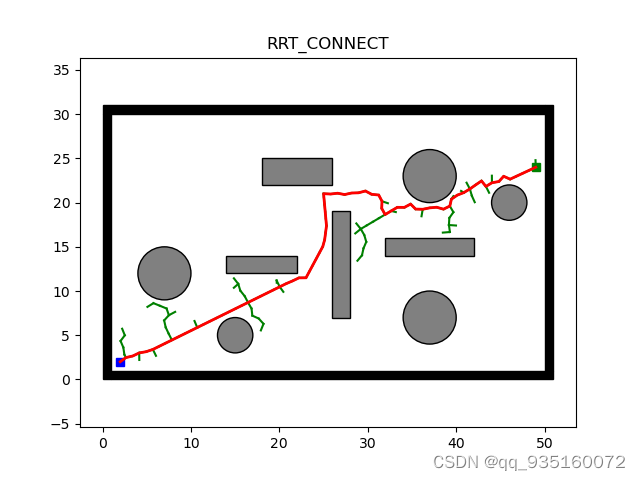
将贪婪算法部分注释掉后的运行结果(为了方便阅读,将全文注释了一遍,但是有些部分目前还没看懂)
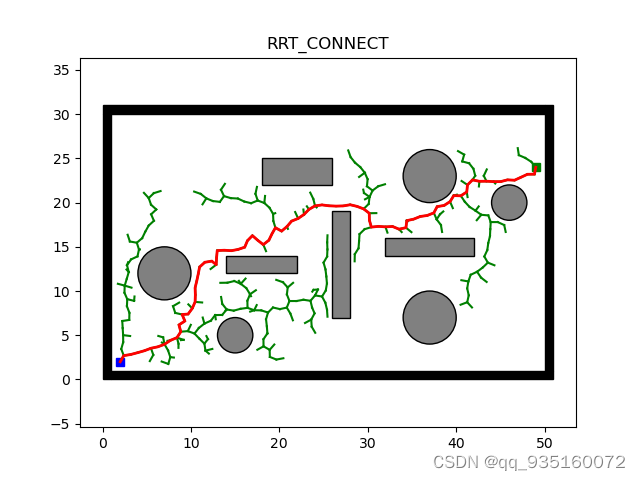
RRT*是渐进优化算法(等待时间较长)
代码如下:
"""
RRT_star 2D
@author: huiming zhou
"""import os
import sys
import math
import time
import numpy as npsys.path.append(os.path.dirname(os.path.abspath(__file__)) +"/../../Sampling_based_Planning/")import env
import plotting
import utils
import queueclass Node:def __init__(self, n):self.x = n[0]self.y = n[1]self.parent = Noneclass RrtStar:def __init__(self, x_start, x_goal, step_len,goal_sample_rate, search_radius, iter_max):self.s_start = Node(x_start)self.s_goal = Node(x_goal)self.step_len = step_lenself.goal_sample_rate = goal_sample_rateself.search_radius = search_radiusself.iter_max = iter_maxself.vertex = [self.s_start]self.path = []self.env = env.Env()self.plotting = plotting.Plotting(x_start, x_goal)self.utils = utils.Utils()self.x_range = self.env.x_rangeself.y_range = self.env.y_rangeself.obs_circle = self.env.obs_circleself.obs_rectangle = self.env.obs_rectangleself.obs_boundary = self.env.obs_boundaryself.iterations = 0def planning(self):for k in range(self.iter_max):node_rand = self.generate_random_node(self.goal_sample_rate)node_near = self.nearest_neighbor(self.vertex, node_rand)node_new = self.new_state(node_near, node_rand)self.iterations += 1time.sleep(0.001)if k % 500 == 0:print(k)if node_new and not self.utils.is_collision(node_near, node_new):neighbor_index = self.find_near_neighbor(node_new)self.vertex.append(node_new)if neighbor_index:self.choose_parent(node_new, neighbor_index)self.rewire(node_new, neighbor_index)index = self.search_goal_parent()self.path = self.extract_path(self.vertex[index])self.plotting.animation(self.vertex, self.path, "rrt*, N = " + str(self.iter_max))def new_state(self, node_start, node_goal):dist, theta = self.get_distance_and_angle(node_start, node_goal)dist = min(self.step_len, dist)node_new = Node((node_start.x + dist * math.cos(theta),node_start.y + dist * math.sin(theta)))node_new.parent = node_startreturn node_newdef choose_parent(self, node_new, neighbor_index):cost = [self.get_new_cost(self.vertex[i], node_new) for i in neighbor_index]cost_min_index = neighbor_index[int(np.argmin(cost))]node_new.parent = self.vertex[cost_min_index]def rewire(self, node_new, neighbor_index):for i in neighbor_index:node_neighbor = self.vertex[i]if self.cost(node_neighbor) > self.get_new_cost(node_new, node_neighbor):node_neighbor.parent = node_newdef search_goal_parent(self):dist_list = [math.hypot(n.x - self.s_goal.x, n.y - self.s_goal.y) for n in self.vertex]node_index = [i for i in range(len(dist_list)) if dist_list[i] <= self.step_len]if len(node_index) > 0:cost_list = [dist_list[i] + self.cost(self.vertex[i]) for i in node_indexif not self.utils.is_collision(self.vertex[i], self.s_goal)]return node_index[int(np.argmin(cost_list))]return len(self.vertex) - 1def get_new_cost(self, node_start, node_end):dist, _ = self.get_distance_and_angle(node_start, node_end)return self.cost(node_start) + distdef generate_random_node(self, goal_sample_rate):delta = self.utils.deltaif np.random.random() > goal_sample_rate:return Node((np.random.uniform(self.x_range[0] + delta, self.x_range[1] - delta),np.random.uniform(self.y_range[0] + delta, self.y_range[1] - delta)))return self.s_goaldef find_near_neighbor(self, node_new):n = len(self.vertex) + 1r = min(self.search_radius * math.sqrt((math.log(n) / n)), self.step_len)dist_table = [math.hypot(nd.x - node_new.x, nd.y - node_new.y) for nd in self.vertex]dist_table_index = [ind for ind in range(len(dist_table)) if dist_table[ind] <= r andnot self.utils.is_collision(node_new, self.vertex[ind])]return dist_table_index@staticmethoddef nearest_neighbor(node_list, n):return node_list[int(np.argmin([math.hypot(nd.x - n.x, nd.y - n.y)for nd in node_list]))]@staticmethoddef cost(node_p):node = node_pcost = 0.0while node.parent:cost += math.hypot(node.x - node.parent.x, node.y - node.parent.y)node = node.parentreturn costdef update_cost(self, parent_node):OPEN = queue.QueueFIFO()OPEN.put(parent_node)while not OPEN.empty():node = OPEN.get()if len(node.child) == 0:continuefor node_c in node.child:node_c.Cost = self.get_new_cost(node, node_c)OPEN.put(node_c)def extract_path(self, node_end):path = [[self.s_goal.x, self.s_goal.y]]node = node_endwhile node.parent is not None:path.append([node.x, node.y])node = node.parentpath.append([node.x, node.y])return path@staticmethoddef get_distance_and_angle(node_start, node_end):dx = node_end.x - node_start.xdy = node_end.y - node_start.yreturn math.hypot(dx, dy), math.atan2(dy, dx)def main():start_time = time.time() # 规划时间x_start = (2, 2) # Starting nodex_goal = (49, 24) # Goal noderrt_star = RrtStar(x_start, x_goal, 1, 0, 20, 10000)rrt_star.planning()print((time.time() - start_time))print(f"迭代次数为: {rrt_star.iterations}")if __name__ == '__main__':main()
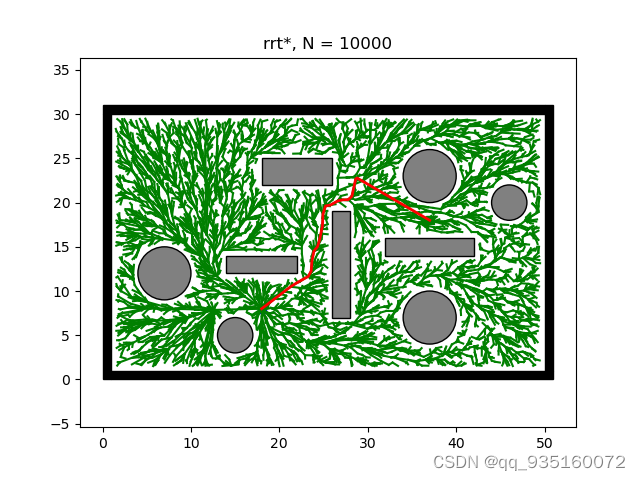
这三种算法的介绍连接如下 :(12条消息) RRT、RRT_Connect、RRT*_-点灯-的博客-CSDN博客_rrt-connect