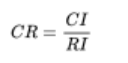权重计算方法一：层次分析法（AHP）

article/2025/9/12 2:34:16

目录

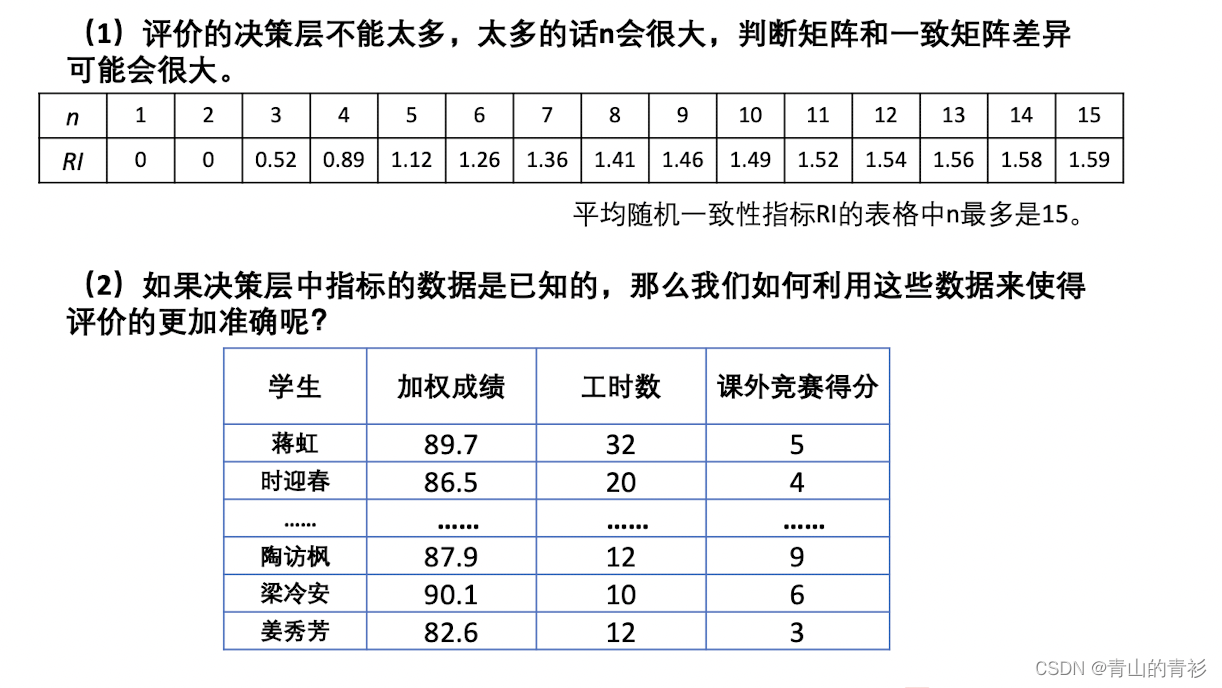
1.层次分析法原理介绍

2.层次分析法建模步骤

3.案例分析

3.1 题目简述

3.2 确定评价指标，建立层次关系

3.3 构造判断矩阵

3.3.1 标度定义

3.3.2 构造判断矩阵

 3.4 一致性检验

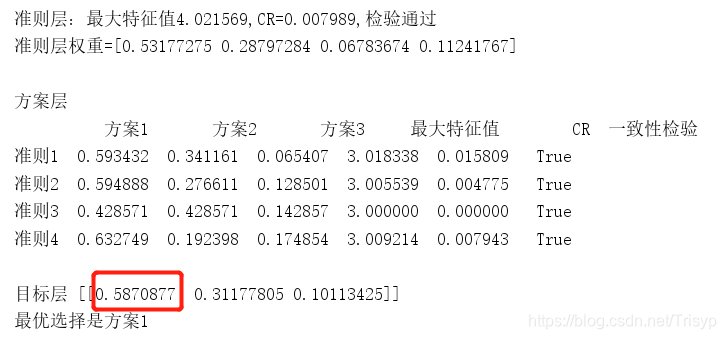
3.5 层次总排序

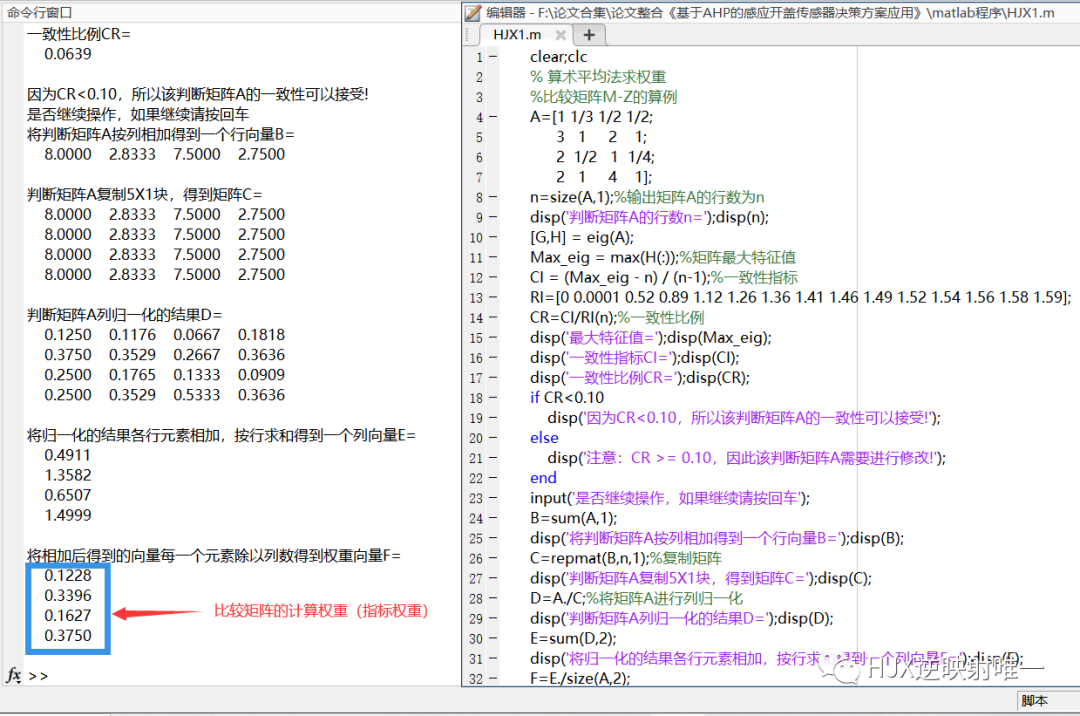
4.代码实现

1.层次分析法原理介绍

        关于层次分析法的具体原理即详细的步骤以及有很多人发布，可自行搜索查看，以下链接为个人认为较好的两篇：数学建模方法——层次分析法（AHP）_Learning-Deep-CSDN博客_层次分析法列向量归一化计算0. 层次分析法简介层次分析法（Analytic Hierarchy Process，简称AHP）主要是对于定性的决策问题进行定量化分析的方法。举个例子，在日常生活中，我们经常需要进行感性的判断，比如报高考志愿，感觉清华北大都很好，到底要报哪个；再比如去市场买菜，到底是买青椒做青椒炒鸡蛋，还是买黄瓜做黄瓜炒鸡蛋；再比如想去出游，到底是去公园A还是公园B。上面提到的这些问题，都是决策，也叫做评价类...https://blog.csdn.net/limiyudianzi/article/details/103389880?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164386596716780261988153%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164386596716780261988153&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-103389880.pc_search_insert_es_download&utm_term=AHP&spm=1018.2226.3001.4187

【AHP】层次分析法 | 过程解读 案例实践_Fxtack的博客-CSDN博客_ahp分析法完整案例AHP 层次分析法一. AHP 层次分析法介绍AHP 层次分析法简介AHP，即层次分析法（Analytic Hierarchy Process,AHP）是一种系统化的、层次化的多目标综合评价方法。在评价对象的待评价属性复杂多样，结构各异，难以量化的情况下AHP层次分析法也能发挥作用。AHP 基本思想 [1]AHP 把复杂的问题分解为各个组成因素，又将这些因素按支配关系分组形成地递阶层次结构。通过两两比较的方式确定方式确定层次中诸因素的相对重要性。然后综合有人员的判断，确定备选方案相对重要https://blog.csdn.net/weixin_43095238/article/details/108055579?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164386596716780261988153%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164386596716780261988153&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-2-108055579.pc_search_insert_es_download&utm_term=AHP&spm=1018.2226.3001.4187

2.层次分析法建模步骤

3.案例分析

3.1 题目简述

        假定现需要购置一批冰箱，由于市场上冰箱种类参差不齐，其性能及性价比也存在很大差异，现有一批冰箱待选择，请考虑冰箱的容积、功耗、外观、噪声、寿命、价格、保修时间等因素，建立模型，确定性价比最高的购买方案。

量化后冰箱参数：

以冰箱A为基准，若该项性能优于A则其值加1，且每优一级都加1，反之亦然。

容积功耗外观噪声寿命价格保修时间
A5555555
B6838797
C24828510

3.2 确定评价指标，建立层次关系

3.3 构造判断矩阵

3.3.1 标度定义

标度含义
1两个要素相比，重要性相同
3两要素相比，前者比后者稍微重要或有优势
5两要素相比，前者比后者比较重要或有优势
7两要素相比，前者比后者十分重要或有优势
9两要素相比，前者比后者绝对重要或有优势
2,4,6,8为上述标度之间的中间值

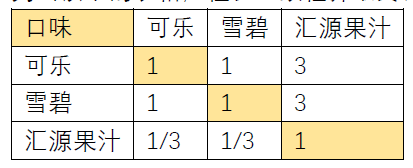
若要描述后者与前者比较，则用倒数为标度。例如 1/3 描述的是，后者比前者稍微重要。 

3.3.2 构造判断矩阵

属性容积功耗外观噪声寿命价格保修时间
容积

1

3

2

1/2

1/3

1/6

1/2

功耗

1/3

1

5

1

1/3

1/2

1/2

外观

1/2

1/5

1

1/3

1/3

1/4

1/3

噪声

2

1

3

1

1/3

1/3

1/3

寿命

3

3

3

3

1

1/2

1/2

价格

6

2

4

3

1

1

3

保修时间

2

2

3

3

2

1/3

1

 3.4 一致性检验

具体的计算方法见推荐阅读的两篇文章。

经过计算得到C.R=0,025<0.1，故一致性检验成功。

 得到七种属性的权值如下：

属性容积功耗外观噪声寿命价格保修时间
权值0.090.100.050.100.180.290.19

3.5 层次总排序

属性容积功耗外观噪声寿命价格保修时间评分
权值0.090.100.050.100.180.290.19
A55555555
B68387977.49
C248285105.97

 由此可见评分：B>C>A。故冰箱B对顾客来说性价比最高。

4.代码实现

package AHP;import java.util.Scanner;public class AHP {public static void main(String[] args) {System.out.println("输入矩阵阶数：");Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();System.out.println("按行输入：");double d[][] = new double[n][n];double temp[][] = new double[n][n];for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) {double sToD = SToD(scanner.next());d[i][j] = sToD;temp[i][j] = sToD;}}System.out.println("以下是判断矩阵");// 得到判断矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.printf("%.2f\t", d[i][j]);}System.out.println();}// 1.对判断矩阵进行求和System.out.println("列相加结果w1");double w1[] = new double[n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {w1[i] = w1[i] + d[j][i];}System.out.printf("%.2f\t", w1[i]);}// 2.相除System.out.println();for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {d[i][j] = d[i][j] / w1[j];}}System.out.println("和积法第一步求出的结果d（即对列向量归一化）：");for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.printf("%.2f\t", d[i][j]);}System.out.println();}System.out.println("对第一步求出的结果进行 行相加");System.out.println("行相加结果w2:");double w2[] = new double[n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {w2[i] = w2[i] + d[i][j];}System.out.printf("\t%.2f\n", w2[i]);}System.out.println("特征向量求解第一步 ： 将上面的行相加的所有结果相加sum：");double sum = 0.0;for (int i = 0; i < n; i++) {sum += w2[i];}System.out.printf("结果为sum = \t%.2f\n", sum);System.out.println("将行结果与 sum 相除 得出结果为w3：  ");double w3[] = new double[n];for (int i = 0; i < n; i++) {w3[i] = w2[i] / sum;System.out.printf("\t%.2f\n", w3[i]);}System.out.println();System.out.println("************************************************");System.out.println("用和积法计算其最大特征向量为（即权重）：W = ");// 以下是校验System.out.printf("(");for (int i = 0; i < n; i++) {System.out.printf("%.2f ,", w3[i]);}System.out.printf(")");System.out.print("\nBW(w4) = ");//BW即行相加结果double w4[] = new double[n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {w4[i] = w4[i] + temp[i][j] * w3[j];}System.out.printf("%.5f \t", w4[i]);}System.out.println("\n----------------------------------------");double sum2 = 0.0;for (int i = 0; i < n; i++) {sum2 = sum2 + w4[i];}System.out.printf("得到最大特征值sum2：\t %.2f\n", sum2);System.out.println("************************************************");System.out.println("最大的特征向量为 ：  ");double result = 0.0;for (int i = 0; i < n; i++) {result = result + w4[i] / (6 * w3[i]);}System.out.printf(" %.2f \n", result);System.out.println("\n判断矩阵一致性指标C.I.(Consistency Index)");double CI = (result - n) / (n - 1);System.out.printf(" %.2f \n", CI);System.out.println("随机一致性比率C.R.(Consistency Ratio)");/** n  1  2  3  	4  		5	  6	  7		  8		 9	  10	  11RI  0  0  0.58  0.90  1.12  1.24  1.36  1.41  1.45  1.49  1.51 一般，当一致性比率 <0.1 时的不一致程度在容许范围之内，可用其归一化特征向量作为权向量，否则要重新构造成对比较矩阵，对  加以调整*/double RI = 0.0;switch (n) {case 0:RI=0;break;case 1:RI=0;break;case 2:RI=0;break;case 3:RI=0.58;break;case 4:RI=0.90;break;case 5:RI=1.12;break;case 6:RI=1.24;break;case 7:RI=1.36;break;default:break;}double CR=CI / RI;if(CR<0.1) {System.out.printf("一致性检验成功！  C.R =  %.2f \n", CR);}elseSystem.out.printf("一致性检验失败！  C.R =  %.2f \n", CR);scanner.close();}public static double SToD(String s) {String[] p = s.split("/");if (p.length > 1) {return Double.parseDouble(p[0]) / Double.parseDouble(p[1]);}return Double.parseDouble(s);}
}


http://chatgpt.dhexx.cn/article/oi33sR7n.shtml

相关文章

【数学建模】层次分析法（AHP）

【数学建模】层次分析法（AHP）

层次分析法 文章目录 层次分析法用途一、模型介绍一道典型例题1.建立层次结构2.对于同一层次的个元素关于上一层次中的某一准则的重要性进行两两比较&#xff0c;构造两两比较矩阵&#xff08;判断矩阵&#xff09;。2.1 O-C矩阵&#xff08;确定指标的权重&#xff09;2.2 准则…
阅读更多...
什么是AHP 层次分析法？

什么是AHP 层次分析法？

AHP层次分析法(The analytic hierarchy process)是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。该方法将定量分析与定性分析结合起来&#xff0c;用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度&#xff0c;并合理地给出每个决策…
阅读更多...
[评价体系] 2、层次分析法AHP原理、例题

[评价体系] 2、层次分析法AHP原理、例题

目录 1 基本介绍 2 建立步骤 2.1 建立递阶式层次结构模型 2.2 构造比较判断矩阵 2.3 层次单排序及一致性检验 2.4 层次总排序及其一致性检验 2.5 数据加权 3 案例&#xff1a;某学科创新能力评价指标体系 3.1 构建评价指标体系 3.2 构造判断矩阵及一致性检验 3.3 …
阅读更多...
数学建模方法——层次分析法（AHP）

数学建模方法——层次分析法（AHP）

目录&#xff1a; 层次分析法简介层次分析法基本原理构造判断矩阵一致性检验一致性检验通过的判断矩阵求权重 4.1 算数平均法求权重 4.2 几何平均法求权重 4.3 特征值法求权重总结 0. 层次分析法简介 层次分析法&#xff08;Analytic Hierarchy Process&#xff0c;简称AHP&…
阅读更多...
层次分析法（AHP）算法简介

层次分析法（AHP）算法简介

一、模型介绍 层次分析法&#xff08;AHP&#xff09;是美国运筹学家萨蒂于上世纪70年代初&#xff0c;为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时&#xff0c;应用网络系统理论和多目标综合评价方法&#xff0c;提出的一种层次权重决策分…
阅读更多...
层次分析法（AHP）原理_例题应用及代码

层次分析法（AHP）原理_例题应用及代码

层次分析法（AHP）原理应用及代码 1.AHP算法步骤2.算法举例第一步：建立递阶层次图第二步：建立判断矩阵计算五个指标的判断矩阵计算三个方案相对于某一指标的权重第三步：进行一致性检验一致性检验的步骤第一步：计算一致性指标 C I CI CI第二步：查找对应的平均随机一致性指标…
阅读更多...
小话层次分析法（AHP）

小话层次分析法（AHP）

在目标决策领域&#xff0c;有的决策数据信息是量化的&#xff0c;如一个项目的未来收益、消耗成本等&#xff0c;通过对各种信息进行计算可以做出较好的决策&#xff1b;但有的决策数据信息并不全是数字化的&#xff0c;如项目信息为“这个收益更好”、“这个成本更高”这样的…
阅读更多...
清风数学建模学习笔记——层次分析法（AHP）

清风数学建模学习笔记——层次分析法（AHP）

层次分析法 层次分析法&#xff08;analytic hierarchy process&#xff09;&#xff0c;简称AHP。是建模比赛中比较基础的模型之一&#xff0c;其主要解决评价类的问题。如选择哪种方案最好&#xff0c;哪位员工表现最好等。 它是一个较为 主观 的评价方法&#xff0c;其在赋权…
阅读更多...
层次分析法-yaahp软件使用

层次分析法-yaahp软件使用

yaahp下载资源&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/1Y08-wgn0YTzrDCaqToZLRg 提取码&#xff1a;avkc 目录 一.打开yaahp软件 1.新建AHP空白文件 2.进入画布页面。 3.点击检查模型按钮&#xff0c;检查模型是否正确 二、构造判断矩阵 1.先创建决策…
阅读更多...
AHP层次分析法详解

AHP层次分析法详解

APH简介 起源 层次分析法&#xff08;AHP&#xff09;是美国运筹学家Saaty于上世纪70年代初&#xff0c;应用网络系统理论和多目标综合评价方法&#xff0c;提出的一种层次权重决策分析方法。层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将…
阅读更多...
AHP（层次分析法）的全面讲解及python实现

AHP（层次分析法）的全面讲解及python实现

一、层次分析法的使用流程&#xff1a; 1. 建立层次结构模型 首先绘出层次结构图&#xff0c;正常三层是比较常见的&#xff1a;决策的目标、考虑的决策准则因素和决策对象。按它们之间的相互关系分为最高层、中间层和最低层&#xff08;如下图是四层结构的&#xff09; 2. 分…
阅读更多...
层次分析法（AHP）基础概念整理+步骤总结

层次分析法（AHP）基础概念整理+步骤总结

层次分析法是用来根据多种准则&#xff0c;或是说因素从候选方案中选出最优的一种数学方法 递阶层次的建立与特点 一般分为三层&#xff0c;最上面为目标层&#xff0c;最下面为方案层&#xff0c;中间是准则层或指标层。 最顶层是我们的目标&#xff0c;比如说选leader&…
阅读更多...
层次分析法（AHP）模型的应用案例

层次分析法（AHP）模型的应用案例

层次分析法&#xff08;AHP&#xff09;模型的特点就是通过搭建递阶的层次结构&#xff0c;把我们生活中的判断事件转化到两两比较层次上面&#xff0c;从而把难于定性的判断来变为可实现数据操作的重要程度方面。在实际情况下&#xff0c;决策者可使用层次分析法&#xff08;A…
阅读更多...
层次分析法（AHP）详细步骤

层次分析法（AHP）详细步骤

1. 算法简介 层次分析法&#xff08;AHP&#xff09;是美国运筹学家萨蒂于上世纪70年代初&#xff0c;为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时&#xff0c;应用网络系统理论和多目标综合评价方法&#xff0c;提出的一种层次权重决策分…
阅读更多...
第一讲 综合评价分析—层次分析法（AHP）

第一讲 综合评价分析—层次分析法（AHP）

写在前面&#xff1a;本文仅用于记录清风数模课程的笔记总结 AHP的主要特点是通过建立递阶层次结构&#xff0c;把人类的判断转化到若干因 素两两之间重要度的比较上&#xff0c;从而把难于量化的定性判断转化为可操作的重 要度的比较上面。在许多情况下&#xff0c;决策者可以…
阅读更多...
层次分析法（AHP法）

层次分析法（AHP法）

目录 一、介绍 二、层次分析法的基本原理 三、层次分析法的主要步骤 四、层次分析法评价过程 1&#xff0c;建立多级阶梯的层次结构 2&#xff0c;求判断矩阵A 3&#xff0c;计算相对权重 1&#xff09;求和法 2&#xff09;求根法 4,结果 5&#xff0c;综合重要度计算 一…
阅读更多...
层次分析法（AHP）详解+完整代码

层次分析法（AHP）详解+完整代码

层次分析法&#xff08;AHP&#xff09; 1.算法简述与原理分析 ​ 层次分析法是一种主观赋值评价方法也是一个多指标综合评价算法&#xff0c;常用于综合评价类模型。层次分析法将与决策有关的元素分解成目标、准则、方案等多个层次&#xff0c;并在此基础上进行定性和定量分…
阅读更多...
层次分析法(AHP)，超详解，进来秒懂！！

层次分析法(AHP)，超详解，进来秒懂！！

层次分析法&#xff0c;简称AHP&#xff0c;是指将与决策总是有关的元素分解成目标、准肌、方案等层次&#xff0c;在此基础之上进行定性和定量分析的决策方法&#xff0c;该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年初提出。 接下来&#xff0c;我会分为四个部分来讲…
阅读更多...
AHP层次分析法

AHP层次分析法

层次分析法&#xff08;Analytic Hierarchy Process&#xff0c;简称 AHP&#xff09;是对一些较为复杂、较为模糊的问题作出决策的简易方法&#xff0c;它特别适用于那些难于完全定量分析的问题。人们在进行社会的、经济的以及科学管理领域问题的系统分析中&#xff0c;面临的…
阅读更多...
数学建模 -- 层次分析法（AHP）

数学建模 -- 层次分析法（AHP）

层次分析法的特点&#xff1a;在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上&#xff0c;利用较少的定量信息使决策的思维过程数学化&#xff0c;从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。是对难于完全定量的复杂系统作出…
阅读更多...
推荐文章

Copyright @ 2022~2023