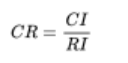层次分析法

用途

评价类问题，如选择哪种方案最好，哪位运动员或者员工表现地更优秀。通常具体数据没有给出。

一、模型介绍

一道典型例题

这是典型的运用层次分析法的题目，没有给出具体数据，要求采取一定措施进行评价，选择最佳方案，其中关键字已经高亮。
我们需要考虑三个问题：
目标、方案、准则。
其中目标和方案一般情况下已知，准则需要我们搜集数据来填写。

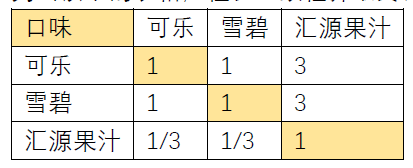
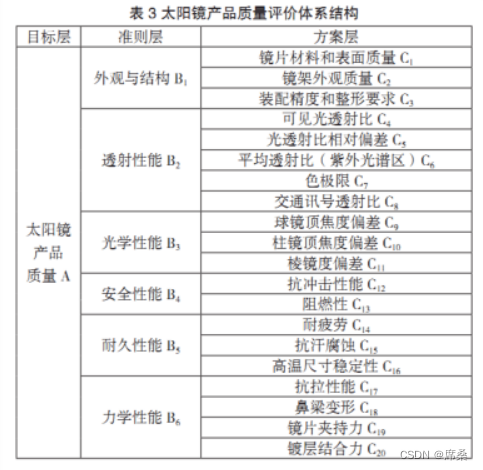
我们的目的是填完如下这张表，加权计算。

1.建立层次结构

这个图需要呈现在论文中

2.对于同一层次的个元素关于上一层次中的某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）。

用于计算权重的矩阵！

下表是用1-9表示重要程度的表

2.1 O-C矩阵（确定指标的权重）

表里是关于 横/竖 满意度的数据

2.2 准则层—方案层的判断矩阵

（1）各个景点在某一因素下所占的权重（如三个景点在景色方面所占的权重（或满意度评分））
（2）层次分析法判断矩阵中的元素只能是1-9和他们的倒数。
（3）这写矩阵中的数据要结合实际填写，充分利用题目里的数据。

3. 由判断矩阵计算被比较元素相对于该准则的相对权重（满意度），一致性检验

在使用判断矩阵求权重之前，必须对其进行一致性检验。
我们够早的矩阵是正互反矩阵，但不一定是一致矩阵。

3.1 一致性检验

原理：用于检验我们构造的判断矩阵和一致矩阵是否有太大差别。

第一步：计算一致性指标CI

最大特征值-方阵阶数 / 方阵阶数-1

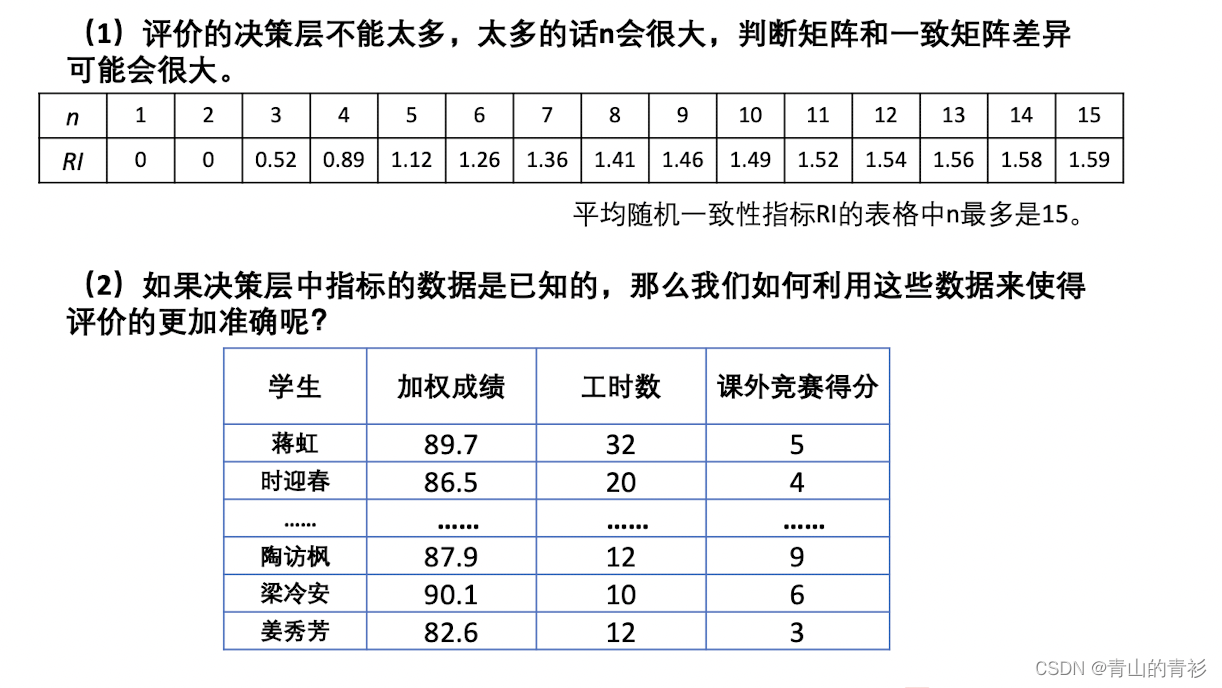
第二步 查找对应的平均一致性指标RI（n<=10)

第三步 计算一致性比例CR

CR>1时，努力向一致矩阵上调整（各行成倍数关系）

3.2 计算权重

一共三种方法，建议全部使用（增强稳健性）

算术平均法

文字表述
公式表述

几何平均法

特征值法

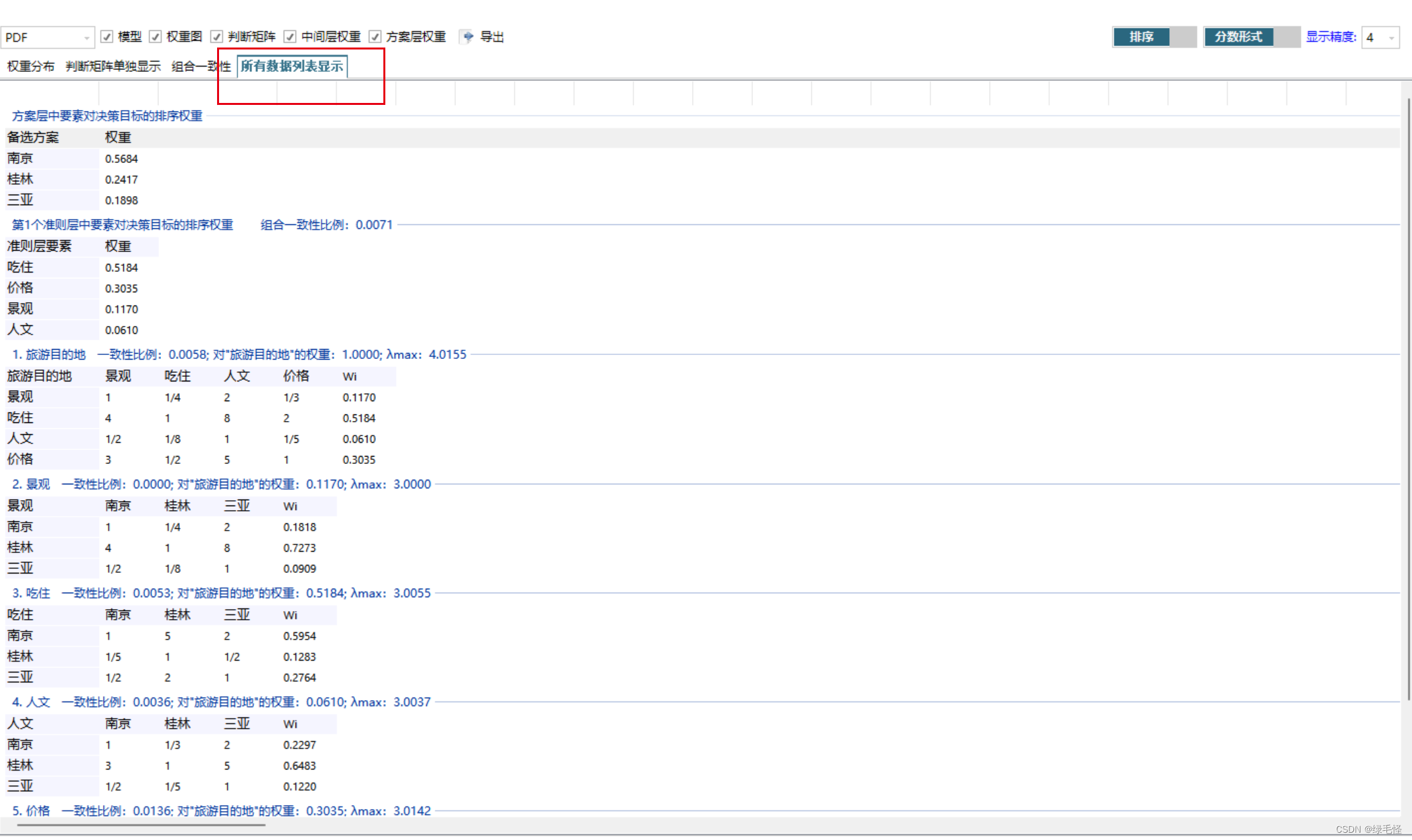
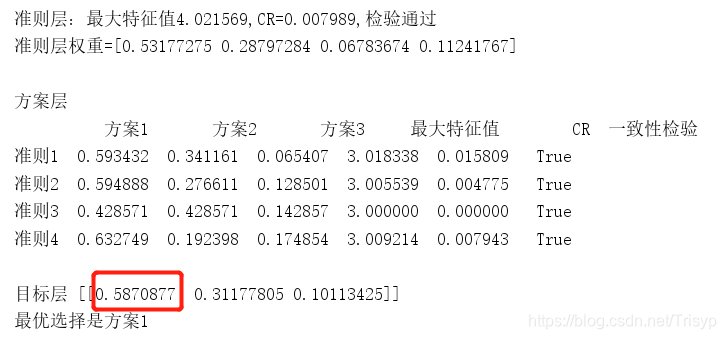
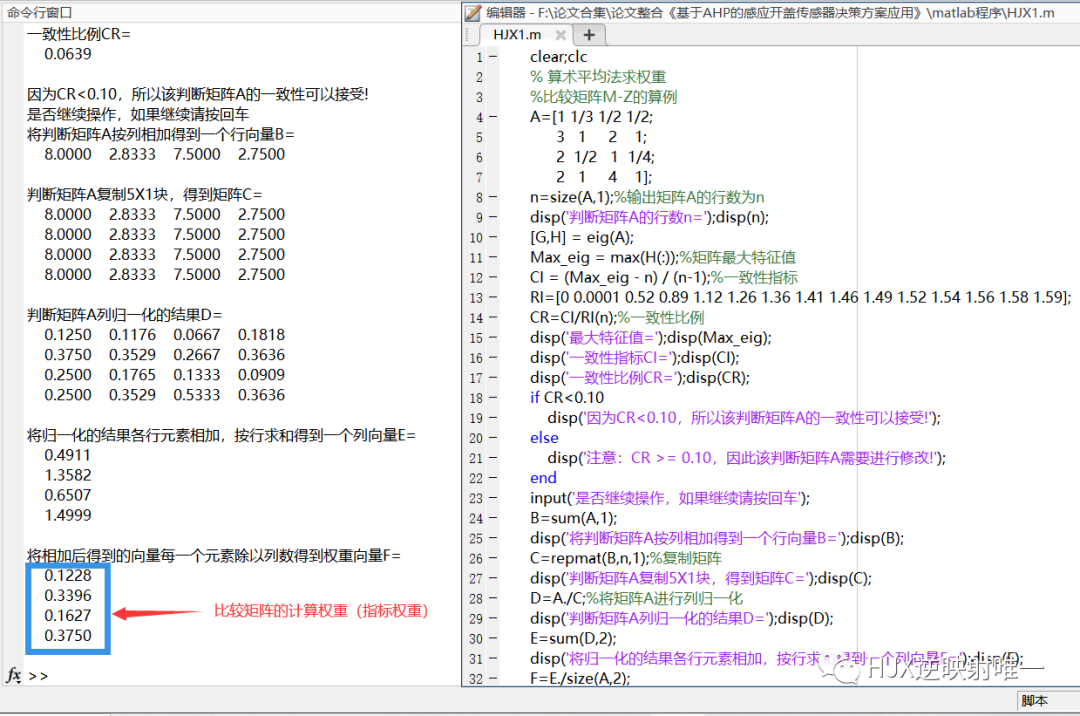
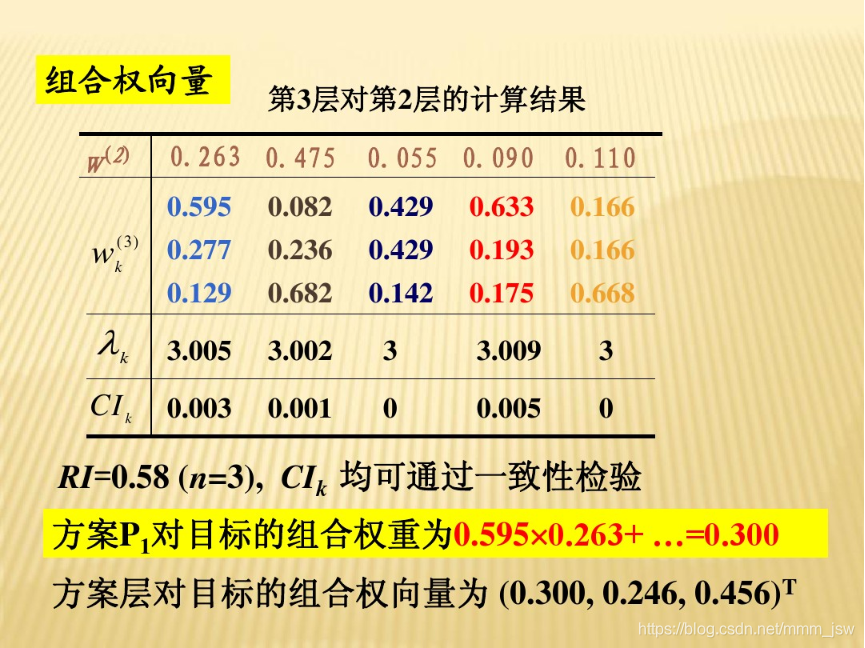
4.汇总结果得到权重矩阵

可以使用EXCEL计算数据

一些局限性

二、代码演示

未完待续

三、模型拓展

1.有多个准则层——一层一层算
2.准则层每个量不对应所有方案——不对应的设为0？
3.只有一个准则层，但是一个准则只对应特定的方案（一对多）