层次分析法（AHP）

1.算法简述与原理分析

​ 层次分析法是一种主观赋值评价方法也是一个多指标综合评价算法，常用于综合评价类模型。层次分析法将与决策有关的元素分解成目标、准则、方案等多个层次，并在此基础上进行定性和定量分析，是一种简单、实用的算法。

​ 原理：是在分析一个现象或问题之前，首先将现象或问题根据他们的性质分解为相关因素，并依据因素之间的关系形成一个多层次的结构模型。然后通过经验或专家来判断低层元素对高层元素的相对重要性，并根据重要性的程度得出权重排序。

2.AHP层次分析法过程

层次分析法进行建模，大致分为以下四步：

1.分析系统中各因素之间的关系，建立系统的递阶层次结构。
2.对于同一层次的个元素关于上一层次中某一准则的重要性两两比较，构造两两比 较矩阵（判断矩阵）。
3.由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验（检验通过权重才能用）。
4.填充权重矩阵，根据矩阵计算得分，得出结果。

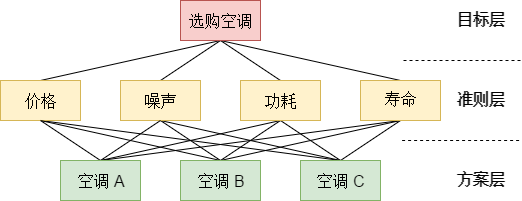
2.1构建层次结构模型

即将所有相关因素分为目标层、准则层和方案层

2.2构造判断矩阵

即把准则层的指标进行两两判断，确定各准则层对目标层的权重

对于准则层A我们可以构建：

q其中A中的元素满足：
$$w_i=\frac{1}{n}\sum _{j=1}^n\frac{a_{ij}}{\sum _{k=1}^n{a}_{kj}},(i=1,2,\dots ,n)\dots \dots \dots \dots \dots （2）$$
矩阵里面写什么简单来说就是假如有三个元素A、B、C，A和B相比A重要多少，A比C中要多少，B比C中要多少，这个“多少”我们通常使用Santy的1-9标度方法给出，即：

2.3层次单排序

大白话说一下，就是求解各个指标的权重。计算方法有三种：算数平均法、几何平均法和特征值法。（小tips：在实际建模中，不同的计算方法可能会导致结果有所偏差，为了保证结果的稳健性，可以采用多种方法分别对权值进行求解，避免单一方法所需产生的误差，使得出的结论更全面有效。）

举个栗子，这是一个判断矩阵。

2.3.1方法1：算术平均法求权重

Step1：将判断矩阵按照列归一化（每个元素除以其所在列的和，如1/（1+1/2+1/4）=0.5882）

Step2：将归一化的列相加（按行求和）

Step3：将相加后的每个元素除以n即可得到对应的权重向量

转换为数学公式就是：

$$w_i=\frac{1}{n}\sum _{j=1}^n\frac{a_{ij}}{\sum _{k=1}^n{a}_{kj}},(i=1,2,\dots ,n)\dots \dots \dots \dots \dots （2）$$

2.3.2方法2：几何平均法求权重（又叫方根法）

举个栗子：

Step1：计算每行乘积的m次方，得到一个m维向量

景色：$\sqrt[5]{1\ast 5\ast 5\ast \frac{1}{3}\ast 8}=2.3162$

费用：$\sqrt[5]{\frac{1}{5}\ast 1\ast \frac{1}{4}\ast \frac{1}{6}\ast 2}=0.4409$

居住：$\sqrt[5]{\frac{1}{5}\ast 4\ast 1\ast \frac{1}{5}\ast 3}=0.8635$

饮食：$\sqrt[5]{3\ast 6\ast 5\ast 1\ast 6}=3.5195$

旅途：$\sqrt[5]{\frac{1}{8}\ast \frac{1}{2}\ast \frac{1}{3}\ast \frac{1}{6}\ast 1}=0.3222$

Step2：把向量标准化即为权重向量，即得到权重

设SUM=2.3162+0.4409+0.8635+3.5195+0.3222

则 景色：2.3162/SUM=0.3104

​ 费用：0.4409/SUM=0.0591

​ 居住：0.8635/SUM=0.1157

​ 饮食：3.5195/SUM=0.4716

​ 旅途：0.3222/SUM

转换为数学公式为：
$$\overline{w_i}=\sqrt[m]{\prod _{j=1}^m{a}_{ij}}\dots \dots \dots \dots （1）$$

$$w_i=\frac{\overline{w_i}}{{\sum }_{j=1}^m\overline{w_j}}\dots \dots \dots \dots （2）$$

2.3.3方法3：特征值法求权重

一致矩阵有一个特征值为n，其余特征值均为0。特征值为n时，对应的特征向量刚好为：
$$k{\left[\frac{1}{a_{11}},\frac{1}{a_{12}},\dots ,\frac{1}{a_{1n}}\right]}^T(k\ne 0)$$
那么我们直接可以将特征向量归一化即可求得权重向量。

2.4一致性检验

2.4.1求解最大特征值

求得权重矩阵后，可以计算最大特征跟，公式为：
$${\lambda }_{\max }=\frac{1}{n}\sum _{i=1}^n\frac{{(AW)}_i}{W_i}$$
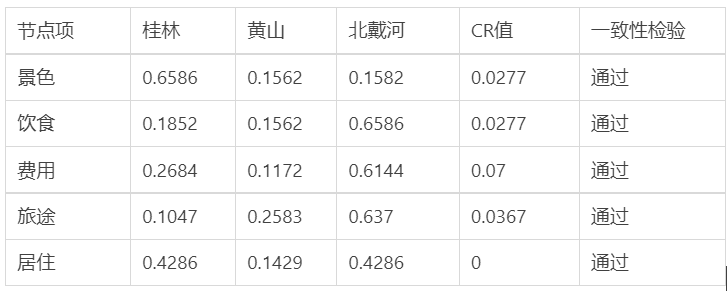
其中n为维度数，例如之前我们举得例子因素为景色、费用、居住、饮食、旅途时，n=5。AW为：判断矩阵*标准化后的权重，然后按行的累加值。

还是举个栗子：

判断矩阵A为：

标准化权重W为：

其中A*W为：(就是对应位置相乘)

AW的值就是按行相加。

则最大特征值为：
$${\lambda }_{\max }=x/n=5.416$$
其中，x=AW1/W1+AW2/W2+…+AWn/Wn。n为矩阵阶数。

2.4.2求解CI、RI、CR值，判断一致性是否通过

Step1：一致性指标CI值的求解公式为：
$$CI=\frac{{\lambda }_{\max }-n}{n-1}$$
将2.4.1的例子代入可得CI=0.1042

Step2：平均随机一致性指标RI值是通过查表得出来的：

将2.4.1的例子代入可得RI=1.12

Step3：计算一致性比例CR：
$$CR=CI/RI$$
将Step1和Step2的计算结果代入可得CR=0.093

Step4：判断是否通过一致性检验：

CR<0.1 时，表明判断矩阵 A 的一致性程度被认为在容许的范围内，此时可用 A 的特征向量开展权向量计算；若 C.R.≥0.1, 说明我们在构建判断矩阵时出现了逻辑错误，需要重新构建判断矩阵。如例题中CR=0.093<0.1，则视为检验合格。

Matlab实现代码（只需要替换判断矩阵即可）

A=[1 2 3 4 5;1/2 1 2 3 4;1/3 1/2 1 2 3;1/4 1/3 1/2 1 2;1/5 1/4 1/3 1/2 1];
%disp('请输入准则层判断矩阵A(n阶)');
%A=input('A=');
[n,n]=size(A);Sum_A=sum(A);
SUM_A=repmat(Sum_A,n,1);
Stand_A=A./SUM_A;
disp('算术平均法求权重的结果为：')
disp(sum(Stand_A,2)./n);Prduct_A=prod(A,2);
Prduct_n_A=Prduct_A.^(1/n);
disp('几何平均法求权重的结果为：')
disp(Prduct_n_A./sum(Prduct_n_A));[V,D]=eig(A);%求得特征向量和特征值%求出最大特征值和它所对应的特征向量
tempNum=D(1,1);
pos=1;
for h=1:nif D(h,h)>tempNumtempNum=D(h,h);pos=h;end
end    
w=abs(V(:,pos));
w=w/sum(w);
t=D(pos,pos);
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
enddisp('请输入方案层各因素对准则层各因素权重的成对比较阵');
for i=1:ndisp('请输入第');disp(i);disp('个准则层因素的判断矩阵B');disp(i);
enddisp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
enddisp('请输入方案层各因素对准则层各因素权重的成对比较阵');
for i=1:ndisp('请输入第');disp(i);disp('个准则层因素的判断矩阵B');disp(i);
end

.
.
.
.
.
.

参考文章：https://mpaidata.blog.csdn.net/article/details/122081827