层次分析法的特点：在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。是对难于完全定量的复杂系统作出决策的模型和方法。

决策是指在面临多种方案时需要依据一定的标准选择某一种方案。

1 层次分析法概述

层次分析法（AHP法）：该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以定量方法解决的课题。

层次分析法是社会、经济系统决策中的有效工具。其特征是合理地将定性与定量的决策结合起来，按照思维、心理的规律把决策过程层次化、数量化。是系统科学中常用的一种系统分析方法。

层次分析法的3大典型应用：

1. 用于最佳方案的选取（选择运动员、选择地址）
2. 用于评价类问题（评价水质状况、评价环境）
3. 用于指标体系的优选（兼顾科学和效率）

2 层次分析法的基本原理

根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最底层（供决策的方案、措施等）相对于最高层（总目标）的相对重要权值的确定或相对优劣次序的排定。

运用层次分析法构造系统模型时，大致分为以下4个步骤：

1. 建立层次结构模型
2. 构造判断（成对比较）矩阵
3. 层次单排序及其一致性检验
4. 层次总排序及其一致性检验

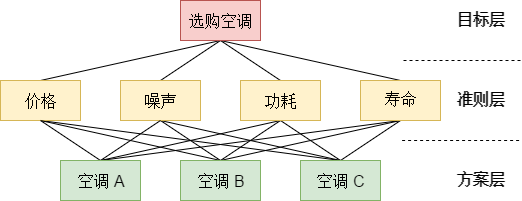
2.1 建立层次结构

将决策的目标、考虑的因素（决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最底层，绘出层次结构图。

一定要绘制出层次结构图！！！

• 最高层：决策的目的、要解决的问题
• 中间层：决策时的备选方案
• 最底层：考虑的因素、决策的准则
• 若只有两层，没有备选方案，最高层为目标层，最底层为因素层

层次分析法的思维过程的归纳：将决策问题分为3个或多个层次

• 最高层（目标层）：表示解决问题的目的，即层次分析要达到的总目标，通常只有一个总目标
• 中间层、准则层、指标层、约束层：表示采取的某种措施、政策、方案等实现预定总目标所涉及的中间环节
• 最底层（方案层）：表示将选用的解决问题的各种措施、政策、方案等，通常有几个方案可选。

例1：大学生就业选择问题

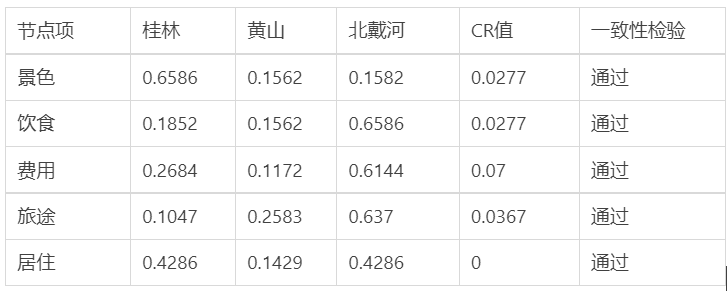
 例2：选择旅游目的地

 2.2 构造判断（成对比较矩阵）

不把所有因素放在一起比较，而是两两相互比较

心理学家认为成对比较的因素不宜超过9个，否则不宜比较，即每层不要超过9个因素。

判断矩阵元素aij的标度方法

 

 注意：值不具有传递性，不成比例

2.3 层次单排序及其一致性检验

 2.4 层次总排序及其一致性检验

• 计算某一层所有因素对于最高层（总目标）相对重要性的权值，称为层次总排序
• 这一过程是从最高层到最底层依次进行的

3 层次分析法的步骤和方法

层次分析法的基本步骤归纳如下：

1.建立层次结构模型：

        包括目标层、准则层、方案层

2.构造成对比较矩阵：

        从第二层开始用成对比较矩阵和1~9尺度

3.计算单排序权向量并做一致性检验

        对每个成对比较矩阵计算最大特征值及其对应的特征向量，利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过，特征向量（归一化后）即为权向量；若不通过，需要重新构造成对比较矩阵。

4.计算总排序权向量并做一致性检验。

        计算最下层对最上层总排序的权向量，利用总排序一致性比率CR进行检验。

4 层次分析法的应用

旅游问题

 

 

 归一化特征向量加起来等于1

 

 

% disp函数会直接将内容输出在Matlab命令窗口中
disp('请输入准则层判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A); % 计算矩阵A的行和列
[V,D]=eig(A);%求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。%求出最大特征值和它所对应的特征向量
tempNum=D(1,1); % 特征值的初值
pos=1;    % 标记的第一个数
for h=1:nif D(h,h)>tempNumtempNum=D(h,h);pos=h;end
end   % 找最大特征值及其对应的位置 
w=abs(V(:,pos));    % 找出最大特征值对应的特征向量
w=w/sum(w);    % 归一化处理
t=D(pos,pos);  % 最大特征值
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10disp('此矩阵的一致性可以接受!');disp('CI=');disp(CI);disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
end

5 应用层次分析法的数学建模案例

选拔优秀参赛队员问题

 

6 层次分析法的优缺点分析

优点：系统性、实用性、简洁性

缺点：具有主观性，结果比较粗超，难以为众人所接受