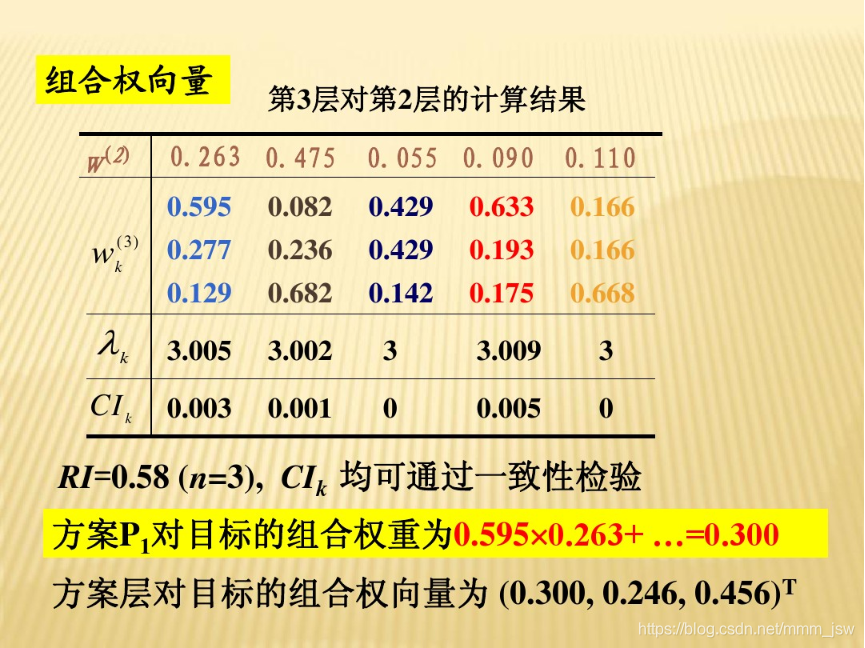
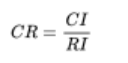目录:
- 层次分析法简介
- 层次分析法基本原理
- 构造判断矩阵
- 一致性检验
- 一致性检验通过的判断矩阵求权重
4.1 算数平均法求权重
4.2 几何平均法求权重
4.3 特征值法求权重- 总结
0. 层次分析法简介
层次分析法(Analytic Hierarchy Process,简称AHP)主要是对于定性的决策问题进行定量化分析的方法。举个例子,在日常生活中,我们经常需要进行感性的判断,比如报高考志愿,感觉清华北大都很好,到底要报哪个;再比如去市场买菜,到底是买青椒做青椒炒鸡蛋,还是买黄瓜做黄瓜炒鸡蛋;再比如想去出游,到底是去公园A还是公园B。上面提到的这些问题,都是决策,也叫做评价类问题,最终的目的就是要评价到底哪个更好。这个方法在数学建模比赛,比如美赛等比赛中有时会用到,另外对日常的生活也有一定的指导。
那么如何用数学的评价体系去解决这类看似非常感性的问题呢,这就诞生了我们今天要讲的层次分析法。这里我们从浅入深对于层次分析法进行一个讲解。
1. 层次分析法基本原理
这里我们举一个例子让大家大致的了解层次分析法的基本原理。假如,小明想买一瓶饮料喝,他在纠结到底是买可乐好,还是雪碧好,还是汇源果汁,他非常的纠结,于是想建个模型来分析到底买哪种饮料好。
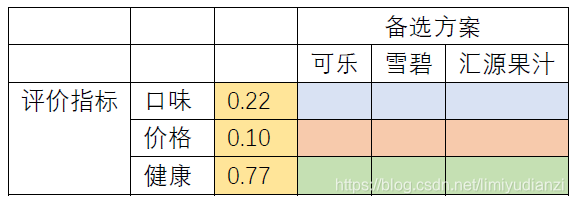
为了实现这个评价,首先我们要确定评价的指标,比如这里我们设定三种指标:饮料的口味,饮料的价格和饮料健康程度,那么最直观的量化方法就是给各个因素一个权重,然后给各个饮料进行打分,如下表:
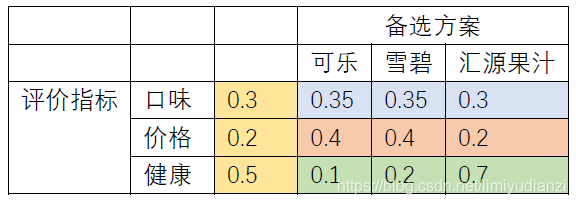
表格中相同颜色的区域加和需要为1,这是为了标准化。所以我们来看一下这个表格,在评价指标方面,小明很注重健康因为给了健康0.5的权重,其次是口味0.3,最后是价格0.2; 具体的在口味方面,小明觉得可乐和雪碧差不多(0.35),果汁稍微差一点是0.3 以此类推,小明就只做了这张表格,为了计算每种饮料的得分,我们只需要把备选方案的权重乘对应的评价指标的权重并且加和即可,也就是:
可乐的最终得分是0.35×0.3+0.4×0.2+0.1×0.5 = 0.1005;
雪碧的最终得分是 0.35×0.3+0.4×0.2+0.2×0.5 = 0.1505;
汇源果汁的最终得分是 0.3×0.3+0.2×0.2+0.7×0.5 = 0.379;
通过比大小我们就看得出来汇源果汁的最终得分最高,所以小明应该选择汇源果汁。
回顾一下,为了量化的评价,我们需要确定评价指标,和备选方案两个重要的因素,接着分配权重(记得加和为1),最终通过乘法然后加和的方式得到最终的量化得分,从而做出最终的评价。
2. 构造判断矩阵
层级分析法就是简单的编造几个权重然后进行抉择么?当然不是,如何客观合理的设定表格中的权重才是重中之重,因此,我们这里介绍如何构造判断矩阵。
在现实问题中,往往存在很多个评价指标,让小明从饮料的口味,价格,健康,瓶盖能不能兑奖,瓶子是不是好看,自己是不是汇源果汁的代言人……等很多评价指标中给出合理的权重是一个非常困难的事情,也许小明现在给出的权重和一会儿给出的权重就完全不同,所以,为了简化思维过程,我们首先进行评价指标的两两比较,再将比较结果汇总成最终的权重。
为了量化两两比较的结果,我们要祭出一个评价体系表格(不要问我从哪里来~它的故乡在远方)说白了,就是在A和B两者比较中划分了一个1到9的重要等级。
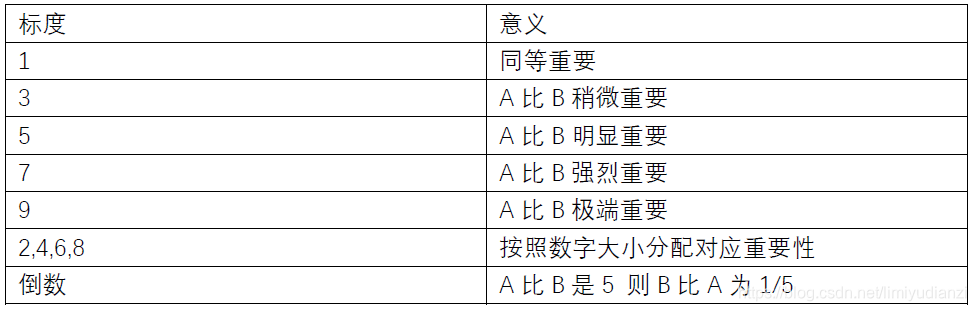
举个例子,假如说饮料的健康性(A)和口味(B)相比,健康要明显重要,则我们就可以说A比B的权重是5。之后我们开始构建我们的判断矩阵。
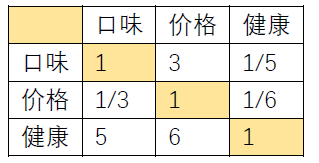
上述的表格就是一个判断矩阵,我们可以看到这个判断矩阵有几个特点,对角线都为1,而且对角线对称的元素相乘都为1,这样的矩阵也被称为正互反矩阵。
为了更加数学的描述,我们设定矩阵的元素定义为a_ij代表了与j相比i的重要性,其中i表示行,j表示列, 其中a_ij>0而且a_ij×a_ji=1即对称元素相乘为1。当i=j时,也就是元素在对角线上时,元素为1。另外理想的情况下要满足a_ij=a_ik×a_kj 这个理想的条件我们在以后说明
在构造判断矩阵的过程中我们的元素是两两进行判断的,所以是不是有可能出现问题呢?答案是有可能的,我们将表格中的元素进行一个更改,并用绿色标记出,随后得到了如下的表格
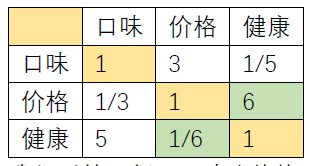
我们看第一行,口味比价格重要(口味>价格)同时健康比口味重要(健康>口味),那么按照正常的推理我们是不是应该得到健康比价格重要(健康>口味>价格)然而实际上表格中填写的是价格比健康重要(价格>健康)这就出现了矛盾,也就是不一致现象。在理想情况下,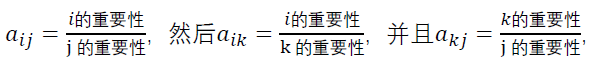
,所以说,在理想的情况下a_ij=a_ik×a_kj 。理想的情况下的判断矩阵也有一些很好的性质,比如行列成比例,也就是说矩阵的秩为1,这里不进行深入的讨论。但是大部分的情况下,没办法达到如此的完美,那么为了量化评价这种不一致现象的大小,就需要在运算权重之前进行一致性的检验。
回顾一下,为了更合理的得到层次分析法表格中的权重,我们引入了数值为1-9的标度体系,并且用两两比较的方法构建了一个判断矩阵用于之后的权重计算,然而判断矩阵存在不一致的问题,因此我们要从数值的角度评价不一致的大小,以此引出一致性的检验。
3. 一致性检验
为了构建一个一致性的指标来验证矩阵的一致性,学者们主要参考了线性代数中的两个定理:
定理1:若A为一致性矩阵,则A的最大特征值λ_max = n,其中n为矩阵A的阶,A的其余特征值均为0。
定理2:n阶正互反矩阵为一致性矩阵,当且仅当其最大特征值λ_max = n,并且当正互反矩阵非一致时,必有λ_max > n。
从定理2的后半句中,我们可以看到,当一个正互反矩阵为非一致的矩阵的时候必有最大的特征值大于矩阵的阶,所以就想到可以使用最大特征值和矩阵的阶的差值来定义不一致性。这种想法看似复杂,其实超级朴素,比如时间不能倒流,所以出生后经过的年数就定义为你的年龄(年数-0)。
为此就定义了一致性指标CI,CI = (λ_max – n) / (n -1)。也就是说一致性指标CI越大,整个矩阵就越不一致,当CI是0的时候是完全理想的一直矩阵。(难道这不应该叫不一致性指标么???)
另外,为了得到计算出来的一致性指标到底是大还是小,我们又构建了平均随机一致性指标RI,该指标的构建方法是随机构建1000个正互反矩阵,并计算一致性指标的平均值。这里的RI也就是说当矩阵的阶数为n的时候随机的平均一致性。这相当于一把尺子,告诉大家如果完全随机(瞎蒙)的填写这个判断矩阵的结果的话,那么你的一致性指标的期望就大概是这个RI的值。RI如何计算呢?查表就可以了。

当CI和RI的比值小于0.1的时候,我们认为这个矩阵是一致的,也就是说你矩阵的一致性指标,要比平均的瞎蒙的一致性指标小一个数量级的时候,我们认为你就不是乱猜的了。这样我们就构建了我们的一致性比例CR = CI/ RI。如果说一个正互反矩阵的一致性比例没有小于0.1,那么就需要调整矩阵以满足要求。
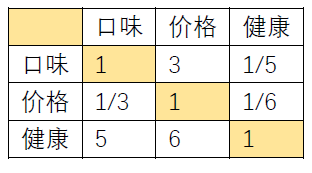
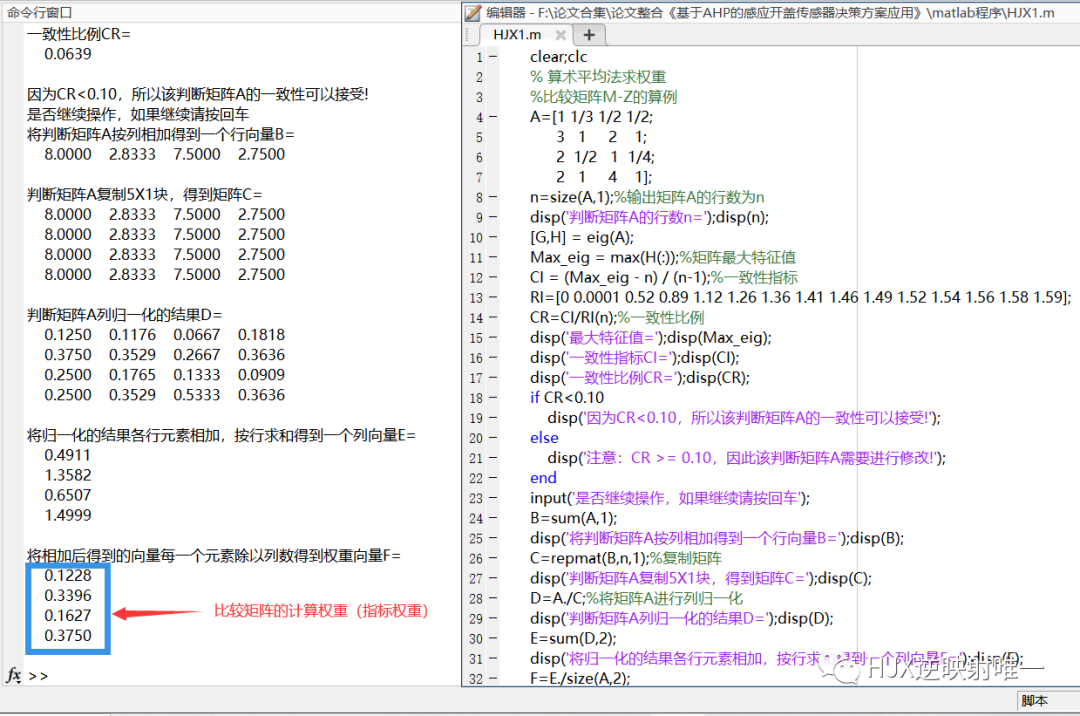
举个例子,我们以这个判断矩阵为例,计算它是否满足一致性的要求,第一步是计算其最大的特征值,在matlab中,我们可以使用[x,y] = eig([1,3,1/5;1/3,1,1/6;5,6,1]); l_max = max(diag(y)); 计算得到,最后计算得到的最大特征值为3.0940, 我们可以看到这个值满足我们定理2中所说的要比矩阵的阶数3大。CI = (l_max -3) / ( 3 -1 ); 计算CI值是0.0470。RI值通过查表得到是0.52,最后我们的RI值就是CI/RI = 0.0904 < 0.1 所以这个矩阵满足一致性的要求。
回顾一下,这里主要讲如何验证矩阵的一致性,为了验证一致性构造了一致性比例CR,满足CR小于0.1的就认为该判断矩阵合理,不满足的就要对判断矩阵进行调整,得到合理的判断矩阵,得到合理的判断矩阵之后,就可以进行最初的,层次分析法的计算了。
4.一致性检验通过的判断矩阵求权重
得到了合理的判断矩阵我们这里就要计算每个影响因素所占的权重,这里主要有三种方法,算数平均法,几何平均法,和特征值法求权重
4.1 算数平均法求权重:(列归一化,行平均值)
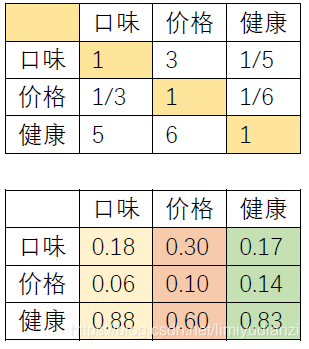
对每列进行归一化处理,并且按照行求平均值就得到了我们最终的权重,这是最简单的计算方法,具体的方法如下:step1:列归一化,
最左上角的元素归一化就是1/(1+1/3+5)=0.18;
第一行第二个元素的计算方法就是3/(3+1+6)=0.30以此类推;
Step2:行平均值:
口味:(0.18+0.30+0.17)/3 = 0.22;
价格:(0.06+0.10+0.14)/3 = 0.10;
健康:(0.88+0.60+0.83)/3 = 0.77;
正常权重的加和是1,这里因为四舍五入的原因有一定的偏差。得到了权重之后,我们就可以写入最开始的表格了(还记得嘛?在算了这么多之后一定要牢记使命,别忘了最开始计算这些东西的目的是什么)
4.2 几何平均法求权重:(行相乘开n次方,列归一化)
这里的计算方法就是将行的元素都相乘,然后再开对应的n次方,并对得到的n个数字进行归一化即可。
4.3 特征值法求权重:(最大特征值的特征向量归一化)
特征值法其实是应用最多的一个方法,就是求最大特征值所对应的特征向量并进行归一化处理,matlab的计算方法如下:[x,y] = eig([1,3,1/5;1/3,1,1/6;5,6,1]); vec_max = x(:,1);得到的vec_max就是最大特征值对应的特征向量了。在本例中是0.26,0.12,0.96在对其进行归一化的处理,得到0.19,0.09,0.72 这样我们就用另一种方法求得了权重。
回顾一下这里介绍了三种不同的方法对判断矩阵的权重进行计算。除了这三个影响因素的判断矩阵以外,具体的表格中可乐,雪碧和汇源果汁的判断矩阵构造方法也是一样的。只需要列出以下的表格,检验一致性并最终计算即可。
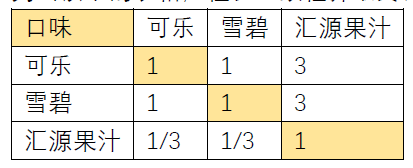
5. 总结
以上就是层次分析法的全部过程,有几个小的问题需要进一步的讲解,当判断矩阵不满足一致性的时候我们调整的方法就是重新梳理整个矩阵的各个元素,可以利用理想状态下,行和列的元素成比例的性质进行微调。另外,层次分析法考虑的因素不能过多,不论是候选的种类,还是评价的指标都不能太多。除此之外,层次分析法主要是在主观的评价体系中进行决策,或者满意度的评价,当在一个问题中,已经有很多已知的数据的时候,这种方法就显得不太好了。