层次分析法(AHP)原理应用及代码
- 1.AHP算法步骤
- 2.算法举例
- 第一步:建立递阶层次图
- 第二步:建立判断矩阵
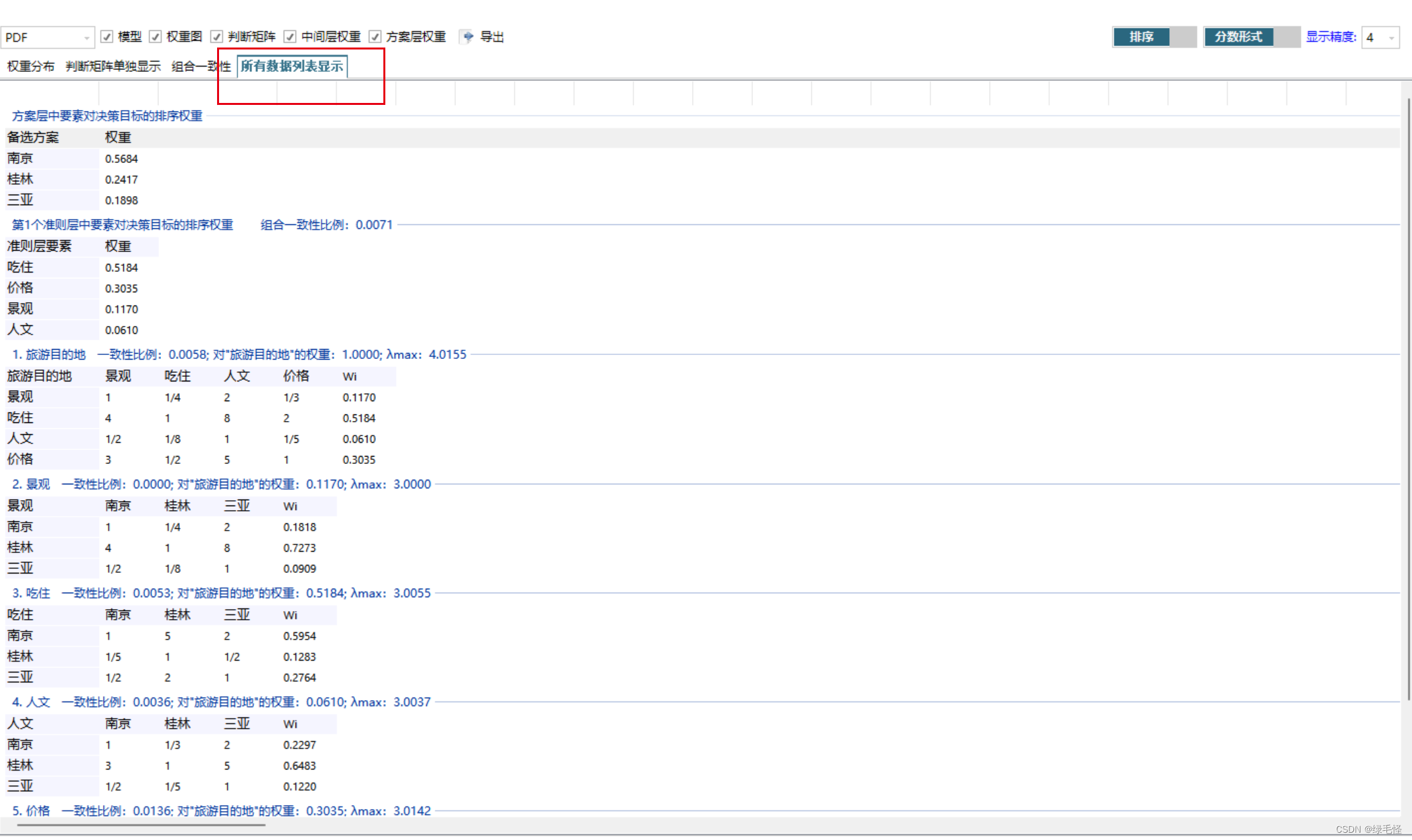
- 计算五个指标的判断矩阵
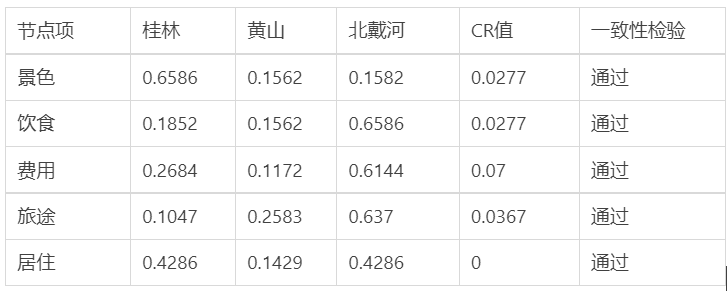
- 计算三个方案相对于某一指标的权重
- 第三步:进行一致性检验
- 一致性检验的步骤
- 第一步:计算一致性指标 C I CI CI
- 第二步:查找对应的平均随机一致性指标 R I RI RI
- 第三步:计算一致性比例 C R CR CR
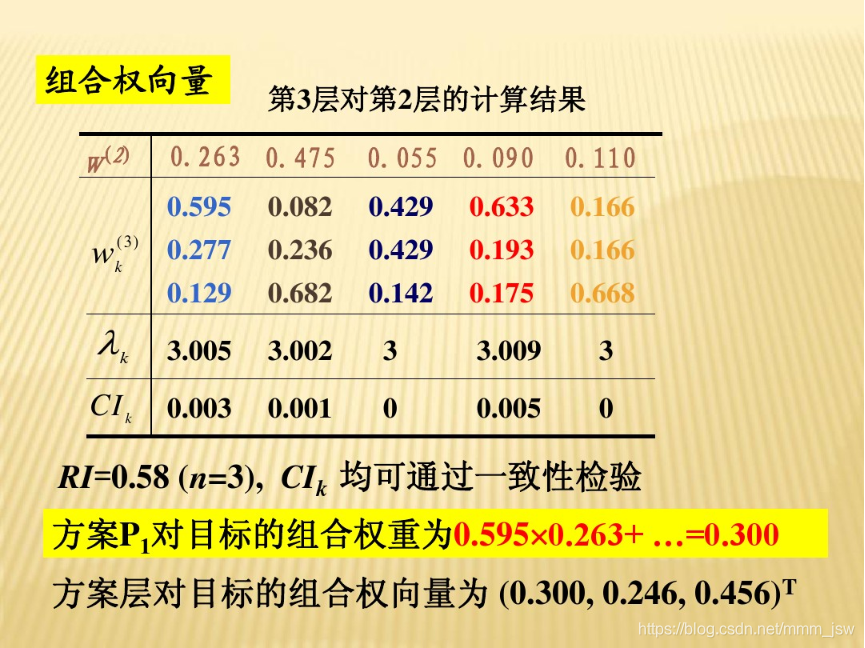
- 第四步:计算权重
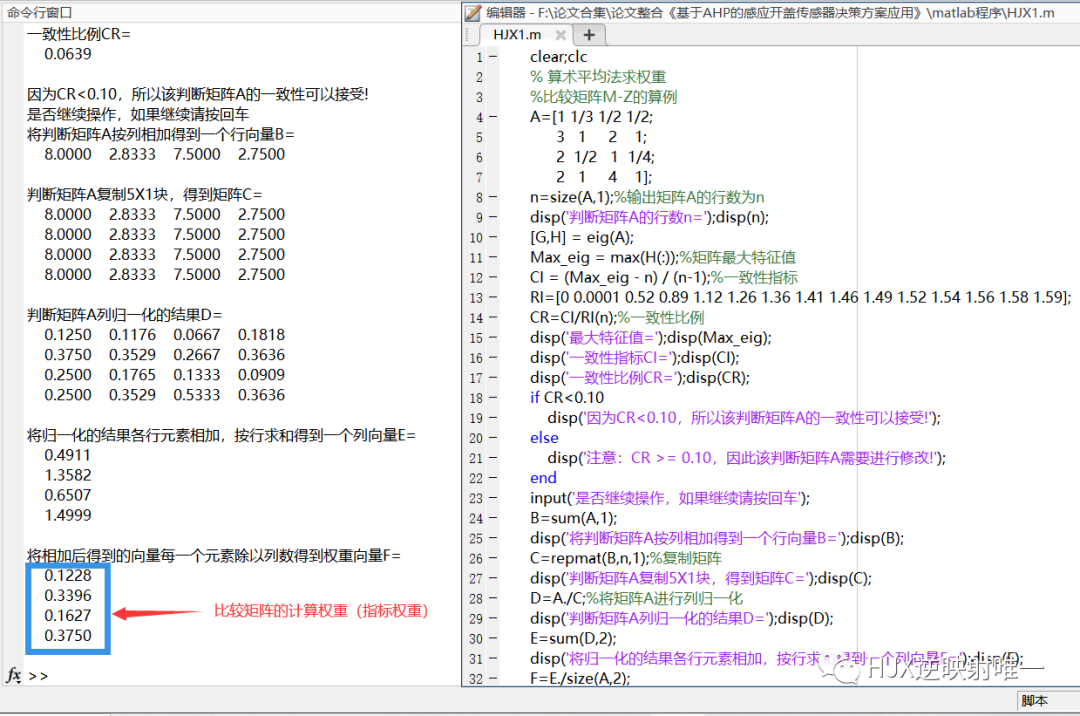
- 第一种:算术平均法
- 第一步:将判断矩阵按照列归一化
- 第二步:将归一化的各列相加(按行相加)
- 第三步:将相加后得到的向量中的每个元素除以 n n n即可得到权重向量
- 第二种:几何平均法
- 第一步:将A的元素按照行相乘得到一个新的列向量
- 第二步:将新的向量的每个分量开n次方
- 第三步:对该列向量进行归一化即可得到权重向量
- 第三种:特征值法
- 第一步:求出矩阵A的最大特征值以及其对应的特征向量
- 第二步:对求出的特征向量进行归一化即可得到我们的权重
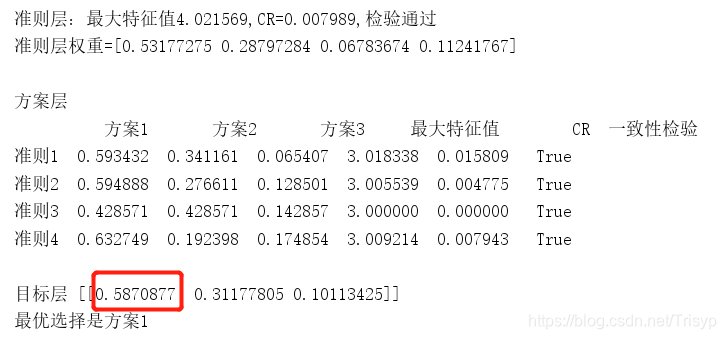
- 第五步:计算方案得分
- 3.模型注意事项(一致性检验不通过怎么办)
- 1. C R < 1 CR<1 CR<1如何修正?
- 2.判断矩阵写法
- 3.平均随机一致性指标 R I RI RI
- 4.如果准则层与方案层不是全连接该怎么办
- 4.模型局限性
- 1.评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大, n n n最多是15
- 2.这是一个将定性分析转化为定量分析的方法,如果决策层中的数据是已知的,则最好不要用层次分析法,可以选用[Topsis方法](https://blog.csdn.net/weixin_44598996/article/details/108804485)
- 5.模型代码
层次分析法是将 定性问题定量化处理的一种方法。
层次分析法简称AHP,其主要特点是通过建立递阶层次结构,把人的主观判断转化为对若干两两因素重要程度的判断上,从而把难以操作的定性判断量化为可操作的重要性程度判断上
1.AHP算法步骤
第一步:分析系统各因素之间的关系,建立递阶层次结构
第二步:对于同一层次的各要素,针对上一准则层的某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)
第三步:根据判断矩阵得到各元素针对于某一准则的相对权重,并进行一致性检验(通过一致性检验的才可使用)
第四步:根据权重矩阵计算得分,并进行排序
2.算法举例
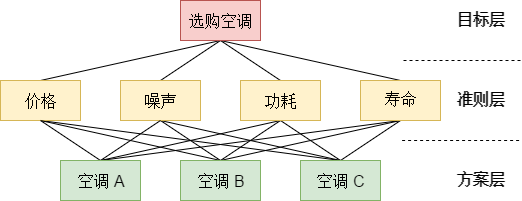
小明同学要出去旅游,事先确定了三个地方,分别是北戴河、苏杭、桂林,但最终无法从这三个地方中选定,希望你通过层次分析法来帮助小明进行判断。
根本目的就是为了填完下面的这张表。用*指标权重*乘以每个地方的得分,然后做和就可以得到这个地方的分数,最后根据分数判断即可

第一步:建立递阶层次图

第二步:建立判断矩阵
因为我们一次性比较五个指标很困难,两两指标进行比较,根据比较的结果确定权重,我们有如下的标准

计算五个指标的判断矩阵
%% 判断矩阵一般交给专家填写,但建模比赛中一般自己判断

(1) a ( i , j ) a_(i,j) a(i,j)表示的意义是,与指标𝑗相比,𝑖的重要程度。
(2)当𝑖 = 𝑗时,两个指标相同,因此同等重要记为1,这就解释了主对角线元素为1。
(3)
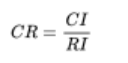










![iOS “[App] if we're in the real pre-commit handler we can't actually add any new fences due](https://img-blog.csdn.net/20161028160636902?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)