AHP层次分析法

article/2025/9/12 5:07:19

层次分析法（Analytic Hierarchy Process，简称 AHP）是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。

层次分析法的基本步骤

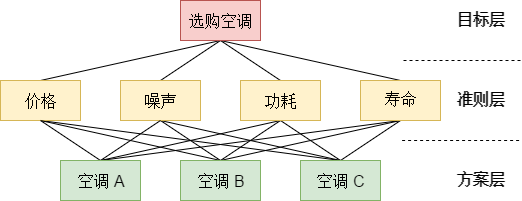
建立递阶层次结构

（1）目标层：这一层次中只有一个元素，它是分析问题的预定目标。

（2）准则层：它可以由若干个层次组成，包括所需考虑的子准则。

（3）方案层：这一层次包括了为实现目标可供选择的各种决策方案等。

例如有华为、小米、vivo,三个手机品牌供你选择，试确定一个最好品牌。在此问题中，你会根据售价、像素、售后服务、差评率、电池等一些准则去反复比较这三个品牌，可以建立如下图1的层次结构模型

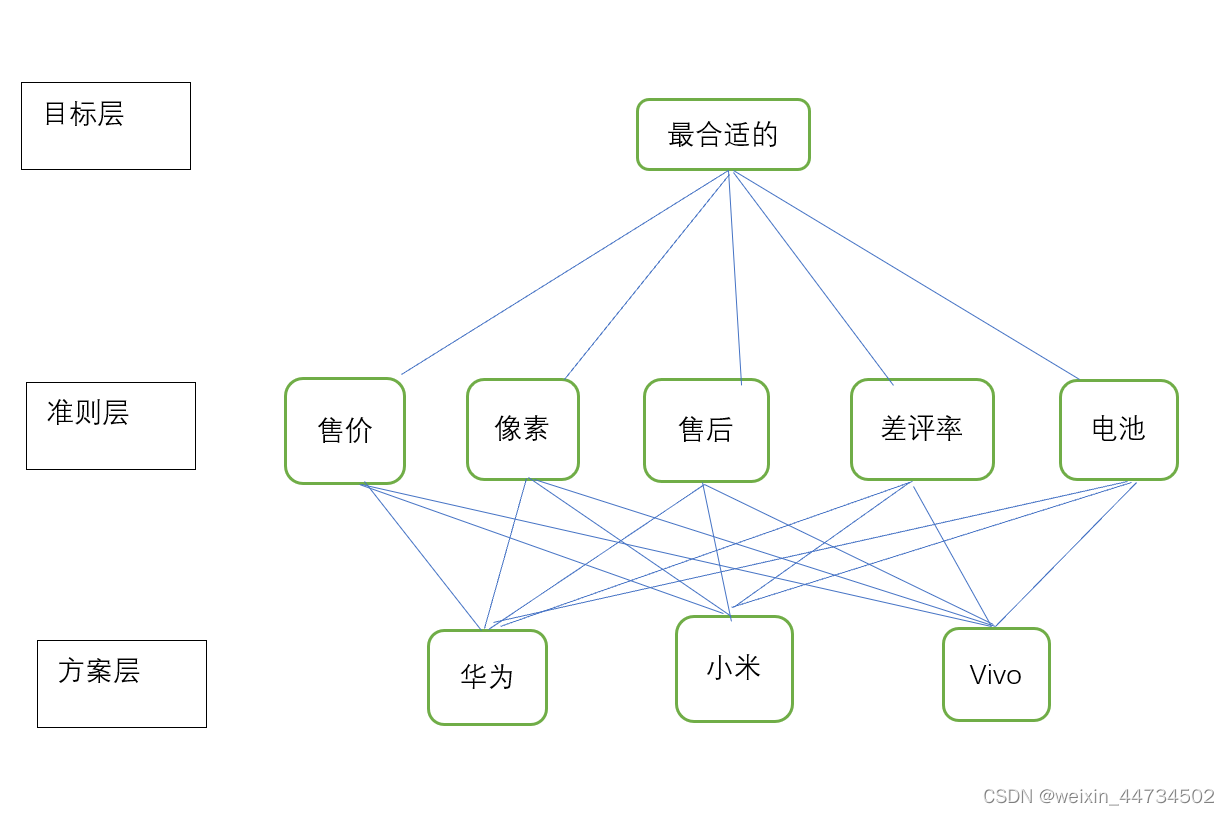
图1 层次结构模型

构造判断矩阵

层次结构反映了因素之间的关系，但准则层中的各准则在目标衡量中所占的比重并不一定相同，在确定影响某因素的诸因子在该因素中所占的比重时，遇到的主要困难是这些比重常常不易定量化。

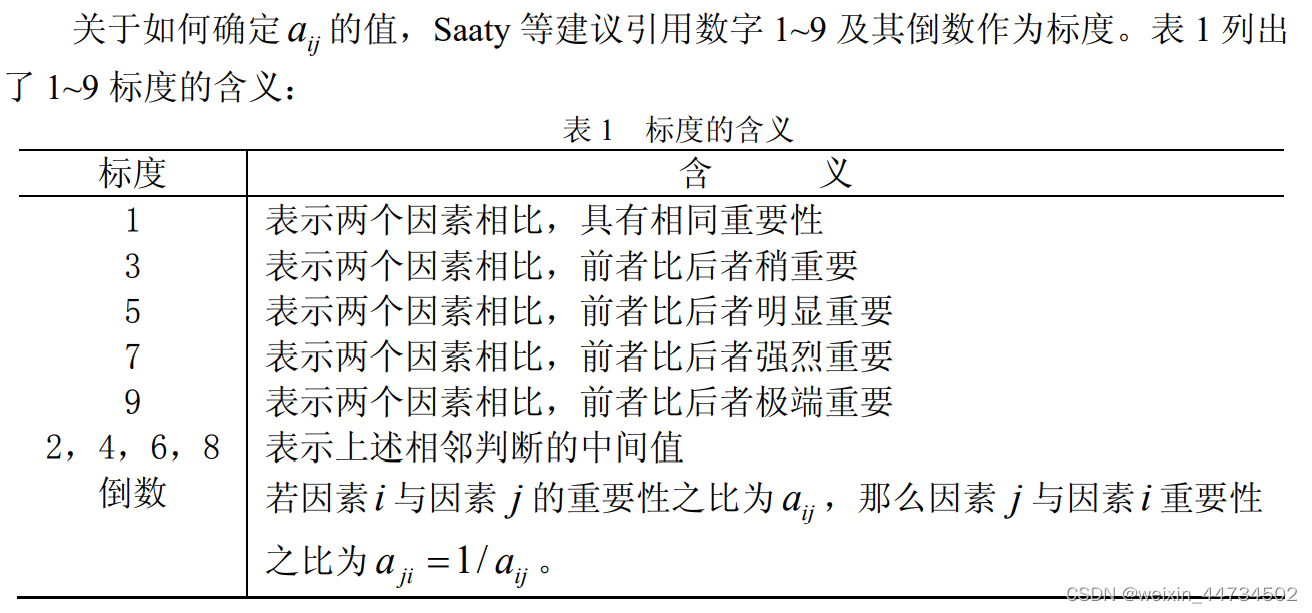
现在要n个因子对某因素Z的影响大小，可以采取对因子进行两两比较建立成对比较矩阵的办法，具体做法是每次取两个因子 $x_{i}$ , $x_{j}$ ,如果 $x_{i}$ 相比 $x_{j}$ 对Z的重要程度为 $a_{ij}$ ,那么 $x_{j}$ 相比 $x_{i}$ 对Z的重要程度为 $a_{ji}=\frac{1}{a_{ij}}$ .关于两个因子的重要程度可根据查找文献等方法获得。

一致性检验

计算一致性比例 $CR$

先计算

$CI=\frac{\lambda _{max}-n}{n-1}$ ,

其中 $\lambda _{max}$ 为判断矩阵的最大特征值，n是判断矩阵行数

$CR=\frac{CI}{RI}$ ,

其中 $RI$ 为平均随机一致性指标，可以查表得到,

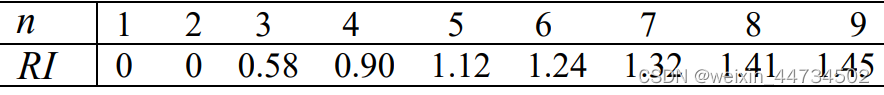
若计算出一致性比例 $CR$ 为0，则判断矩阵是一致矩阵，若 $CR<0.1$ ,那么认为判断矩阵与一致矩阵差别不大，可以通过一致性检验，如果 $CR<0.2$ ,需要修改一致性矩阵。

算术平均法求权重

将通过了一致性检验的判断矩阵按列归一化每一行分别求和，求和的结果除以𝑛 ，得到的列向量就是权重向量

应用实例

挑选合适的工作。经双方恳谈，已有三个单位表示愿意录用某毕业生。该生根据已有信息建立了一个层次结构模型，如图所示。

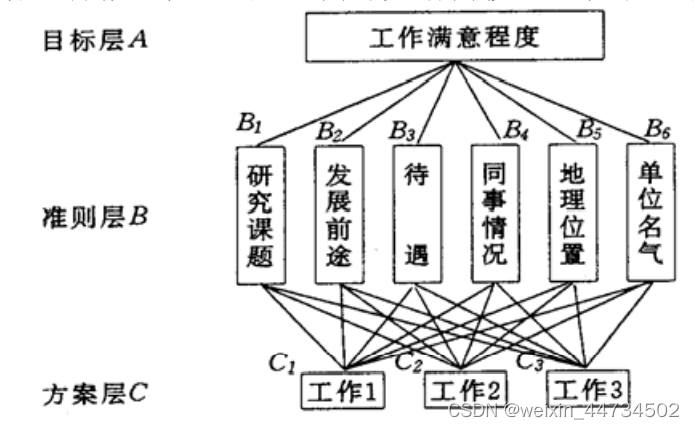
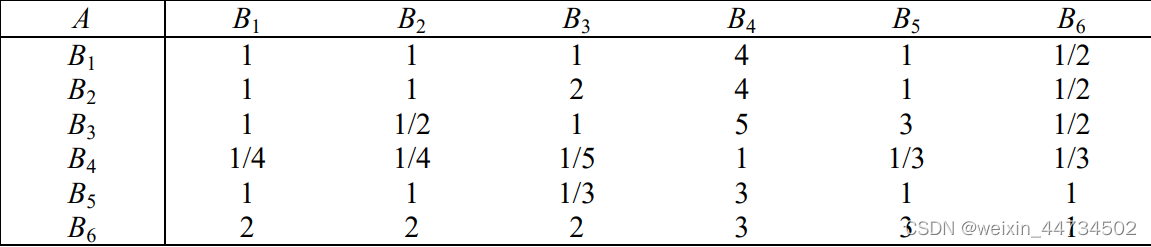
准则层判断矩阵为

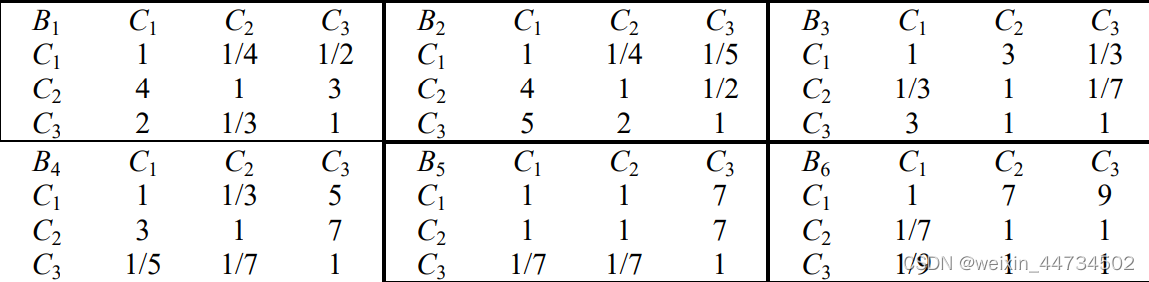
方案层的判断矩阵为

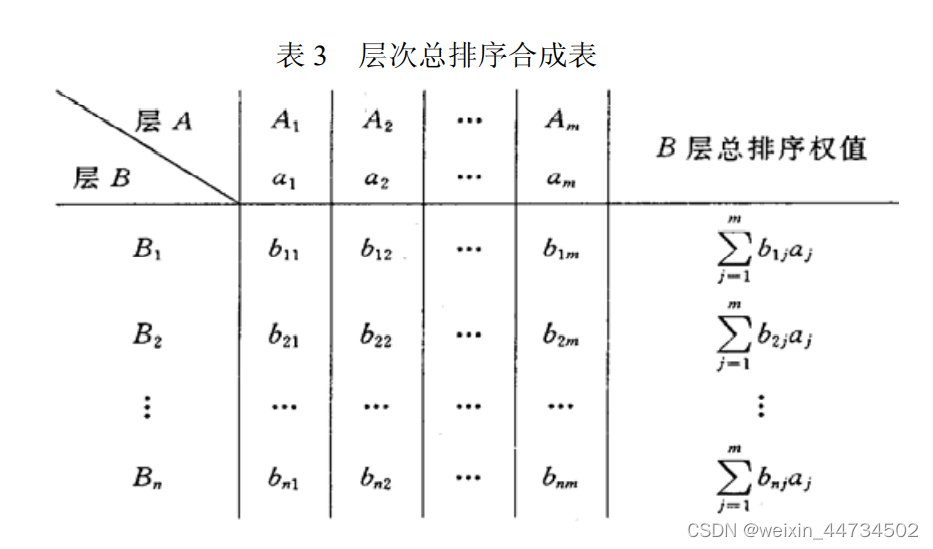
层次总排序的结果

根据层次总排序权值，该生最满意的工作为工作 1。

代码

clc,clear 
fid=fopen('1.txt','r'); 
n1=6;n2=3; 
a=[]; 
for i=1:n1 tmp=str2num(fgetl(fid)); a=[a;tmp]; %读准则层判断矩阵
end 
for i=1:n1 str1=char(['b',int2str(i),'=[];']); str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']); eval(str1); for j=1:n2 tmp=str2num(fgetl(fid)); eval(str2); %读方案层的判断矩阵end 
end 
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a); 
lamda=max(diag(y)); 
num=find(diag(y)==lamda); 
w0=x(:,num)/sum(x(:,num)); 
cr0=(lamda-n1)/(n1-1)/ri(n1) 
for i=1:n1 [x,y]=eig(eval(char(['b',int2str(i)]))); lamda=max(diag(y)); num=find(diag(y)==lamda); w1(:,i)=x(:,num)/sum(x(:,num)); cr1(i)=(lamda-n2)/(n2-1)/ri(n2); 
end 
cr1, ts=w1*w0, cr=cr1*w0% 1.txt
1 1 1 4 1 1/2 
1 1 2 4 1 1/2 
1 1/2 1 5 3 1/2 
1/4 1/4 1/5 1 1/3 1/3 
1 1 1/3 3 1 1 
2 2 2 3 3 1 
1 1/4 1/2 
4 1 3 
2 1/3 1 
1 1/4 1/5 
4 1 1/2 
5 2 1 
1 3 1/3 
1/3 1 1/7 
3 7 1 
1 1/3 5 
3 1 7 
1/5 1/7 1 
1 1 7 
1 1 7 
1/7 1/7 1 
1 7 9 
1/7 1 1 
1/9 1 1