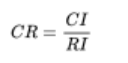一·、模型介绍

  层次分析法（AHP）是美国运筹学家萨蒂于上世纪70年代初，为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。
  层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题。

二、模型原理

1.构建模型的框架

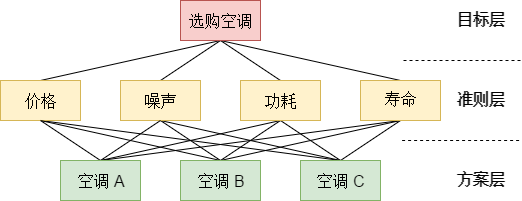
以旅游地选择层次结构图为例：

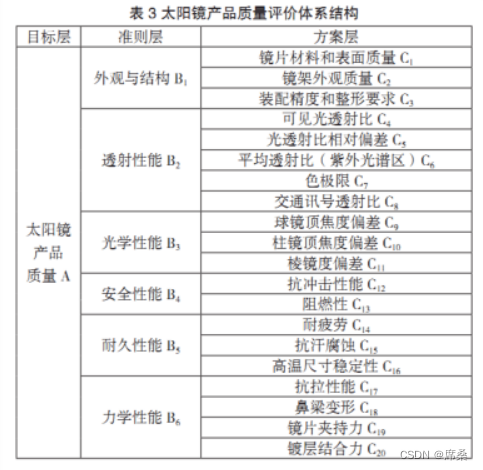
 首先我们要将问题分解，逐层分析各因素之间的层进式关系，再分别确定目标层、准则层与方案层之间对应的元素。

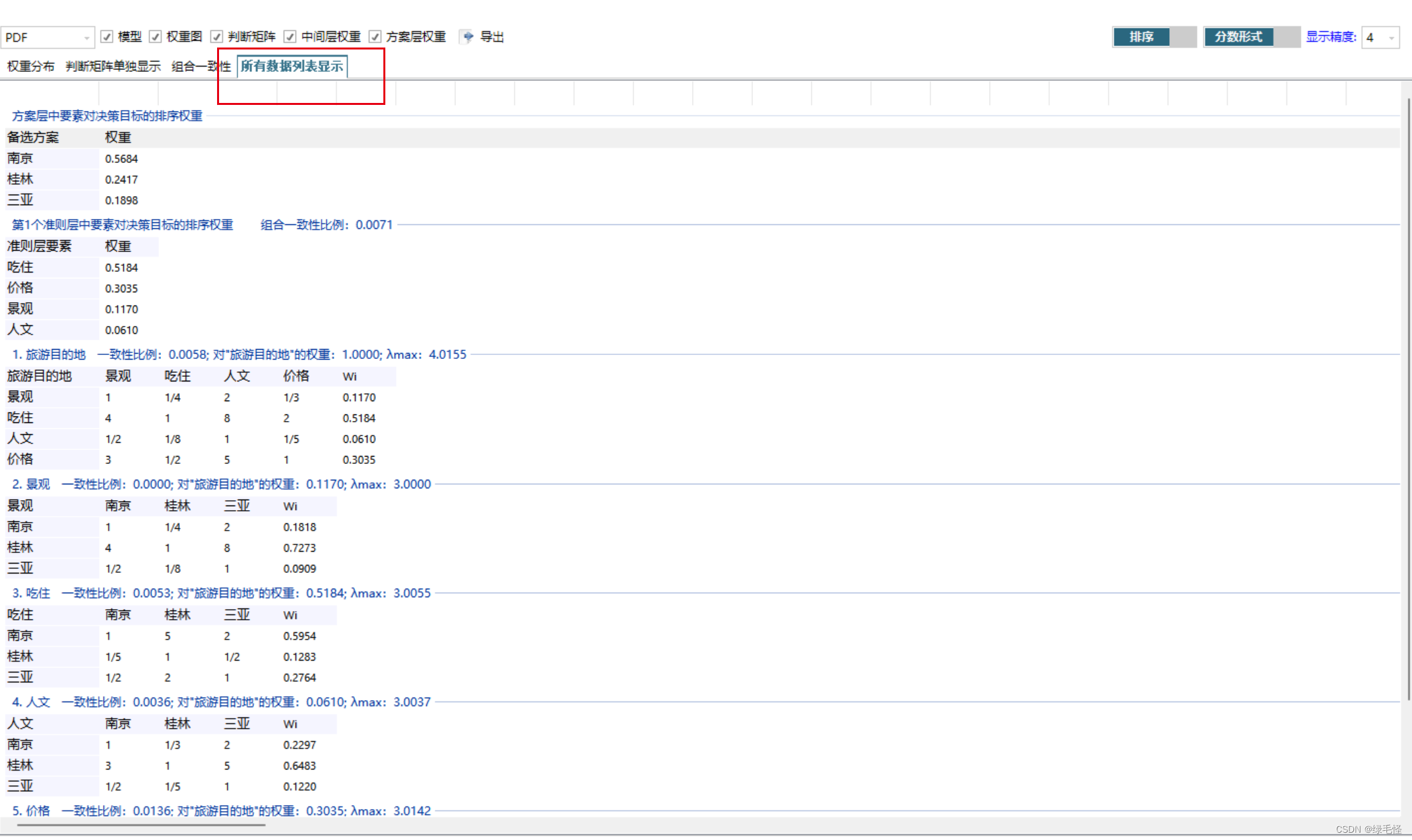
2.构造判断矩阵

对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造判断矩阵：

 判断矩阵具有一定程度上的主观性，需要使用者多查阅相关权威文章与专家建议再做判断矩阵。

3.一致性检验

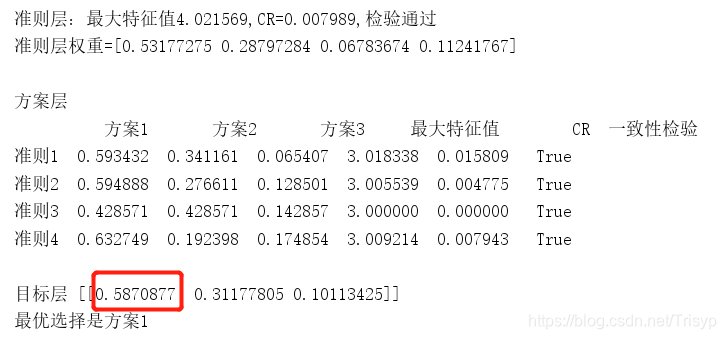
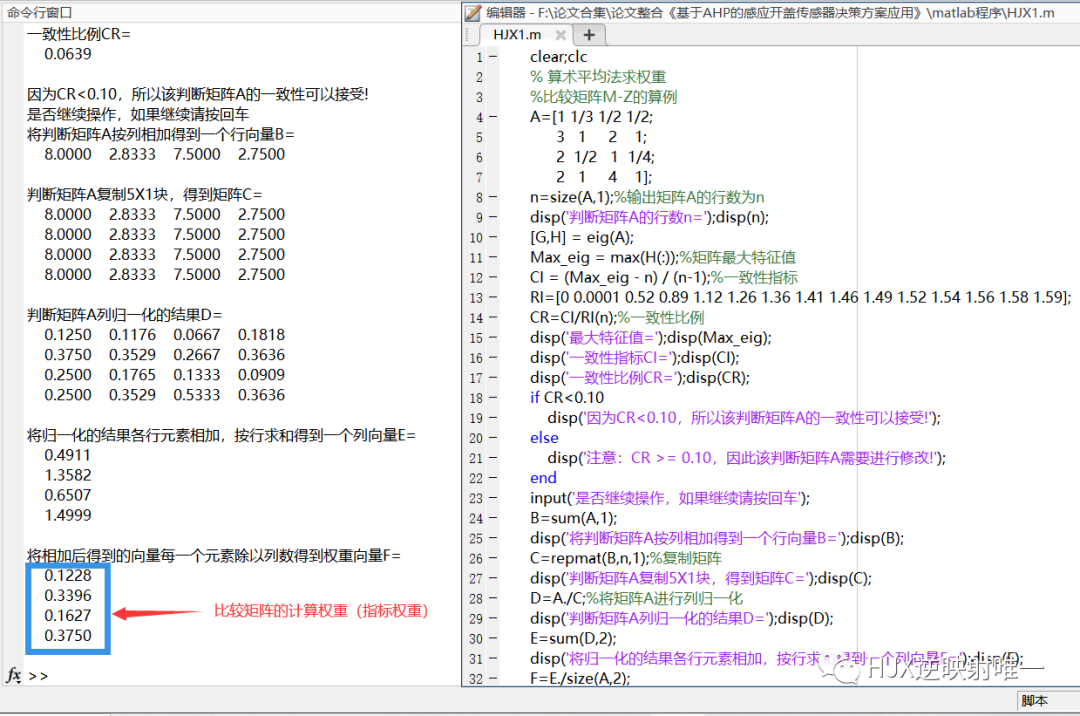
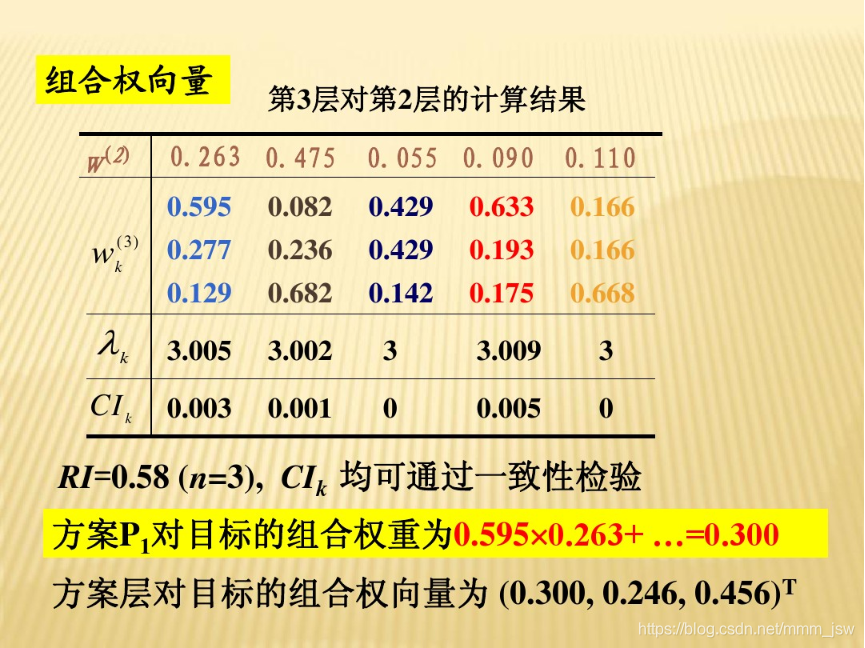
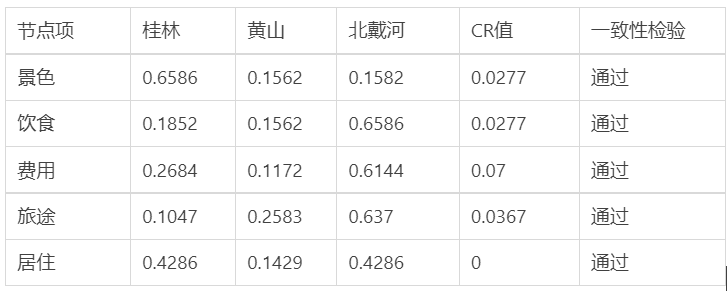
3.1在进行一致性检验之前，我们先要计算由判断矩阵被比较元素对于该准则的相对权重。可以用算术平均法、几何平均法与特征值法计算权重。

接下来就要进行一致性检验了

3.2将判断矩阵进行归一化，计算一致性指标CI：

 3.3查找对应的平均随机一致性指标RI：

（一般n值不大于15，若n值过大会导致模型产生误差 ）

3.4计算一致性比例CR：

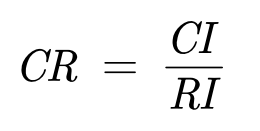
 若CR<0.1，则可认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正（尽量使判断矩阵各行成倍数关系~）。

注意！！若模型未通过一致性检验则无法使用

4.计算得分并排序

 这样我们就可以用层次分析法得出我们想要的结果啦

三、算法应用

  应用领域：经济计划个管理，能源政策和分配，人才选拔和评价，生产决策，交通运输，科研选题，产业结构，教育，医疗，环境，军事等。

  处理问题类型：决策、评价、分析、预测等。

  建立层次分析结构模型是关键一步，要有主要决策层参与。

  构造成对比较矩阵是数量依据，应由经验丰富、判断力强的专家给出。