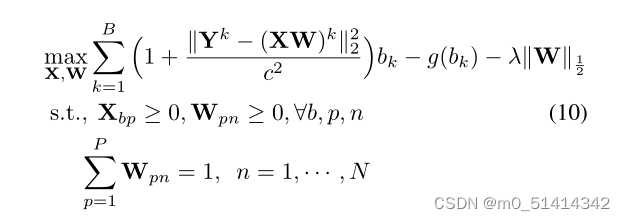J. Peng, F. Jiang, W. Sun and Y. Zhou, "Cauchy NMF for Hyperspectral Unmixing," IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium, 2020, pp. 2384-2387, doi: 10.1109/IGARSS39084.2020.9323950.

摘要：

非负矩阵分解(Non-negative matrix factorization, NMF)是一种经典的高光谱解混模型，它使高光谱数据矩阵与其低秩近似(即端元矩阵和丰度矩阵的乘积)之间的欧氏距离最小化，但由于损失函数对异常值很敏感，因此在应用于有噪声数据时失效。本文提出了一种用柯西损失函数(CLF)代替传统最小二乘损失的高光谱解混柯西NMF (CauchyNMF)模型。与最小二乘损失相比，CLF可以对噪声项进行惩罚，抑制真实数据中混合的大噪声，因此具有更强的鲁棒性。在模拟高光谱数据集和真实高光谱数据集上的实验结果表明，本文提出的CauchyNMF方法比现有的NMF方法更准确、更鲁棒，特别是在噪声较大的情况下。

背景：

为了使结果在物理上有意义，通常对每个像素的丰度向量施加和对一的约束。此外，为了提高解混性能，还在NMF框架中加入了许多其他约束，如端元[6]上的最小体积约束，丰度矩阵[3]上的ℓ1/2稀疏性约束，以及全变分的稀疏约束深度NMF[7]。与原始的NMF方法相比，改进的NMF方法得到了更好的结果。然而，当高光谱数据中存在噪声(即高斯噪声和条带)时，由于这些NMF方法中的最小二乘目标函数对噪声非常敏感，因此这些模型的性能会急剧下降[8,9,10]。为了降低噪声的影响，引入了鲁棒估计来取代传统的最小二乘度量，并提出了许多鲁棒NMF方法，如基于相关熵损失的鲁棒NMF (CENMF)[5]、基于ℓ2,1-范数和基于ℓ1,2-范数的NMF模型[11]。

本文采用鲁棒柯西损失函数(CLF)代替最小二乘损失，提出了一种高光谱解混的柯西NMF方法(CauchyNMF)。与传统的最小二乘损失相比，CLF的影响函数有一个上界。因此，它可以减轻单一元素的影响，特别是噪声较大的元素。在CauchyNMF的实现中，可以自动获得一个辅助向量来表示每个高光谱波段的重要性。对于噪声频带，CauchyNMF对应的权值相对较小，因此对噪声的鲁棒性较好。

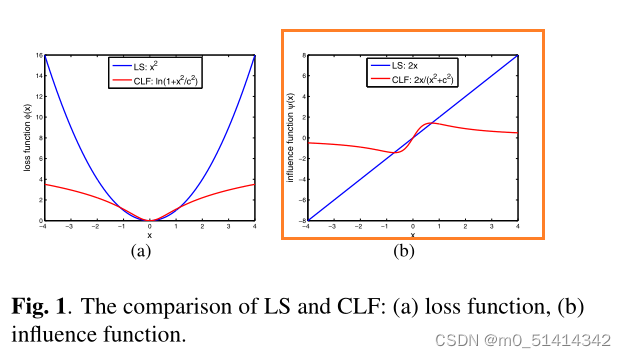
LS和CLF的损失函数和影响函数如图1所示。可以清楚地看到，CLF损耗可以抑制大噪声，其影响函数有上界，并随着误差的增大趋于零。 

 考虑到ℓ1/2-NMF解混模型(3)中的最小二乘损失函数对数据Y中的噪声或异常值敏感，我们引入柯西损失函数来替代模型(3)中的最小二乘损失，得到如下目标函数:

 

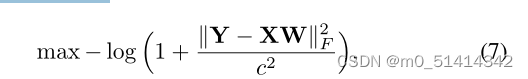
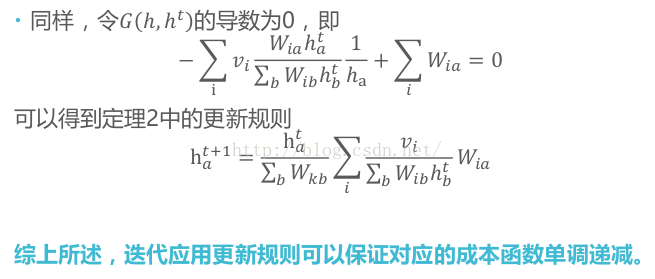
可以看出(7)中的目标函数是非凸的，是非线性的。因此，很难直接优化。这里，我们使用半二次型技术[14,8]来解决优化问题(7)，根据共轭函数的性质，我们有: