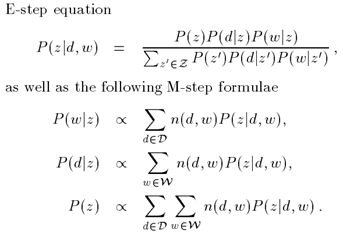<~生~信~交~流~与~合~作~请~关~注~公~众~号@生信探索>

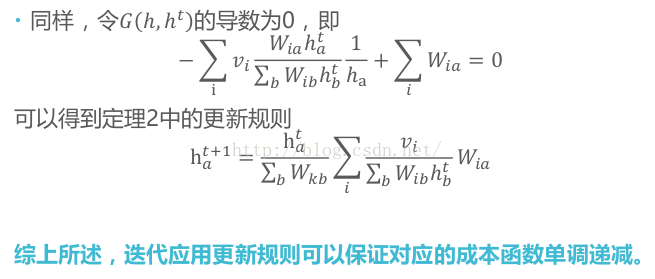
Non-Negative Matrix Factorization (NMF).

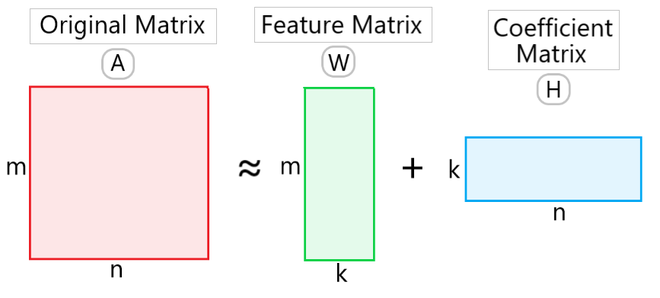
Find two non-negative matrices, i.e. matrices with all non-negative elements, (W, H) whose product approximates the non-negative matrix X. This factorization can be used for example for dimensionality reduction, source separation or topic extraction.

安装NMF

• ubuntu

ubuntu上，编译需要

sudo apt install libopenmpi-dev

• R

using(pak)
pak::pkg_install("NMF",dependencies=T)

使用

run_nmf(
    exp=exp,
    genelist=c("PCNA","HNRNPK","TRIM28","NPM1","PARK7","HDAC1")
) 

输入内容

• exp：表达矩阵，标准化过，但是不能有负数，行是基因，列是样本

#         TCGA-3L-AA1B-01A TCGA-4N-A93T-01A TCGA-4T-AA8H-01A
# MT-CO2          14.77639         15.77524         16.05650
# MT-CO3          15.13540         16.16666         15.84924
# MT-ND4          14.66976         14.80350         15.21889
# MT-CO1          13.98580         14.53619         15.30272
# MT-ATP6         13.53251         14.28397         14.60036

• genelist ：基因名向量，基因名需要在exp的行名中，如果为空则使用全部基因
• method: 最常用的三种brunet、lee、snmf/r
• n_run：运行次数

结果

结果怎么看https://mubu.com/doc/C4gVcgp-G0

R function

run_nmf <- function(
    exp,
    genelist=NULL,
    od = '.',
    n_cluster = 3,
    n_run=30,
    method="brunet",
    cluster_range=2:10,
    seed = 1314,
    cluster_character = "Cluster",

    ) 
{
    if (!dir.exists(od)) {
        dir.create(od)
    }

    if(!is.null(genelist)){
        exp <- exp[which(rownames(exp) %in% genelist), ]
    }
    
    using(NMF,data.table,tidyverse)

    if(is.numeric(cluster_range)){
        result <- NMF::nmf(exp,
            cluster_range,
            method = method,
            nrun = n_run,
            seed = seed
        )
        plot(result)
        ps(paste0(od, "/ranks.pdf"),w=10,h=10)
    }
    result2 <- NMF::nmf(exp, method = method, rank = n_cluster, seed = seed,nrun = n_run)
    key_gene <- NMF::extractFeatures(result2, 0.5) # 提取关键基因
    fwrite(data.table(key_gene=key_gene),paste0(od,'/key_gene.csv'))

    # 提出亚型
    Cluster <- as_tibble(predict(result2), rownames = "Sample") %>%
        dplyr::rename(Cluster = value) %>%
        dplyr::mutate(Cluster = paste0("Cluster", Cluster))
    fwrite(Cluster, paste0(od, "/NMF_Cluster.csv"))
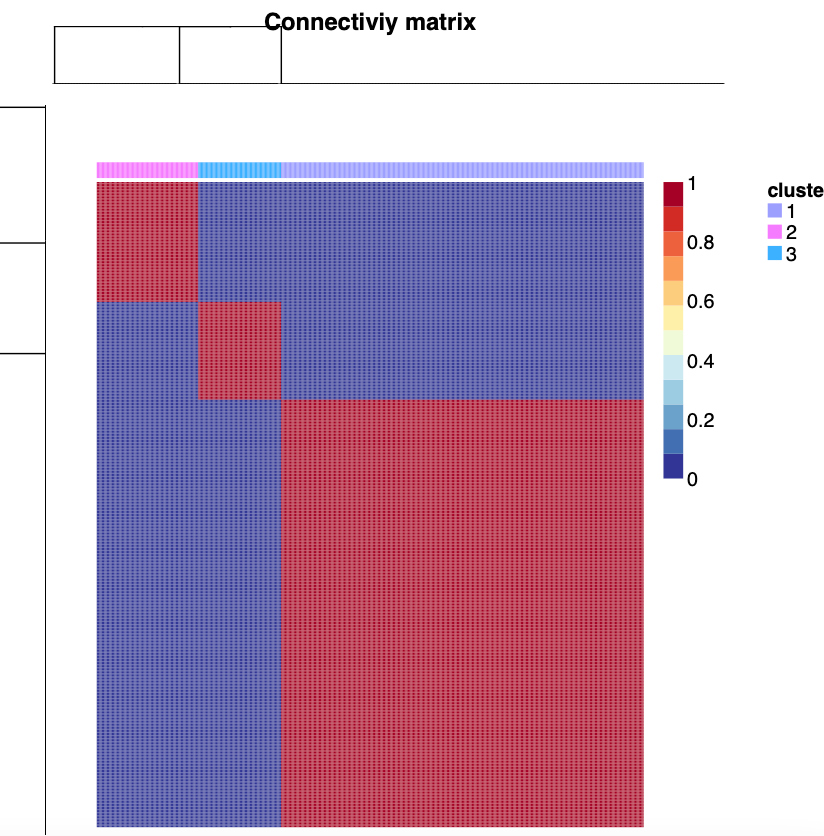
    consensusmap(result2,
        labRow = NA,
        labCol = NA,
        annCol = data.frame("cluster" = predict(result2)[colnames(exp)])
    )
    ps(paste0(od, "/Cluster.pdf"),w=6,h=6)
    return()
}
ps <- function(filename, plot = FALSE, w = 12, h = 6) {
    if (is.object(plot)) {
        print(plot)
    }
    plot <- recordPlot()
    pdf(file = filename, onefile = T, width = w, height = h)
    replayPlot(plot)
    dev.off()
}

Reference

https://cloud.tencent.com/developer/article/1806266
https://mubu.com/doc/C4gVcgp-G0
https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.NMF.html
https://www.geeksforgeeks.org/non-negative-matrix-factorization/