1. matlab示例解说

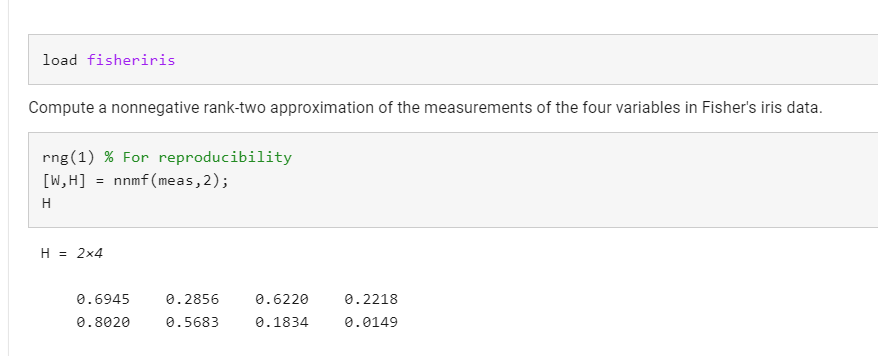
这一节的图片来自官方文档。

这里第一和第三变量在第一行的值0.6945和0.62220对W的第一列有相当强的权重。第一个第二变量在第二行的值0.8020和0.5683对W的第二列有相当大的权重。

官方文档2

其中，H的转置是4乘2大小的。也就是有4个变量【SW,SL,PL,PW】，2个特征【所以是二维坐标轴X和Y轴】，转化到二维图上。使用W当做’scores’做出散点图。然后标签是这四个。

2. NMF代码与Lenna图

这个函数是拷别人的，来自这里。

function [W,H,errs,loss] = nmf_euc(V, r)
% 输入检查
% 不含负值元素
% H为系数矩阵，一列不能全为0if min(min(V)) < 0error('Matrix entries can not be negative');
end
if min(sum(V,2)) == 0error('Not all entries in a row can be zero');
end% V是一个含有n个样本的矩阵，每一列对应一个样本，每个样本为m维
[m,n] = size(V);% 随机初始化W和H矩阵
W = rand(m,r);
H = rand(r,n);% 设置最大迭代次数，保证分解结果是收敛的
niter = 10000;myeps = 1e-10;errs = zeros(niter,1);for t = 1:niterW = W .* ( (V*H') ./ max(W*(H*H'), myeps) ); 
%   W = normalize_W(W,1);H = H .* ( (W'*V) ./ max((W'*W)*H, myeps) );loss = sum((V-W*H).^2);errs(t) = sum(sum(loss));
end

这一段是调用该函数与matlab自带的nnmf函数进行的实验。文件lenna图在后面，是一个彩图，真实大小是 $512\times 512\times 3$ 。所以使用了reshape函数。我知道lena是拼错的该是lenna，但懒得改。

clear 
clcV=double(imread('lena.jpg'));
imshow(mat2gray(V));V = reshape(V,512,1536);
[W,H] = nnmf(V,50);
img_V=W*H;
img_V = reshape(img_V,512,512,3);
figure;
imshow(mat2gray(img_V));V = reshape(V,512,1536);
[W,H,errs,loss] = nmf_euc(V, 100);img_V=W*H;
img_V = reshape(img_V,512,512,3);
figure;
imshow(mat2gray(img_V));

分解出来W大小是 $512\times 50$ ，H是 $50\times 1536$ 大小。分解之后再乘回去即可复原。可以发现matlab自带的nnmf函数复原结果不好。使用的Lenna图如下，直接保存就可以用了：

在这里插入图片描述
nnmf分解再复原

对不起，Lenna女士。然后是nmf_euc分解再复原的。这图边界那么大是因为我直接保存图片然后复制过来的，其实该复制图窗再处理，但是懒orz

可以发现比官方的要好很多。

3. NMF与人脸识别

使用的数据集来自这里的Yale database 32乘32的data file。使用下面的代码打乱顺序并储存

leng = size(gnd,1);
lis = randperm(leng);
gnd = gnd(lis,:);
fea = fea(lis,:);
save('yaleFace.mat','gnd','fea');

此后，对数据进行NMF分解

clear
clcload('yaleFace.mat')
fea = fea';
readFace = reshape(fea,32,32,165);
for i = 1:165imshow(readFace(:,:,i)./255)
endrng(1) % For reproducibility
k = 16;
[W,H] = nnmf(fea,k);
C = reshape(W,32,32,k);
for i = 1:kimshow(C(:,:,i)./255)
end

在这里对fea转置，所以实际上fea是1024乘165的。 $1024=32\times 32$ ，是维度。而165是样本数。在随机数种子rng(1)之前可以把原图给过一遍。此后，降维到k=16，那么W是 $1024\times 16$ 大小的基矩阵，H是 $16\times 165$ 的系数矩阵。

好了重点来了。我代码这么写的思路是：基矩阵就是平均脸，一共16张平均脸。16就是[W,H] = nnmf(fea,k);的k值。之后reshape成 $32\times 32$ 的16张平均脸脸图。系数矩阵H就是把这些平均脸加权的。如果把NMF的基矩阵看做坐标轴的话，系数矩阵就是使用这些坐标轴标记出来的点。所以下一步该进行的分类聚类等算法处理的是系数矩阵H。