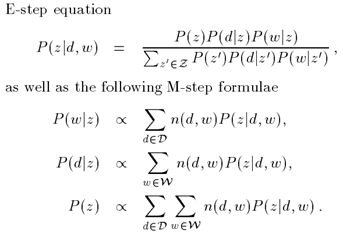NMF降维算法与聚类模型的综合运用

- 前言
- 一：NMF算法
- 二：NMF算法的使用
- 三：NMF算法与层次聚类的综合使用
- 四：总结

前言

这一章，我们讨论下另一个比较有效的降维手段：NMF（非负矩阵分解）。NMF降维理论的创建相比于经典的降维理论，略显“年轻”。我们接下来将详细介绍下NMF的原理以及在生产实践中的运算，结合代码和可视化图像来说明这些。

岁月如云，匪我思存，写作不易，望路过的朋友们点赞收藏加关注哈，在此表示感谢！

一：NMF算法

NMF又叫非负矩阵分解，为什么是“非负”？因为非负数据往往在实际中才是有意义的数据。 NMF本质上说是一种矩阵分解的方法，它的特点是可以将一个大的非负矩阵分解为两个小的非负矩阵，又因为分解后的矩阵也是非负的，所以也可以继续分解。因此，当我们数据集大小过于庞大时，NMF算法可以运用解决数据庞大而带来的复杂超额的计算量。

底层原理解释

1：简单概括

我们设数据 $D = m * n$ ，其中 $m$ 是数据的个数， $n$ 是数据特征。当矩阵 $D$ 非负时，我们令 $D_{(m∗n)}=W_{(m∗k)}∗H_{(k∗n) }$ （由代数知识知此解不会唯一，但每个解都是相应变换关系，含有的信息是相似的），其中 $k$ 为从矩阵 $D$ 中抽取的特征个数，则矩阵 $W$ 为包含 $k$ 个特征的基数据矩阵，也就是降维后的目标矩阵， $H$ 为对应的系数矩阵，
在这里插入图片描述

上图图1可以很形象的说明分解过程，其中s.t.意思为矩阵W、H的每个元素必须是>=0。

2：常见两种代价函数（损失函数）

矩阵 $W$ 和矩阵 $H$ 的求解也是近似解，为了寻找最优的 $W$ 和 $H$ ，我们要求欧式距离代价函数最小，即

$min‖D-D^′ ‖^2=min∑_{i,j}(D_{ij}-D_{ij}^′ )^2$ ，其中 $D^′=W∗H$

$K L$ 散度也是一种代价函数。 KL 简单一句话概括就是两个概率分布之间的差异性度量，在计算中，一个概率分布为真实分布，另一个为理论（拟合）分布， $K L$ 散度表示使用理论分布拟合真实分布时产生的信息损耗的期望值，我们用公式表示如下：
$D_{KL}(p||q)=E[log_2p(x)-log_2(q(x))]$ ，

那么对应的离散形式可以表示为：
$D_{KL}(p||q)=\sum_{i=1}^{N}{p(x_i)}(log_2p(x_i)-log_2q(x_i))$ ，

对应的连续形式可以表示为：
$D_{KL}(p||q)=\int_{-\infty}^{+\infty}p(x)(log_2p(x)-log_2q(x))dx$ ，

这里的 $p(x_i),q(x_i)$ 就是表示真实和理论上的每个随机变量的概率值。在进行NMF损失函数构建中，我们同样要求存在 $D^{'}$ 使得

$minD_{KL}(D||D^{'})=min\sum_{ij}\left[ {D_{ij}log_2\frac{D_{ij}}{D_{ij}^{'}}-D_{ij}+D_{ij}^{'}} \right]$ 存在。

3：参数的迭代优化

为保证矩阵的各个元素在非负状态下计算，针对上述两种代价函数，我们基于梯度下降方法设以下两种迭代公式（至于这两种迭代公式怎么来的，通过上述建立的损失函数再对各变量求偏导即可）

基于欧式距离的迭代公式：

$H_{\alpha j}^{k+1}=H_{\alpha j}^k\frac{\left( (W^k)^TD\right)_{\alpha j}}{\left( (W^k)^T(D^{'})^k\right)_{\alpha j}} 和 W_{i\alpha}^{k+1}=W_{i\alpha}^k\frac{\left( D(H^k)^T \right)_{i\alpha}}{\left( (D^{'})^k(H^k)^T\right)_{i\alpha}}$ ，

基于 $K L$ 散度迭代公式：

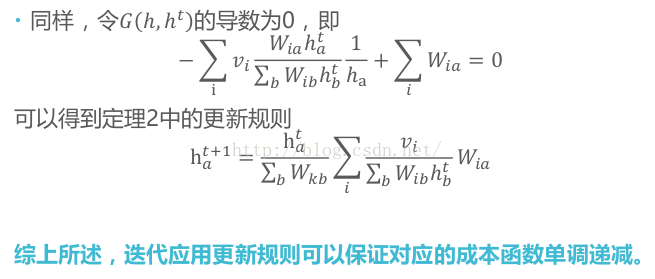
$H_{\alpha j}^{k+1}=H_{\alpha j}^k\frac{\sum_{i}{\left[ W_{i\alpha}^{k}D_{ij}/(D^{'})_{ij} \right]}}{\sum_{i}{W_{i\alpha}}}$ 和

$W_{i\alpha}^{k+1}=W_{i\alpha}^k\frac{\sum_{j}{\left[ H_{\alpha j}^{k}D_{ij}/(D^{'})_{ij} \right]}}{\sum_{j}{H_{\alpha j}}}。$

特别注意这里各个上标下标字母含义与计算过程。

在迭代过程中，我们设定好最大迭代次数或者代价函数的下界值为迭代终止条件。其中关于参数迭代能否收敛下去，有兴趣的朋友可以参考相关证明文献。以上就是整个NMF算法的底层原理介绍。

二：NMF算法的使用

NMF在实际降维中充当何种身份

在图像识别方面，NMF可以非常有效的压缩原始高维特征数据。为了更加形象描述NMF原理，我们举一个人脸例子。人脸包括“嘴巴、鼻子、眼睛、眉毛等等”，这时候我们只提取一些重要特征如“嘴巴、鼻子”等一些特殊信息，那么用这些独立部位信息的加权组合即可构成人的一张脸，公式 $H∗W=H∗[W_1,W_2,…W_n]$ 可以非常好的概括这一过程。而传统的PCA等只是对整个一张脸去除相似特征进行模糊处理而已。

在生物信息方面，由于NMF是分解不出来负数值的，所以对于生物上的数据，对于高蛋白质维度的数据降维，NMF是个很好的方法，可以很好的选择最有效的蛋白特征数据。

在语音识别方面，NMF算法成功实现了有效的语音特征提取，并且由于NMF算法的快速性，对实现机器的实时语音识别有着促进意义。

NMF的算法调用

我们直接调用函数，并参考官方文档给的参数解释如下

from sklearn.decomposition import NMF
nmf = NMF(n_components=2,init=None,  # W H 的初始化方法， 默认'nndsvd'，还有'random'，'nndsvda'，'nndsvdar'，'custom'.solver='cd',  # 'cd'，'mu'beta_loss='frobenius',  # 还有'kullback-leibler', 'itakura-saito'，此时的solver=‘mu’tol=1e-6,  # 停止迭代的误差下界值max_iter=500,  # 最大迭代次数random_state=None,alpha=0.,  # 正则化参数l1_ratio=0.,  # 正则化参数verbose=0,  # 冗长模式，类似于神经网络是否打印迭代过程shuffle=False  # 针对'cd solver')##常见函数打印如下：
print('params:', nmf.get_params())  # 获取构造函数参数的值nmf_model = NMF(n_components=4,verbose=1) #训练模型
W = nmf.fit_transform(X) #W矩阵
H = nmf.components_  # H矩阵
print('error_value', nmf.reconstruction_err_)  # 损失函数值
print('n_iter_', nmf.n_iter_)  # 实际迭代次数

三：NMF算法与层次聚类的综合使用

接下来，我们主要讨论NMF如何跟聚类算法综合使用来处理实际问题。NMF是一种有效降维手段，层次聚类是一种两空间点基于特定距离运算的自下而上的不断从小聚类簇合并成大聚类簇的聚类算法，算法理解比较直观，但运算量比较大。我们会结合层次系谱图和聚类热图来确定聚类数目和相应的聚类样本簇（这里有兴趣可以对比之前文章所介绍肘方法、CH值或者轮廓系数所确定的聚类数目）。可以参考本人之前的论文！

Heatmap中文称为热点图，热点图是通过使用不同的标志将图或页面上的区域按照受关注程度（分布数据大小）的不同加以标注并呈现的一种分析手段，标注的手段一般采用颜色的深浅、点的疏密以及呈现比重的形式。

实验代码编写

导入相关的模块和数据集信息，此次数据大小为（900,800）

from sklearn.decomposition import NMF
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pdplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falsedata = pd.read_csv(r'NMF与HC建模数据.csv',index_col=0,encoding='gbk')

NMF方法建立

d = 3##降维维度
nmf_model = NMF(n_components=d,random_state=11,alpha=2,solver='mu',beta_loss='kullback-leibler')##NMF方法相关参数
a_nmf = nmf_model.fit_transform(data_orginal)##W
b_nmf = nmf_model.components_##H

由于我们是根据系谱图和热图分布才能知晓聚成几类比较好，所以我们要先得到聚类后的重排序样本数据

根据重排序的样本数据和聚类数目，我们最终绘制热图

def makeheatmap(data,msg):_c = dict(zip(data.loc['cluster'].unique(), ['red', 'blue', 'orange']))_c_color = data.loc['cluster'].map(_c)heatmapdf = data.iloc[2:,:].astype(float)res_hm = sns.clustermap(heatmapdf,figsize=(15, 8),pivot_kws=None, method='average', metric='euclidean',dendrogram_ratio=0.1, colors_ratio=0.03,cbar_pos=(0.05, 0.1, 0.01, 0.5),tree_kws=None,# annot=True,  # 默认为False，当为True时，在每个格子写入data中数据# annot_kws={'size': 12, 'weight': 'normal', 'color': 'red'},# 设置格子中文本的大小、粗细、颜色cmap=sns.color_palette('RdBu_r', 21),##热图颜色row_cluster=False,  # 行方向不聚类col_cluster=True,  # 列方向聚类vmin=-1, vmax=1,col_colors=_c_color,# yticklabels = data.columns,# xticklabels = data.index,)legend_TN = [mpatches.Patch(color=c, label=l) for c, l in data.T[['color', 'cluster']].drop_duplicates().values]res_hm.ax_heatmap.legend(loc='center left', bbox_to_anchor=(1, 0.5), handles=legend_TN)plt.title(msg,fontsize=10)plt.show()
msg = '特征降至%s维后的热图分布'%d
makeheatmap(res_grdf,msg)

在这里插入图片描述

图1

从上图图1中，我们发现热图是存在明显的3块高表达区域，再结合层次系谱图，我们做出三种颜色的聚类线条。综上，在这些方法下，此数据聚成3类是比较合适。

四：总结

NMF结合相关聚类技术，是一种非常有效的综合聚类模型，当然，聚类方法很多（如之前我们底层编写的Kmean++），确定聚类数目方法很多（肘方法、轮廓系数、CH值等等），此文中的热图也是一种有效的确定聚类数目方法，更甚至降维技术也很多，如上篇的Kpca、Tsne等，都可以用于实际生产中解决问题
NMF的作用远远不仅于此，比如当我们涉及的数据大小过于庞大，直接把数据带入模型计算瞬间会消耗大量资源，但我们还要保持所有数据信息完整（不能进行特征提取或者降维处理），这时候我们也可以使用NMF算法，对庞大数据（数据先保证为非负）拆分然后根据矩阵运算规则进行切块计算，这样会避免瞬间过多消耗计算机资源。

在这里插入图片描述