写在篇前

  本篇文章主要介绍NMF算法原理以及使用sklearn中的封装方法实现该算法，最重要的是理解要NMF矩阵分解的实际意义，将其运用到自己的数据分析中！

理论概述

  NMF(Non-negative matrix factorization)，即对于任意给定的一个非负矩阵V，其能够寻找到一个非负矩阵W和一个非负矩阵H，满足条件V=W*H,从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。**其中，V矩阵中每一列代表一个观测(observation)，每一行代表一个特征(feature)；W矩阵称为基矩阵，H矩阵称为系数矩阵或权重矩阵。这时用系数矩阵H代替原始矩阵，就可以实现对原始矩阵进行降维，得到数据特征的降维矩阵，从而减少存储空间。**过程如下图所示：

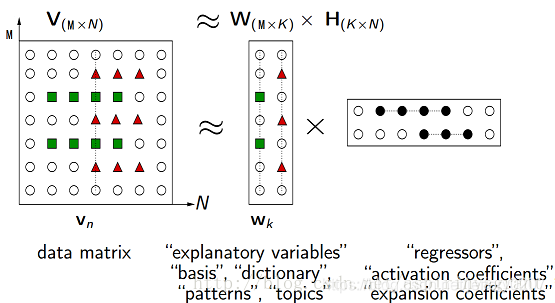
  nmf更详尽的原理可以参考Non-negative matrix factorization - Wikipedia，这里我主要列出我很关注的损失函数(lossFunction or objective function)：

• squared frobenius norm
  $$\underset{W,H}{\underbrace{argmin}}\frac{1}{2}||A-WH|{|}_{Fro}^2+\alpha \rho ||W|{|}_1+\alpha \rho ||H|{|}_1+\frac{\alpha (1-\rho )}{2}||W|{|}_{Fro}^2+\frac{\alpha (1-\rho )}{2}||H|{|}_{Fro}^2$$
  ​ 其中：
  $$\frac{1}{2}||A-WH|{|}_{\mathrm{F}\mathrm{r}\mathrm{o}}^2=\frac{1}{2}\sum _{i,j}(A_{ij}-{WH}_{ij}{)}^2$$
  ​ $\alpha$为L1&L2正则化参数，而\rho为L1正则化占总正则化项的比例。||*||_1为L1范数。

• Kullback-Leibler (KL)
  $$d_{KL}(X,Y)=\sum _{i,j}(X_{ij}\log (\frac{X_{ij}}{Y_{ij}})-X_{ij}+Y_{ij})$$

• Itakura-Saito (IS)

$$d_{IS}(X,Y)=\sum _{i,j}(\frac{X_{ij}}{Y_{ij}}-\log (\frac{X_{ij}}{Y_{ij}})-1)$$
​ 实际上，上面三个公式是beta-divergence family中的三个特殊情况（分别是当$\beta =2,1,0$），其原型是：
$$d_{\beta }(X,Y)=\sum _{i,j}\frac{1}{\beta (\beta -1)}(X_{ij}^{\beta }+(\beta -1)Y_{ij}^{\beta }-\beta X_{ij}{Y}_{ij}^{\beta -1})$$

代码实现

代码解读

   在sklearn封装了NMF的实现，可以非常方便我们的使用，其实现基本和前面理论部分的实现是一致的，但是注意sklearn中输入数据的格式是（samples, features）：

from sklearn.decomposition import NMF
from sklearn.datasets import load_irisX, _ = load_iris(True)# can be used for example for dimensionality reduction, source separation or topic extraction
# 个人认为最重要的参数是n_components、alpha、l1_ratio、solver
nmf = NMF(n_components=2,  # k value,默认会保留全部特征init=None,  # W H 的初始化方法，包括'random' | 'nndsvd'(默认) |  'nndsvda' | 'nndsvdar' | 'custom'.solver='cd',  # 'cd' | 'mu'beta_loss='frobenius',  # {'frobenius', 'kullback-leibler', 'itakura-saito'}，一般默认就好tol=1e-4,  # 停止迭代的极限条件max_iter=200,  # 最大迭代次数random_state=None,alpha=0.,  # 正则化参数l1_ratio=0.,  # 正则化参数verbose=0,  # 冗长模式shuffle=False  # 针对"cd solver")# -----------------函数------------------------
print('params:', nmf.get_params())  # 获取构造函数参数的值，也可以nmf.attr得到，所以下面我会省略这些属性# 下面四个函数很简单，也最核心，例子中见
nmf.fit(X)
W = nmf.fit_transform(X)
W = nmf.transform(X)
nmf.inverse_transform(W)
# -----------------属性------------------------
H = nmf.components_  # H矩阵
print('reconstruction_err_', nmf.reconstruction_err_)  # 损失函数值
print('n_iter_', nmf.n_iter_)  # 实际迭代次数

注意点：

• init参数中，nndsvd（默认）更适用于sparse factorization，其变体则适用于dense factorization.
• solver参数中，如果初始化中产生很多零值，Multiplicative Update (mu) 不能很好更新。所以mu一般不和nndsvd使用，而和其变体nndsvda、nndsvdar使用。
• solver参数中，cd只能优化Frobenius norm函数；而mu可以更新所有损失函数

案例1

  第一个案例很简单，目的是理解分解出来的这两个矩阵能用来干嘛，分别是什么意思，但是其实我在文章第一部分已经解释了，直接看例子：

>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import NMF
>>> model = NMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
>>> X_new = np.array([[1, 0], [1, 6.1], [1, 0], [1, 4], [3.2, 1], [0, 4]])
>>> W_new = model.transform(X_new)
>>> W_new  # 输出 W_new

array([[0.35919303],
​ [0.86264547],
​ [0.35919303],
​ [0.68932578],
​ [1.23195088],
​ [0.33013275]])

  ok，这个小例子就说明了我们通过NMF获得系数矩阵H,并用系数矩阵H获得新矩阵W_new的基矩阵，实现W_new的数据降维(or 特征提取)。实际上，这时W_new = model.transform(X_new)做的工作相当于：

np.mat(X_new)*(np.mat(H).I)

matrix([[0.35919303],
​ [0.86264547],
​ [0.35919303],
​ [0.68932578],
​ [1.23195088],
​ [0.33013275]])

案例2

  这里再举一个NMF在图像特征提取的应用，来自官方示例，根据我的需要改动了一些：

from time import time
from numpy.random import RandomState
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_olivetti_faces
from sklearn import decompositionn_row, n_col = 2, 3
n_components = n_row * n_col
image_shape = (64, 64)
rng = RandomState(0)# #############################################################################
# Load faces data
dataset = fetch_olivetti_faces('./', True,random_state=rng)
faces = dataset.datan_samples, n_features = faces.shapeprint("Dataset consists of %d faces, features is %s" % (n_samples, n_features))def plot_gallery(title, images, n_col=n_col, n_row=n_row, cmap=plt.cm.gray):plt.figure(figsize=(2. * n_col, 2.26 * n_row))plt.suptitle(title, size=16)for i, comp in enumerate(images):plt.subplot(n_row, n_col, i + 1)vmax = max(comp.max(), -comp.min())plt.imshow(comp.reshape(image_shape), cmap=cmap,interpolation='nearest',vmin=-vmax, vmax=vmax)plt.xticks(())plt.yticks(())plt.subplots_adjust(0.01, 0.05, 0.99, 0.93, 0.04, 0.)# #############################################################################
estimators = [('Non-negative components - NMF',decomposition.NMF(n_components=n_components, init='nndsvda', tol=5e-3))
]# #############################################################################
# Plot a sample of the input dataplot_gallery("First centered Olivetti faces", faces[:n_components])# #############################################################################
# Do the estimation and plot itfor name, estimator in estimators:print("Extracting the top %d %s..." % (n_components, name))t0 = time()data = facesestimator.fit(data)train_time = (time() - t0)print("done in %0.3fs" % train_time)components_ = estimator.components_print('components_:', components_.shape, '\n**\n', components_)plot_gallery('%s - Train time %.1fs' % (name, train_time),components_)
plt.show()#---------------------------其他注释---------------------------
V矩阵：400*4096
W矩阵：400*6
H矩阵：6*4096

  下面是script运行结果：

写在篇后

  NMF最早由科学家D.D.Lee和H.S.Seung提出的一种非负矩阵分解方法，并在Nature发表文章《Learning the parts of objects by non-negative matrix factorization》。随后也有了很多NMF变体，应用也越发广泛，包括文本降维、话题提取、图像处理等。这里必须指出，我看到一份NMF非常完整的资料，但是精力有限，不能全面cover，有兴趣的同学可以参考nimfa。