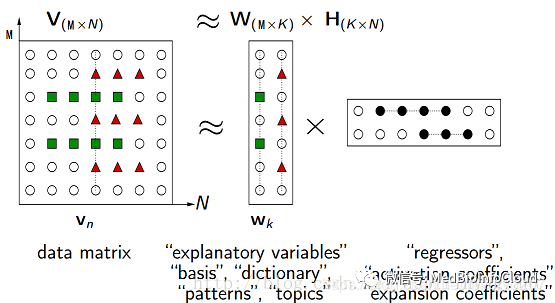
NMF(Non-negative matrix factorization，非负矩阵分解)，即对于任意给定的一个非负矩阵V，其能够寻找到一个非负矩阵W和一个非负矩阵H，满足条件V=W*H,从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。其中，V矩阵中每一列代表一个观测(observation)，每一行代表一个特征(feature)，比如RNAseq的样本(列)和基因(行)的表达矩阵；W矩阵称为基矩阵，H矩阵称为系数矩阵或权重矩阵。这时用系数矩阵H代替原始矩阵，就可以实现对原始矩阵进行降维，得到数据特征的降维矩阵，从而减少存储空间。过程如下图所示：

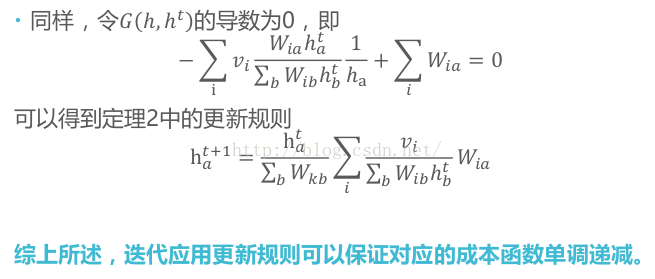
下面用数学语言对NMF进行描述，并直接给出求解NMF的迭代公式。

NMF的本质是通过一个矩阵去求解两个为止矩阵。上图采用的是迭代法，一步步逼近最终的结果，当计算得到的两个矩阵W和H收敛时，就说明分解成功。需要注意的是，原矩阵和分解之后两个矩阵的乘积并不要求完全相等，可以存在一定程度上的误差。

如果要在计算机中实现NMF，则可以根据下图所示的步骤进行。

nmf更详尽的原理可以参考维基百科：Non-negative matrix factorization。

NMF的计算机实现可以用python、Java和R，作为生信专业的我们，用python和R估计会多一些，我后面会介绍怎么用R实现NMF。

本文参考文章:

【2】https://blog.csdn.net/ctyqy2015301200079/article/details/86725427