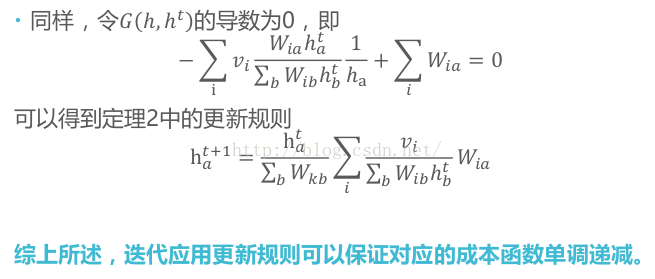
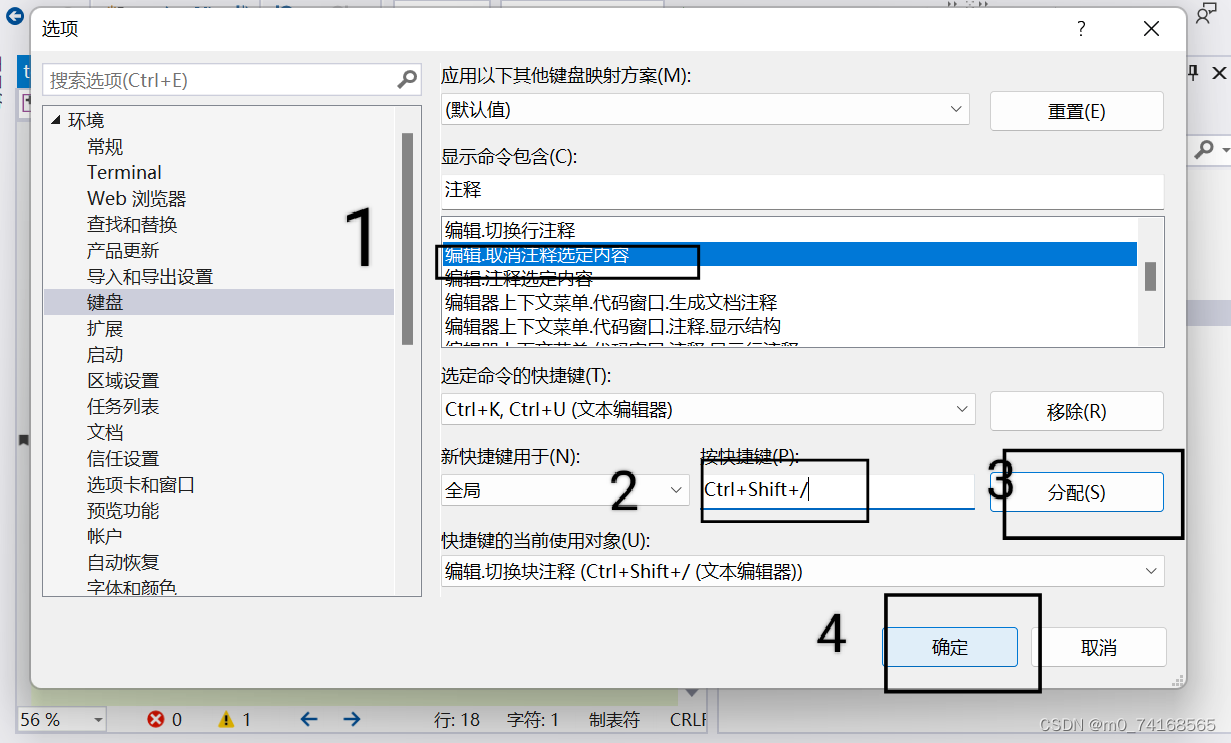
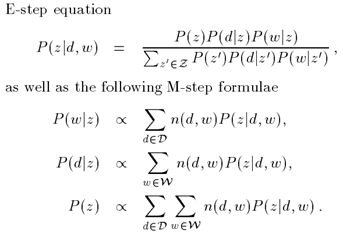ADMM求解优化NMF

article/2025/9/21 12:57:53

本文拟对文章：“An Alternating Direction Algorithm for Matrix Completion with Nonnegative Factors”中利用ADMM进行非负矩阵分解部分进行推导。

$min_{U,V}\|X-WH\|_2^2;\\ s.t\quad W,H\geq 0$

他的 augmented Lagrangian 可写成如下形式：

${{\cal L}_A}(X,{\rm{W}},H,Hp,Wp,\tilde H,\tilde W) = \frac{1}{2}\|X - WH\|_F^2 + \tilde W \bullet (W - Wp) + \tilde H \bullet (H - Hp) + \frac{\rho }{2}\|W - Wp\|_F^2 + \frac{\rho }{2}\|H - Hp\|_F^2$ (1)
(1)优化W

$\frac{{\partial L}}{{\partial W}} = - X{{\rm{H}}^T} + WH{H^T} + \tilde W + \rho \left( {W - Wp} \right) = 0;W\left( {H{H^T} + \rho I} \right) = X{{\rm{H}}^T} + \rho Wp - \tilde W,W = \left( {X{{\rm{H}}^T} + \rho Wp - \tilde W} \right){\left( {H{H^T} + \rho I} \right)^{ - 1}}$

(2)优化H:

$\frac{{\partial L}}{{\partial H}} = - {W^T}X + {W^T}WH + \tilde H + \rho \left( {H - Hp} \right) = 0;\left( {{W^T}W + \rho I} \right)H = {W^T}X - \tilde H + \rho Hp;H = {\left( {{W^T}W + \rho I} \right)^{ - 1}}\left( {{W^T}X - \tilde H + \rho Hp} \right).$

（3）优化Wp,Hp:

$\begin{array}{*{20}{l}} {\frac{{\partial L}}{{\partial Hp}} = - \tilde H - \rho \left( {H - Hp} \right) = 0;Hp = \max \left( {H + \rho \tilde H,0} \right)}\\ {\frac{{\partial L}}{{\partial Wp}} = - \tilde W - \rho \left( {W - Wp} \right) = 0;Wp = \max \left( {W + \rho \tilde W,0} \right)} \end{array}$

(4)优化 $\widetilde{W},\widetilde{H}$ :

$\begin{array}{l} \tilde H = \tilde H + \gamma \rho {\left( {H - Hp} \right)^T}\\ \tilde W = \tilde W + \gamma \rho {\left( {W - Wp} \right)^T} \end{array}$

迭代终止条件：

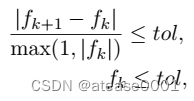
orl人脸库（32*32）上，目标函数收敛曲线：

聚类结果比较：

略好于传统NMF优化方法基于原始数据的聚类结果。

matlab代码：

function [W, H] = nmf_admm(V, W, H)
% nmf_admm(V, W, H)%
% inputs
%    V: matrix to factor 
%    W, H: initializations for W and H
%
% outputs
%    W, H: factorization such that V \approx W*H% determine dimensions[m,n] = size(V);[~,k] = size(W);rho = 1;gamma = 0.01;% initializations for other variablesX = V';Wplus = W;Hplus = H;alphaW = zeros(size(W));alphaH = zeros(size(H));maxiter = 10000;for iter=1:maxiter% update for WP = H*H' + rho*eye(k);Q = X*H' + rho*Wplus - alphaW;W = ( P'\ Q' )';% update for HH = (W'*W + rho*eye(k)) \ (W'*X- alphaH + rho*Hplus);% update for H_+ and W_+Hplus = max((H + 1/rho*(alphaH)), 0);Wplus = max(W + 1/rho*alphaW, 0);% update for dual variablesalphaH = alphaH + gamma*rho*(H - Hplus);alphaW = alphaW + gamma*rho*(W - Wplus);temp1 = 0.5*trace((X-W*H)'*(X-W*H));temp2 = trace(alphaW'*(W-Wplus)) + trace(alphaH'*(H-Hplus));temp3 = 0.5*rho*(trace((Wplus - W)*(Wplus - W)')+trace((Hplus - H)*(Hplus - H)'));fk = temp1 + temp2 + temp3;fk0 = fk/trace(X*X').^0.5;if iter>1err(iter-1) = fk;if abs(fk0-fk1)/max(1,abs(fk))<1e-6 break;endendfk1=fk0;
%         alphaW1 = alphaW;
%         alphaH1 = alphaH;endW = Wplus;H = Hplus; end