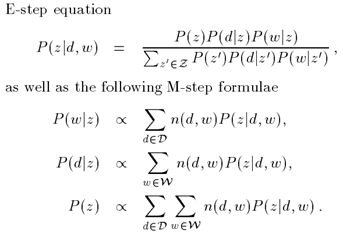NMF简介

NMF也是一种降维方法，相比PCA具有以下特点：

1，可解释性

2，可以用于所有数据集类型（PCA不能用于csr_matrix类型）

3，要求样本特征必须非负，像是表示每日股票价格升降的数组就不可以

NMF用于文本降维

现在我们将NMF用在类型为csr_matrix的wiki_features上，先print一下看看它的内容：

<script.py> output:wiki_features.shape is  (60, 13125)wiki_features is  (0, 16)  0.024688249778400003(0, 32)	0.0239370711117(0, 33)	0.0210896267411:	:(59, 13107)	0.025819936285200004(59, 13108)	0.0340972474957(59, 13113)	0.0170000449408wiki_features.toarray() is  [[0.         0.         0.         ... 0.         0.         0.        ][0.         0.         0.02960744 ... 0.         0.         0.        ][0.         0.         0.         ... 0.01159441 0.         0.        ]...[0.         0.         0.         ... 0.         0.         0.        ][0.         0.00610985 0.         ... 0.         0.00547551 0.        ][0.         0.         0.         ... 0.         0.         0.        ]]

其中通过.shape可以看出原始数据有60篇文章，13125种字。.toarray()中第 i 个横向量表示第 i 篇文章中这13125种字的 "tf-idf" 值。其中，"tf" 表示每种字在第 i 篇文章中出现的频率，可以通过这种字出现的次数除以第 i 篇文章总字数计算；"idf" 是一种加权方法，可以减少频词的作用，比如冠词 "the" 。

现在我们来使用NMF给wiki_features降下维叭

# 导入相应的库
from sklearn.decomposition import NMF# 创建一个model，注意NMF必须规定降到的维数 n_components ，但是PCA不必要
model = NMF(n_components = 6)# 训练模型
model.fit(wiki_features)# 降维
nmf_features = model.transform(wiki_features)# 输出维度与内容
print(nmf_features.shape)
print(nmf_features.round(2))

最后输出结果如下，我们可以看到13125变成了6，内容的输出咱们保留了两位小数。

<script.py> output:(60, 6)[[0.   0.   0.   0.   0.   0.44][0.   0.   0.   0.   0.   0.57][0.   0.   0.   0.   0.   0.4 ]:              :              ::              :              :[0.45 0.   0.   0.   0.01 0.  ][0.29 0.01 0.01 0.01 0.19 0.01][0.38 0.01 0.   0.1  0.01 0.  ]]

NMF的可解释性

那么这个结果是怎么得到的呢？其实是wiki_features (60, 13125) 与 model.components_转置 (13125, 6)的乘积，我们可以来验证一下~


<script.py> output:model.components_.shape is (6, 13125)(np.mat(wiki_features)*(np.mat(model.components_).I)).round(2) is  [[-0.01 -0.01 -0.   -0.02 -0.    0.44][-0.   -0.   -0.   -0.   -0.01  0.57][ 0.    0.   -0.01 -0.01 -0.    0.4 ]:                 :                 ::                 :                 :     [ 0.45 -0.   -0.   -0.02  0.01 -0.01][ 0.29  0.01  0.01  0.01  0.19  0.01][ 0.38  0.01 -0.    0.1   0.01 -0.  ]]

所以我们说NMF具有可解释性，每篇文章降维后的nmf.features是通过清晰的公式计算得到的。

咱们还可以用DataFrame格式看每篇文章降维后的特征向量，

# 导入pandas库
import pandas as pd# 创建DataFrames，用标题进行索引
df = pd.DataFrame(nmf_features,index = titles)# 输出'Anne Hathaway'文章的components
print(df.loc['Anne Hathaway'])

输出的结果如下：

<script.py> output:0    0.0038451    0.0000002    0.0000003    0.5757114    0.0000005    0.000000Name: Anne Hathaway, dtype: float64

NMF用于归纳单篇文章主题

除了降维以外，我们还可以用NMF做很多工作，比如利用 model.components_ 归纳文章主题。比如《Anne Hathaway》在 nmf.features 保存的数据中第 3 行( 0.575711 )远大于其他几行，所以我们可以查看一下 model.components_ 的第 3 个component是什么，从而推出这篇文章的主题。

# 先创建一个方便索引model.components的表格
# 导入 pandas 库
import pandas as pd# 创建表格，model.components是(6, 13125) 的数组，很容易知道它的每一列都表示一种字
components_df = pd.DataFrame(model.components_,columns=words)# 输出看看
print(components_df)

<script.py> output:aaron     abandon    abandoned ... zone      zones     zoo0  0.011375  0.001210   0.000000  ... 0.000000  0.000424  0.01  0.000000  0.000010   0.005663  ... 0.002813  0.000297  0.02  0.000000  0.000008   0.000000  ... 0.000000  0.000143  0.03  0.004148  0.000000   0.003056  ... 0.001742  0.006720  0.04  0.000000  0.000568   0.004918  ... 0.000192  0.001351  0.05  0.000139  0.000000   0.008748  ... 0.002401  0.001682  0.0[6 rows x 13125 columns]

索引到第 3 个componets，但是我们知道一行components有13125种字，不可能全是主题，所以我们使用 .nlargest() 前五个最大值对应的字。

# 选择第三行（注意是从0开始编号）
component = components_df.iloc[3]# 输出最大的五个值对应的文字
print(component.nlargest())

最后输出的结果：

<script.py> output:film       0.627877award      0.253131starred    0.245284role       0.211451actress    0.186398Name: 3, dtype: float64

NMF用于推荐多篇相似文章

其实可以再进一步，使用 nmf_features 找出与这篇文章主题类似的其他文章，类似浏览器中的推荐功能。

直接比较 nmf_features 是不合理的，因为同一主题的文章对应的的 nmf_features 不一定相似。因为有些文章的主题表达的比较直接，有些比较隐晦（废话多），后者的主题词频可能被稀释。所以我们选择余弦相似度来比较，因为将这些同一主题的文章对应的 nmf_features 画成散点图，虽然绝对值不同，但是都近似在一条过原点的直线上，这样通过比较直线就可以比较文章主题。

下面我们来看具体的代码叭。

# 导入Pandas库
# 为了计算方便，用点积代表余弦值，可以将每一行数组化成单位向量再输入，这里调用了normalize
import pandas as pd
from sklearn.preprocessing import normalize# 矢量归一化
norm_features = normalize(nmf_features)# 创建一个表格
df = pd.DataFrame(norm_features, index = titles)# 选定一篇文章
target_article = df.loc['Anne Hathaway']# 计算这篇文章与其他文章的余弦相似度，即归一化后的点积
similarities = df.dot(target_article)# 选择相似度最大的前五篇文章
print(similarities.nlargest())

最后输出结果：

<script.py> output:Anne Hathaway           1.000000Michael Fassbender      0.999978Catherine Zeta-Jones    0.999978Jessica Biel            0.999978Mila Kunis              0.999900dtype: float64