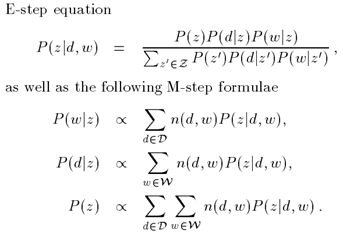题目:Multi-view clustering by non-negative matrix factorization with co-orthogonal constraints
一、创新点
和其他使用NMF的方法一样,这篇文章也是加约束,使创造出来的representation matrices更好。这篇文章加的约束叫做co-orthogonal constraints(联合正交约束)。
二、论文的思想
这篇文章的前置文章是Diverse Nonnegative Matrix Factorization for Multi-view Data Representation。这里大概说一下这篇前置文章的思路。
里面有一张图画得很好:

这里的多视图融合策略采用了将表征矩阵直接平均相加的方法。再用k-means等单视图聚类算法对H*进行聚类。这就要求:
- 每个视图的表征矩阵形状一样
- 各个视图在进行表征的时候,就应该有所交流。
这篇文章着重注意了视图之间的diversity,也就是差异性。以前的表征方法,每个视图只管自己,在H1出现过的表征信息有可能又会在H2中再次出现,这就造成了信息冗余。按照常理,H1挖过的信息,H2不应该再挖,没有意义。所以,应该保证H(1)和H(2)的对应列有差异。如图中,Existing approaches中间的那两个绿色矩阵的最后一列,特征分布是差不多的,但是在DiNMF中就错开了。这种让矩阵对应地方错开的数学方法,叫做正交。
明白了这个思想,我们再来看NMF-CC算法。
三、目标函数的构建
这个算法的目标函数很长,用了整整五个项,四个约束项,每个约束都代表了不同的思路。我们一个一个来看。

1.第一项
这项没什么好说的,就是标准的NMF。X是原数据矩阵,V是representation matric。剩下的几项都是为了让V的效果更好。
2.第二项
两个矩阵相乘以后秩的总和,其实就是把两个矩阵对应的每一个元素相乘,然后再把乘积加起来。将这个“和”最小化可以让两个矩阵错开,对应元素一个有值,一个为0.
而这里的矩阵是两个视图的representation,最小化他们乘积的秩可以让两个视图之间挖取的信息有差异。
3.第三项
原数据X=UV。我们一般用V代表representation。但既然原数据是两个矩阵相乘得来的,那么U其实也是包含了信息的,是可以利用的。怎么利用呢?作者说根据参考文献【28,31】证明,如果U的列向量之间越独立,那么V的表征效果就越好。为什么?比如, X 11 X_{11} X11是由U的第一行和V的第一列点乘得到。如果U的列向量之间越独立,U的第一行的元素会越正交,V的第一列有用的元素会越少。U的列相互独立,就是要最小化![]() 写成矩阵形式:
写成矩阵形式:![]()
括号中的第一项是指U中每一列都和其他列算一个向量的乘法,包括自己。因为多算了自己和自己的乘法,所以要减掉,也就是第二项。因为某一项和另一项算乘法之后,另一项也会和某一项再算一遍,所以就多算了一次,要乘1/2。
4.第四项
作者没有给任何的过程,但在其他论文里边已经应用过了。我把MvDGNMF里边的过程贴到这这边。


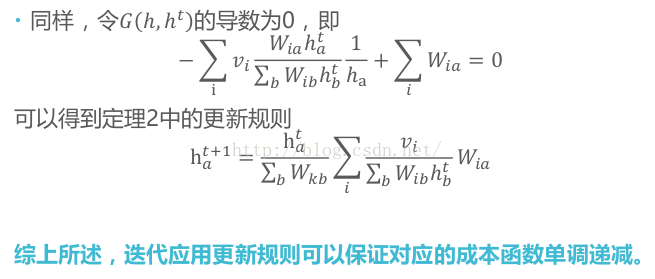
H是representation,D-W是一个拉普拉斯矩阵。这里的W采用的是0–1 weighting strategy。如果i点属于j点的第q个邻居之内,那么Wij就为1,否则为0。注意,这里的W算的是原始点X。

从下往上倒推,第一排公式的意思是,距离更近的X所转化为的H应该更相似。
5.第五项
V同自己转秩的乘积矩阵靠近单位矩阵I,意味着,V中的每一个行向量都会尽量和其他行向量的对应的元素错开。

如图V1和V2种,每一列都只有一个小黑点。这样可以让每一个X的表征都尽量用更少的特征进行表示,更大程度地减少了冗余信息,只留下最重要的,让表征更干净,更简洁。