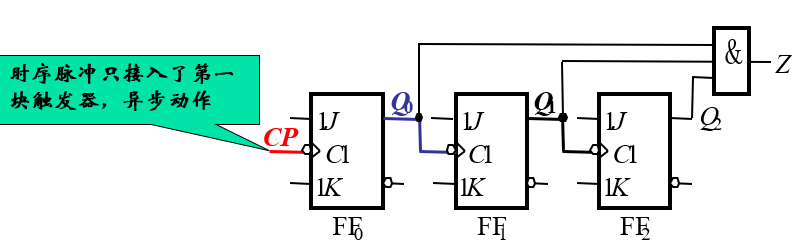
同步时序逻辑电路的设计,就是根据逻辑问题的具体要求,结合同步时序逻辑电路的特点,设计出能够实现该逻辑功能的最简同步时序电路。
同步时序逻辑电路中含有组合逻辑电路部分和存储电路部分,组合电路的设计在之前已作介绍.本节主要介绍存储电路部分的设计。存储电路部分主要用到的是触发器。
设计方法
同步时序逻辑电路的设计的过程表示如下:

需求分析
根据电路的设计要求,确定输入量和输出量,并且定义输入和输出量逻辑值的含义,用字母表示出这些变量,例如输入量用X表示,输出量用Y或Z等表示。
确定状态
根据设计要求,确定系统的原始状态数,用字母表示出这些原始状态,例如用Sm来表示(m为0、1、2…)。找到原始状态Sm之间的转换关系,作出在各种输入条件下状态间的转换图或状态转移表,标明输入和输出的逻辑值。
状态化简
在建立原始状态数时,主要是反映逻辑电路设计的要求,定义的原始状态图可能比较复杂,含有的状态数也较多,也可能包含了一些重复的状态。在设计中是要用最少的逻辑器件达到设计要求,如果逻辑状态较多,相应用到的触发器也就多,设计的电路就较复杂。为此,应该对原始状态进行化简,消去多余的状态,从而得到最简化的状态转换图。
状态的化简就是进行状态合并。用一个状态代替与之等价的状态。逻辑状态等价的依据是:
1. 状态Si、Sj,在相同的输入条件下,状态Si、Sj对应的输出结果相同;
2. 状态Si、Sj,在相同的输入条件下,状态Si、Sj转移效果完全相同。
满足上述两个条件的状态,就是等价状态,可以将这些等价状态合并为一个状态。
状态Si、Sj转移效果相同的情况可能有以下三种情况:
(相同输入/输出组对应的)次态相同
状态Si、Sj,在所有相同的输入条件下,转移到相同的次态,则状态Si、Sj转移效果相同,可以进行状态合并。下图说明了两个状态在相同的输入条件下次态相同的情况,用[Si ,Sj]来表示状态Si、Sj的等价,称为一个等价类,Si和Sj可以合并为一个状态。
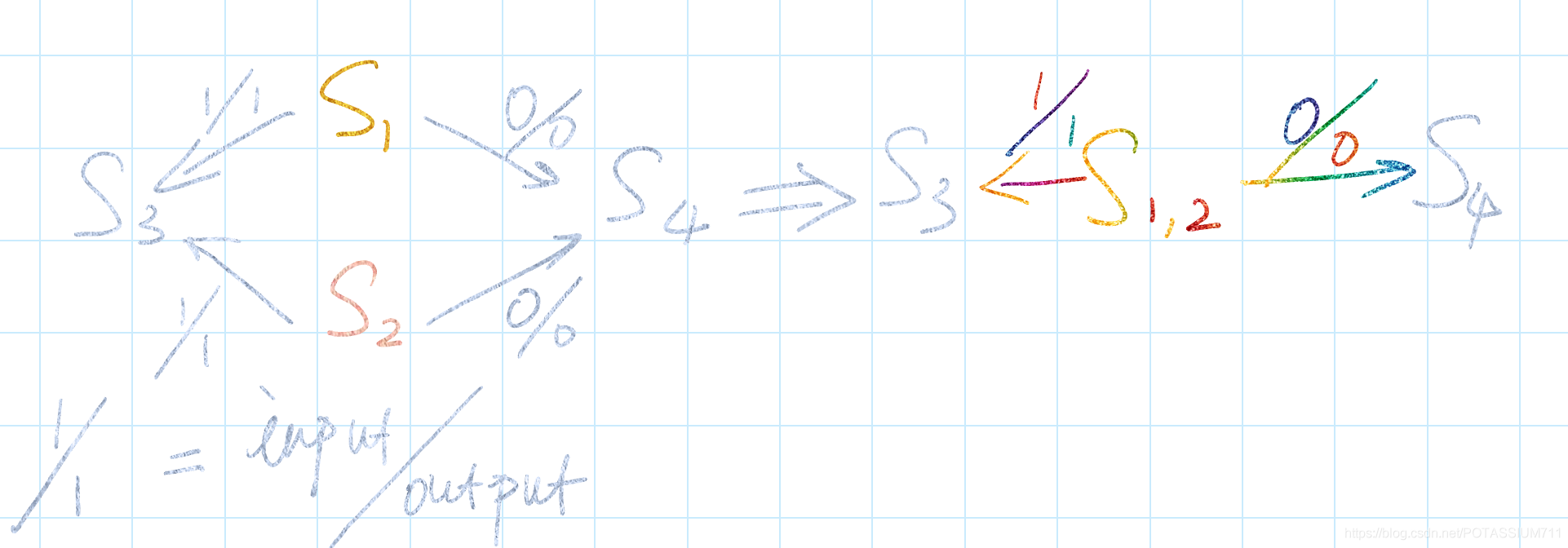
等价关系的传递性
等价关系具有传递性.如图所示,S1、S3在相同的输入条件下分别转移到S2和S4状态,它们的输出也相同,而S2和S4在相同的输入条件下转移到相同的次态S5,输出也相同,S2和S4是等价状态,所以S1和S3也是等价的,可以合并。用[S1,S3]来表示状态S1、S3的等价,S1和S3是一个等价类。用[S2,S4]来表示状态S2、S4的等价,S2和S4是一个等价类。
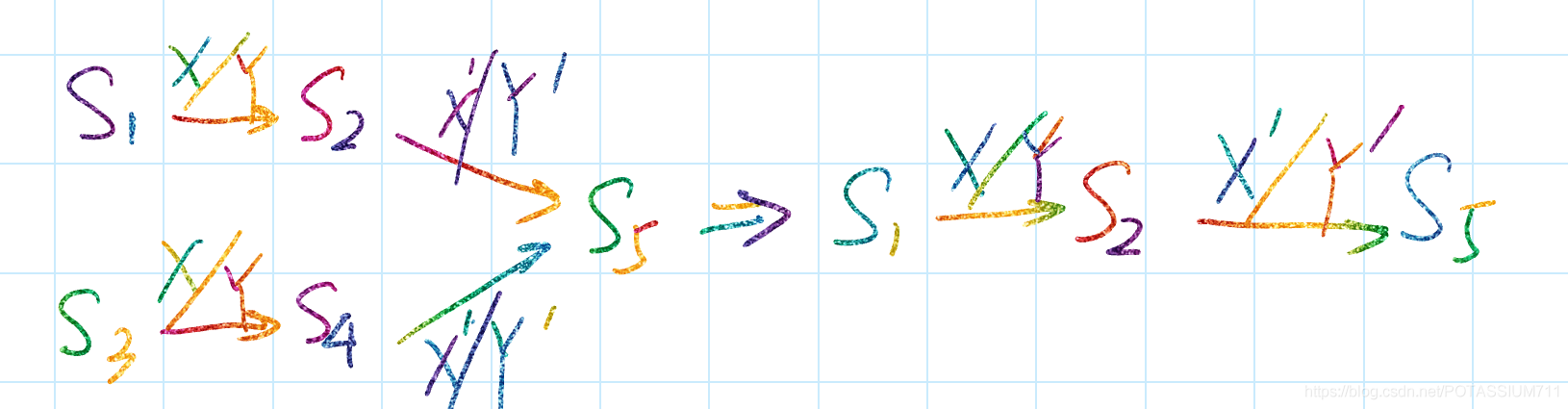
对于逻辑状态较多或者不能直接看出逻辑间的等价时,可以用隐含表法来寻找状态的等价.
这一种主要用在两两等效对检查完毕之后的最大等效类的判断.在最开始的检定过程中还是以其他三种为主.
次态交错
次态循环是指次态之间的关系构成循环。**并在另一组输入下次态和输出均相同.**如Si和Sj在某种输入条件下的次态分别为Sm和Sn,并且输出相同;Sm和Sn在另外输入条件下的次态分别为Si和Sj,输出也相同,则状态Si和Sj等价,用[Si ,Sj]来表示状态等价。

次态循环
次态循环是指次态之间的关系构成循环。如Si和Sj在某种输入条件下的次态分别为Sm和Sn,并且输出相同;Sm和Sn在另外输入条件下的次态分别为Si和Sj,输出也相同,则状态Si和Sj等价,用[Si ,Sj]来表示状态等价。
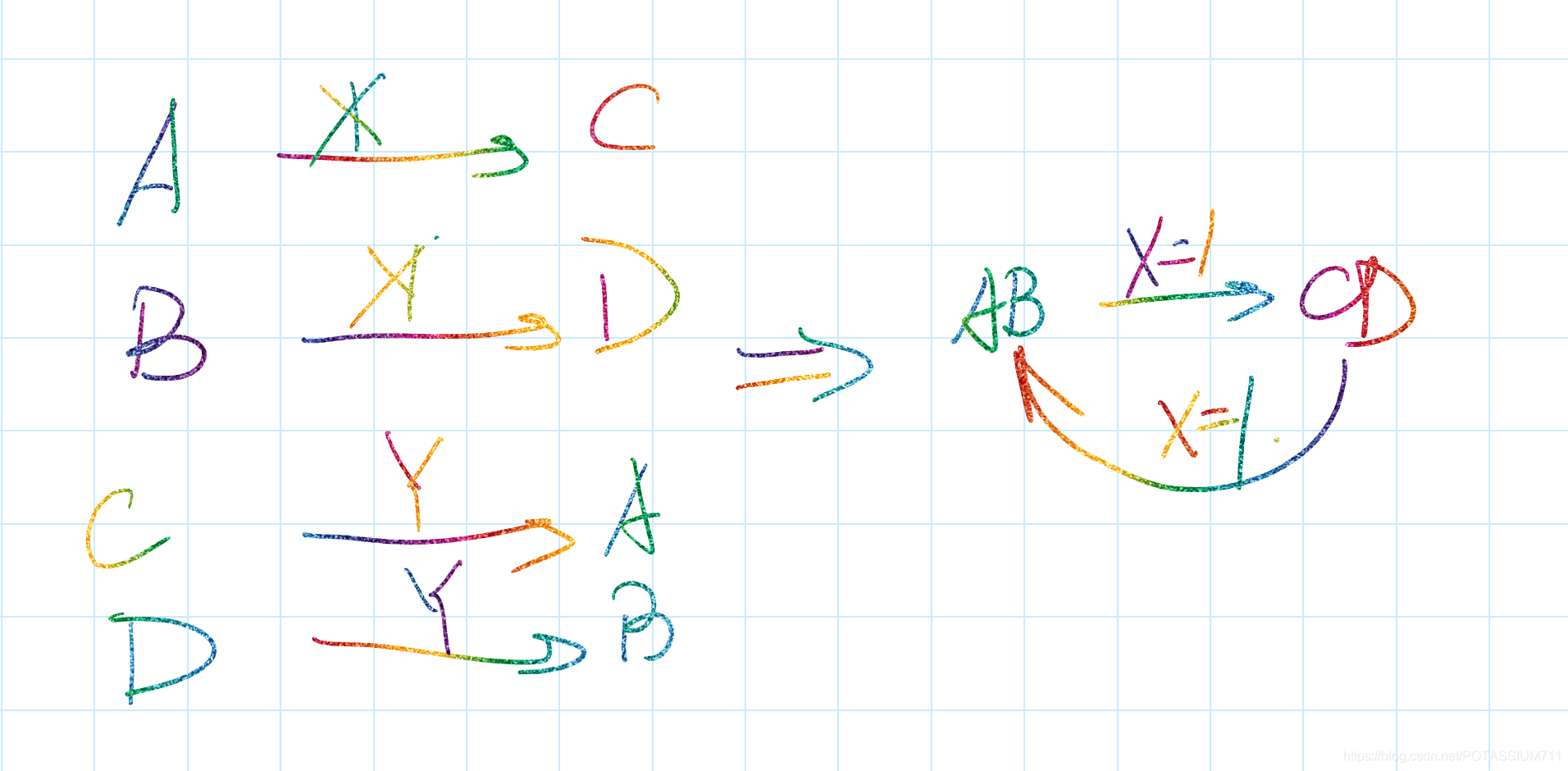 比如在这里,AB等价,CD等价.
比如在这里,AB等价,CD等价.
(Additional)(最大)等效类
等效类是指两两等效的状态的去重集合.例如
( S 1 , S 2 ) , ( S 2 , S 3 ) , ( S 1 , S 3 ) → { S 1 , S 2 , S 3 } (S_1,S_2),(S_2,S_3),(S_1,S_3)\rightarrow \{S_1,S_2,S_3\} (S1,S2),(S2,S3),(S1,S3)→{S1,S2,S3}
由于等效对有传递性,上述三个等效状态可认为S1等效于S3.
等效类是广义的概念,两个状态或多个状态均可以组成一个等效类,甚至一个状态也可以称为等效类。
最大等效类是指不被任何其它等效类包含的等效类。(强调独立性)
原始状态表的化简过程,就是寻找所有最大等效类的过 程,每个最大等效类中的状态合并为一个新的状态。
最后的状态都应该是最大等效类.
(Additional)隐含表,等效类的判定方式
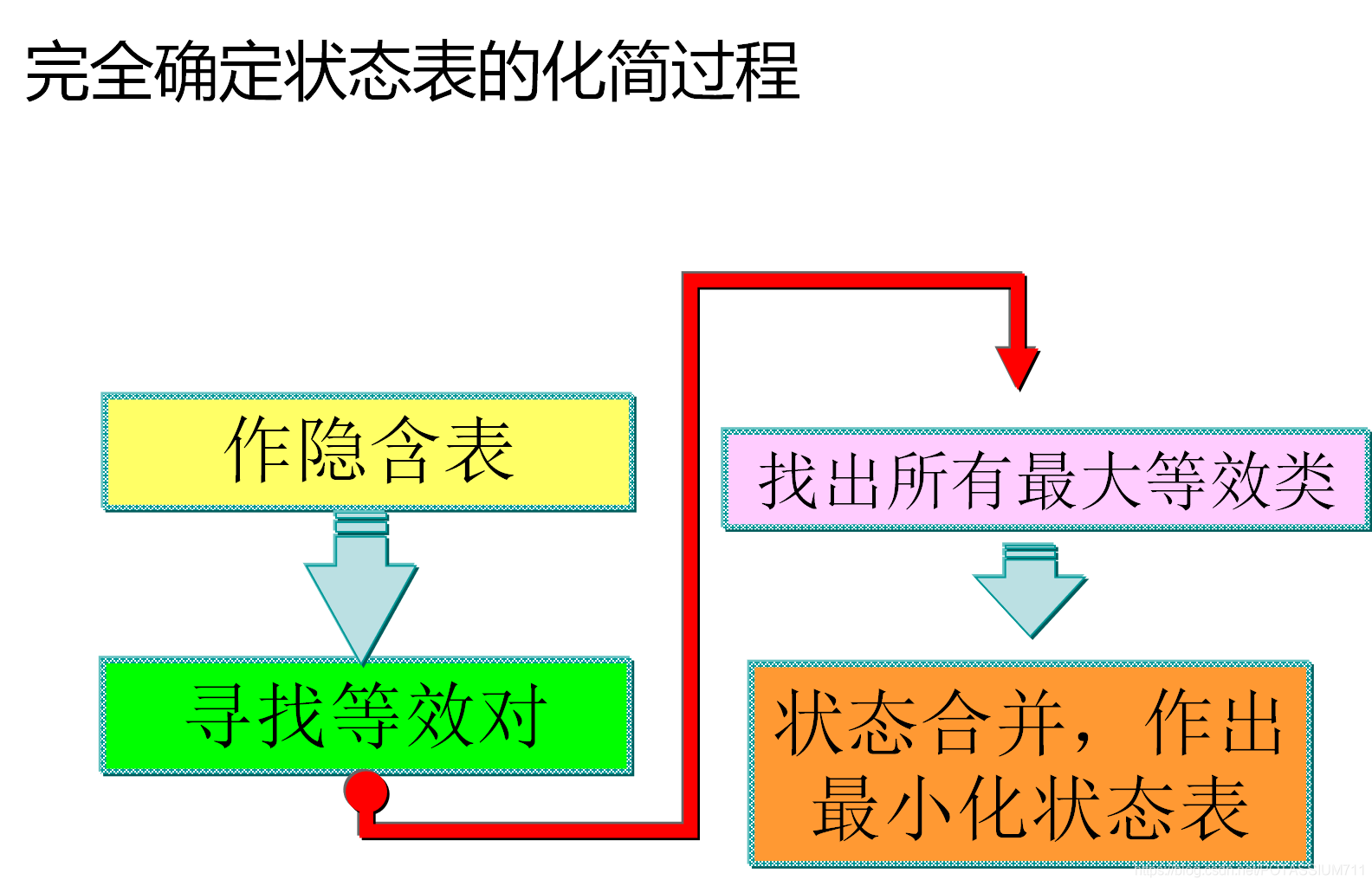 #### 隐含表
#### 隐含表
 #### 等效对的判定
#### 等效对的判定
按等效对判断规则,对原始状态表任意两个原态逐一检查和比较
将检查结果标注在隐含表中的相应方格内
等效:“√”; 不等效:“×” ;无法判断:填相关的状态对
关联比较确定所有状态是否等效.
检查每对时,可针对每一对画状态转移图.对于明显无关的可以略过.但要注意以下几种:
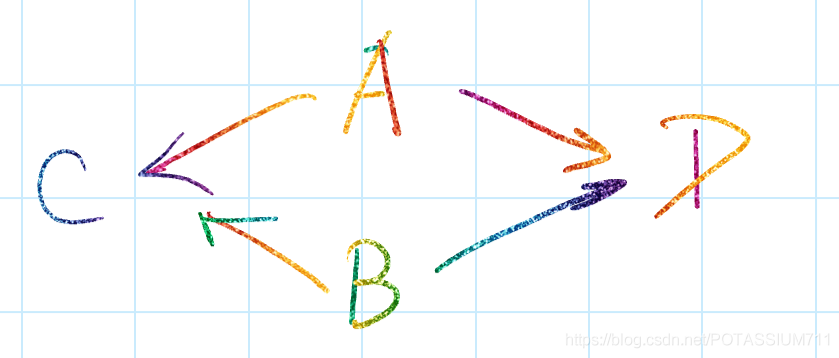
表格构型为:
| X | X ˉ \bar {X} Xˉ | |
|---|---|---|
| A | C/Y | D/Y |
| B | C/Y | D/Y |
这种构型在表上很明显,次态和输出都是一样的.
 这一种注意检查另外一组输入的输出和次态指向是不是一样的.如果是一样的就可以判定等效.否则留意分别指向的两个次态是否为等效.如果是,仍是等效对.
这一种注意检查另外一组输入的输出和次态指向是不是一样的.如果是一样的就可以判定等效.否则留意分别指向的两个次态是否为等效.如果是,仍是等效对.
表格构型为:
| X | X ˉ \bar {X} Xˉ | |
|---|---|---|
| A | B/Y | K/Y’ |
| B | A/Y | K/Y’ |

表格构型为:
| X | X ˉ \bar {X} Xˉ | |
|---|---|---|
| A | C/Y | / |
| B | D/Y | / |
| … | ||
| C | / | A/X |
| D | / | B/X |
注意:如果由于其他的原因,指向的两个不同状态之后被认为是等效,那么在其他的判定中仍认为这两个状态是一样的,这可能影响到等效对的判定.
状态分配
经过状态的合并之后得到了最少的状态数m,则可以得知需要用的触发器数n,n的值应该满足
2 n − 1 ≤ m ≤ 2 n 2^{n-1}\leq m \leq 2^{n} 2n−1≤m≤2n
状态的分配就是给化简后的各个状态分别分配一组代码。例如,化简后得到的状态有S0、S1、S2和S3,可知应该用2个触发器来实现,状态编码可以用二进制编码方式,令S0 = 00、S1 = 01、S2 = 10、S3 = 11,也可以用循环码来编码,令S0 = 00、S1 = 01、S2 = 11、S3= 10。
相邻分配法
- 次态相同,现态相邻。 相同输入条件下,次态相同的现态分配相邻二进制代码;
- 同一现态,次态相邻。 同一现态在相邻输入条件下的次态分配相邻二进制代码;
- 输出相同,现态相邻。 所有输入均具有相同输出的现态分配相邻二进制代码。
- 一般将初始状态分配“0”状态.
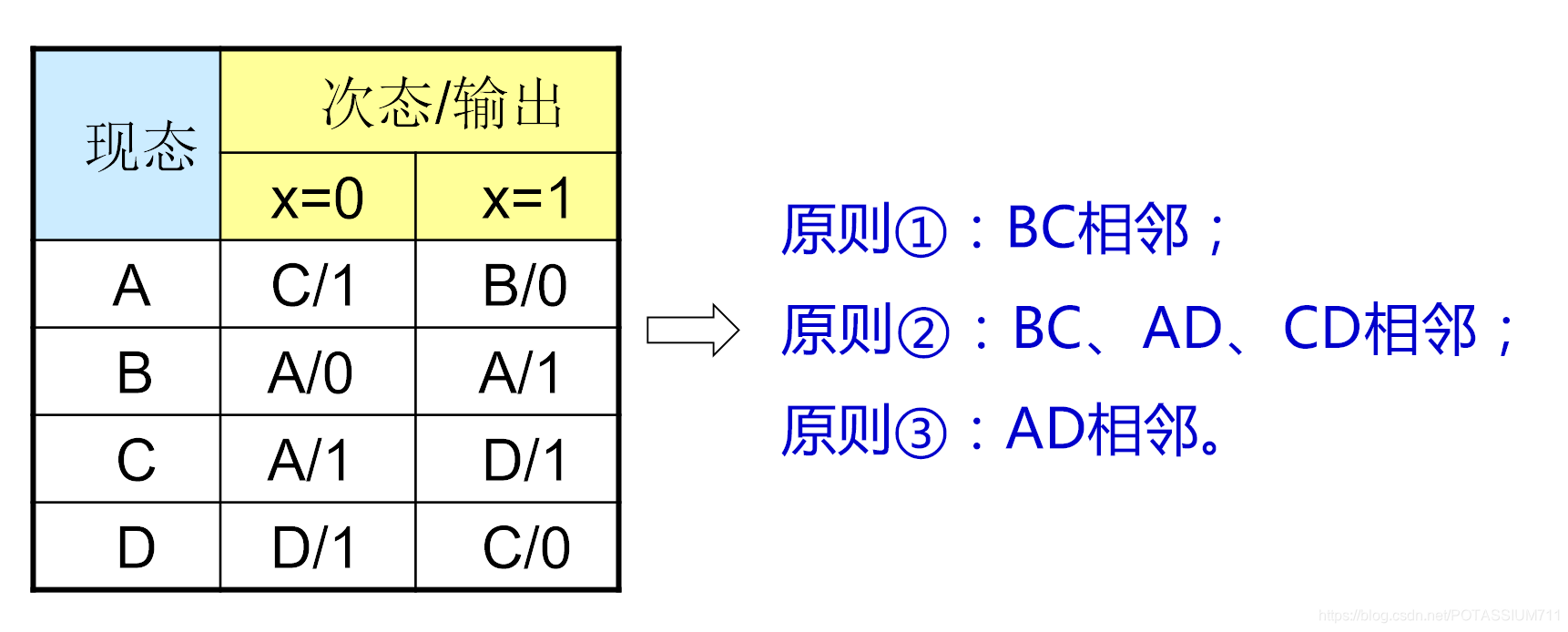
- 第一个基于同一输出的次态
- 第二个基于同一初态.
- 第三个基于相同的输入/输出对
卡诺图分配编码

- 确定初始状态A
- 在卡诺图上演绎上一步确定的相邻关系.
- 最后整理得到电路编辑用原始状态表.如下图:
求出状态方程和驱动方程及输出方程
根据二进制状态表和触发器激励表,求激励函数和输出函数的最简表达式.
一般分为两步:
- 列出激励函数和输出函数真值表;
- 用卡诺图化简后写出最简表达式。
- 详细方法参考上一篇.
自启动和挂起检查
-
电路万一偶然进入无效状态,如 果能在输入信号和时钟脉冲作用下自动进入有效状态,则称为 具有自恢复(自恢复)功能;否则,称为“挂起”。
-
电路万一处在无效状态,是 否会在输入信号和时钟脉冲作用下产生错误输出信号。
-
将偏离状态值代入状态转移方程中,检查这些偏离状态能否进入到正常得计数循环中去,如果能够进入,则说明所设计的电路可以自启动,否则不可以自启动,需要修改状态转移方程,电路也该作相应的修改。
-
检查无效状态的编码
-
讨论时只需检查卡诺图,便可知无效状态下的激励函数和输出函数取值,并推出相应次态和输出,进而作出 与设计方案对应的状态图或状态表,得出讨论结果。
也就是说,如果在状态流转图中无关状态编码不是"孤立的",就可以认为具有自启动(防挂起)功能.
Sample
例6.4.3 设计一个串行数据转换电路,已知串行数据输入端X所加的是两位8421BCD码,输出端为Y为两位串行循环码,用JK触发器实现此逻辑电路。
解:用组合逻辑电路的方法也可以实现代码转换,不过其实现的是并行码的转换,由于本题的输入和输出端只有一个,每输入一位数据都必须记忆,所以只能用时序逻辑电路的设计方法。
输入端X的两位串行8421BCD码数据分别为:00、01、10、11,输出端Y的两位串行循环码数据分别为:00、01、11、10,设计任务就是要将输入的8421BCD转换为循环码。即:
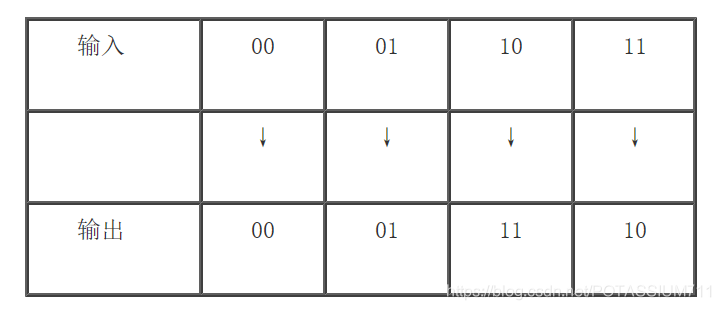
输入数据时,假设先输入高位数,然后输入低位数。设电路的初始状态为S0,输入数据X,加入时钟信号边沿,触发器状态发生翻转。第一次输入的数据(输入高位)只有两种可能性,分别时0和1,用状态S1和S2来分别记录这种新的状态,此时的输出Y分别为0和1。在第2次输入数据(输入低位)时分别又有两种可能,分别是0和1,对应得到的新的状态有4种,分别记作S3、S4、S5和S6,输出端Y的值分别为0、1、1和0,根据分析可以作出原始状态转换图为图6.4.15所示。
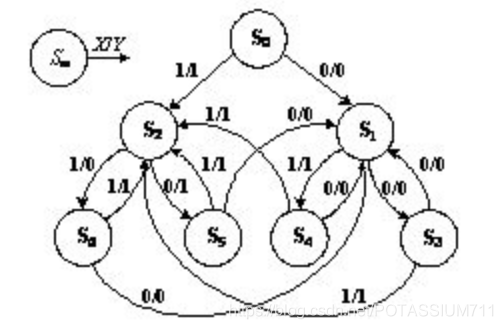
(第三排从右至左依次为3,4,5,6)
图6.4.15表示出了原始状态之间的转换关系。S1状态说明已经输入了一位高位数为0,输出则为0,S3状态说明输入数据的低位为0,输出则为0;处于S3状态时,如果再输入下一位数据为X= 0,则从S3状态转移到S1状态,说明输入数据的高位为0,输出为0,如果输入的数据为X= 1,则从S3状态转移到S2状态,说明输入数据的高位为1,输出为1。
当电路处于S1状态时,说明已经输入了一位高位数为0,输出为0,从状态S1转移到S4状态,说明又输入了一位低位数为1,输出则为1;处于S4状态时,如果再输入下一位数据为X= 0,则从S4状态转移到S1状态,说明输入数据的高位为0,输出为0,如果输入的数据为X= 1,则从S4状态转移到S2状态,说明输入数据的高位为1,输出为1。
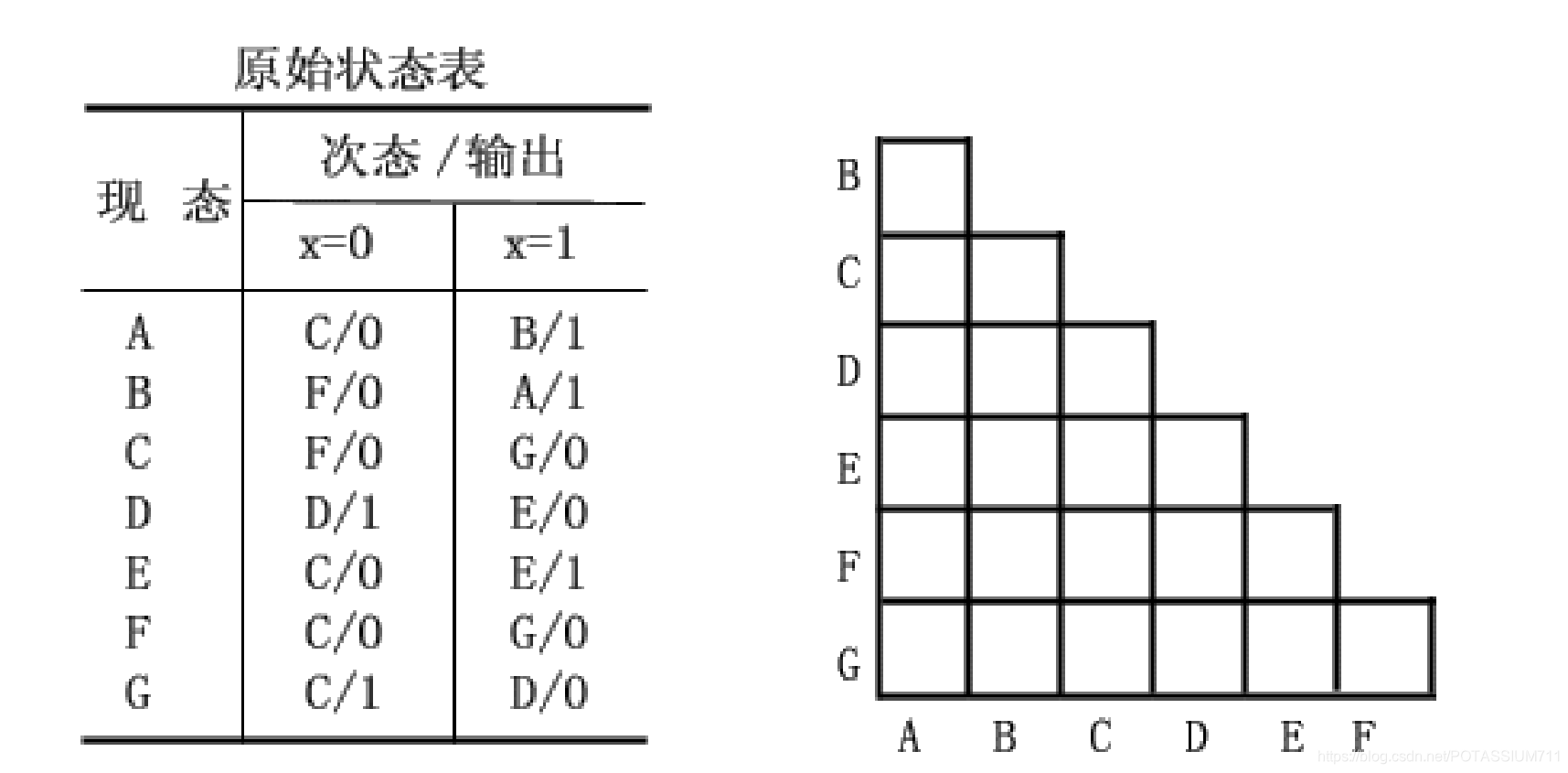
同样的可以得出状态S5和S6的转换关系。根据原始状态图可以画出原始状态转换表。如表6.4.1所示。
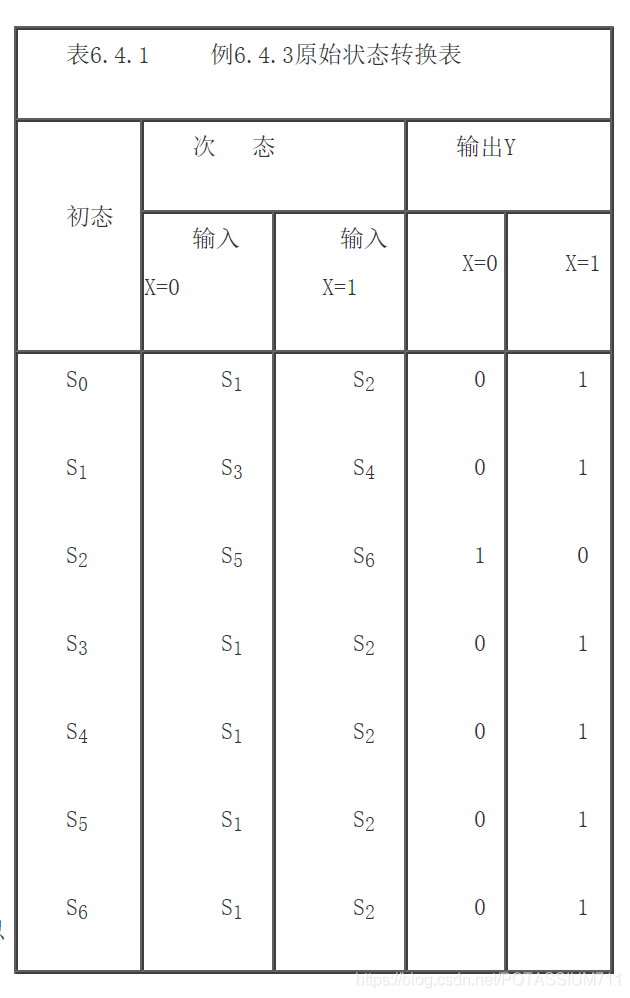
将原始状态图化简,合并等价的逻辑状态,寻找状态间的等价应该遵循时序电路设计方法中的第3点,为了可以方便地找出等价状态,可以采用隐含表的方法,
隐含表就是把原始状态表中的各个状态用图形的方法表示出来,便于查找等价状态的一种方法。隐含表为一个等边直角三角形网格,横向从左到依次右标记为第一个状态至倒数第二个状态,如图6.4.16(a)中的横向标记为S0、S1…S5,纵向从上到下依次标记为第二个状态至最后一个状态,如图6.4.16(a)中的纵向标记为S1、S2…S6。
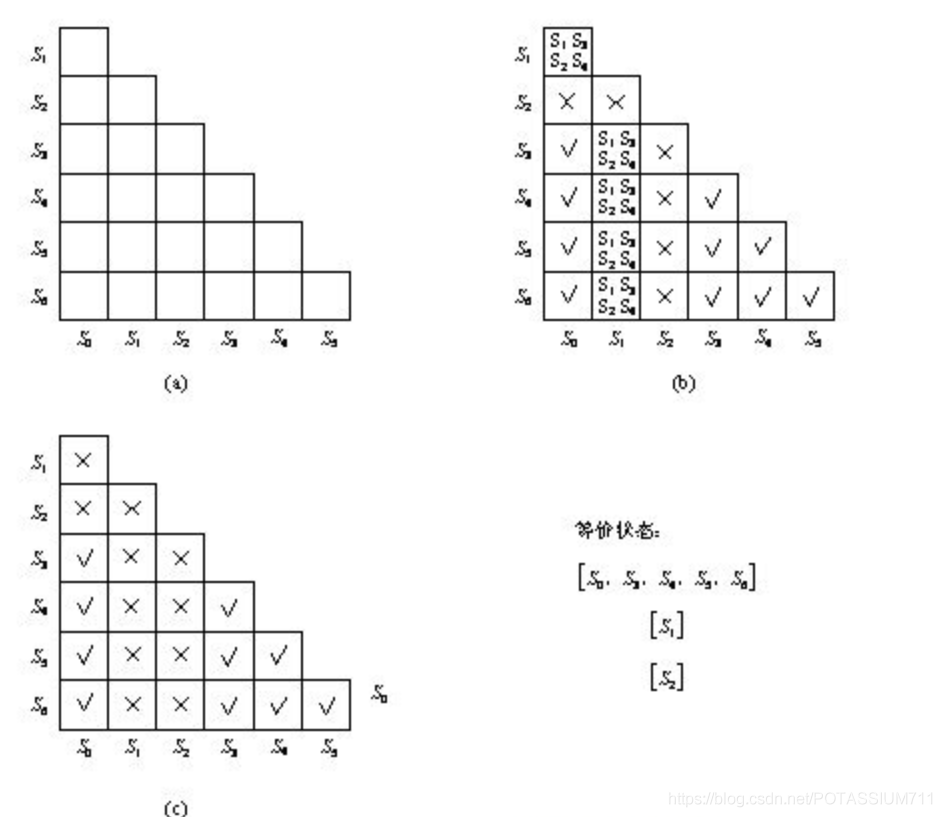
这样在可以在网格中记录原始状态中的两两对应关系,将它们间的等价关系填入网格中。如果两个状态满足等价关系,则在网格中记作“√”;如果两个状态间不满足等价关系,则在网格中记作“×”;如果两个状态是否等价取决于其他状态是否等价,则在网格中填入其他的状态。结合原始状态表,可以先将S0状态与其他6个状态进行比较,得到的等价关系记入图6.4.16(b)中,在图6.4.16(b)的S0对应的一列中,S0和S1的等价性取决于S1和S3、S2和S4是否等价,所以在其网格中填入的是状态S1.S3、S2.S4。依次将原始状态表中的状态进行比较,得到图6.4.16(b)的隐含表。
从图6.4.16(b)可以进一步判断等价状态,因为S2的输出结果与其他状态都不相同,所以状态S2与其他任一状态都不等价,比较其他的状态可以得到图6.4.16(c)
的全部状态等价关系。从化简的结果可以得到等价关系[S0 S3 S4 S5 S6]、[S1]、[S2]。
可见经过状态合并后的状态只有三个,可以用S0来代替状态S3、S4 、S5 、S6,化简后状态转换表,如表6.4.2所示。化简后的状态转换图如图6.4.17(a)所示。

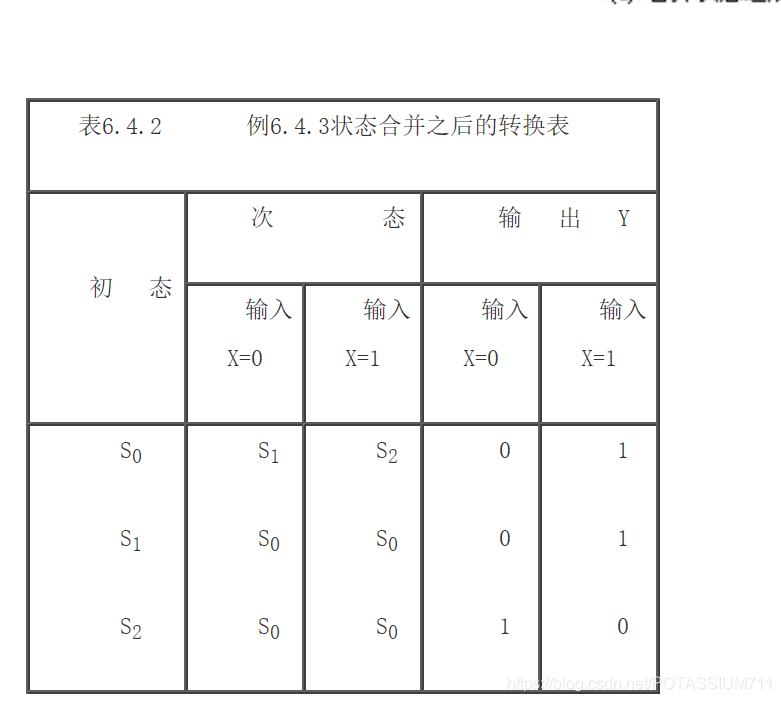
将状态S0、S1、S2进行编码,因为用到的只有3个状态,所以用两位二进制数表示即可。用00来表示状态S0,用01来表示状态S1,用11来表示状态S2。
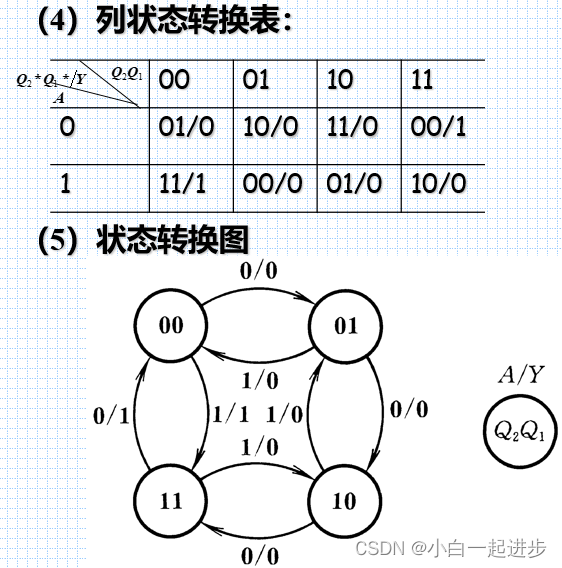
图6.4.17(b)为编码后的状态转换图。
根据编码后的状态转换图可以作出卡诺图如图6.4.18所示。
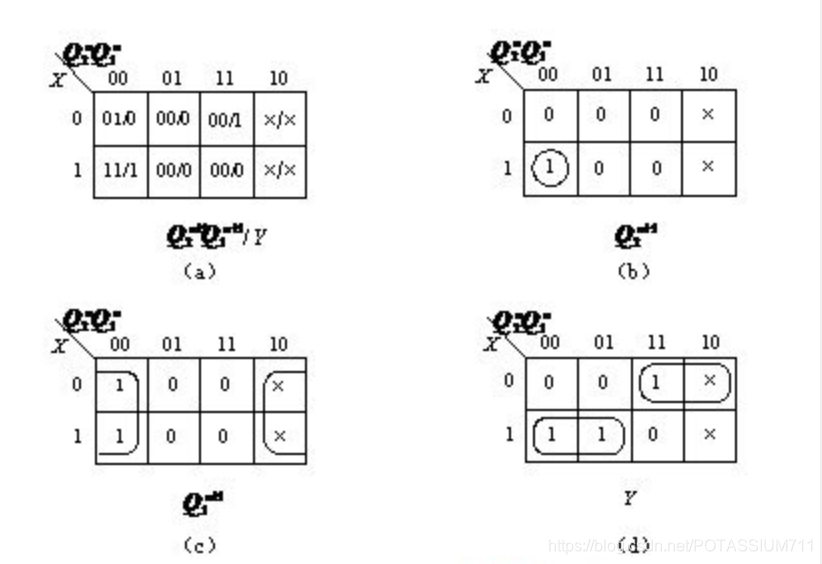
应用无关项化简卡诺图可得到触发器得状态转移方程
Q 1 n + 1 = Q ˉ 1 n Q 2 n + 1 = X ⋅ Q ˉ 1 n Q ˉ 2 n Q_1^{n+1}=\bar{Q}_1^n\\ Q_2^{n+1}=X\cdot \bar{Q}_1^n\bar{Q}_2^n Q1n+1=Qˉ1nQ2n+1=X⋅Qˉ1nQˉ2n
所以可以得到JK触发器得驱动方程为
J 1 = 1 , K 1 = 1 J 2 = X ⋅ Q ˉ 1 n , K 2 = 1 J_1=1,K_1=1\\ J_2=X\cdot \bar{Q}_1^n,K_2=1 J1=1,K1=1J2=X⋅Qˉ1n,K2=1
根据(6.4.9)式的输出方程和(6.4.11)式的驱动方程,可以画出逻辑电路图6.4.20所示。
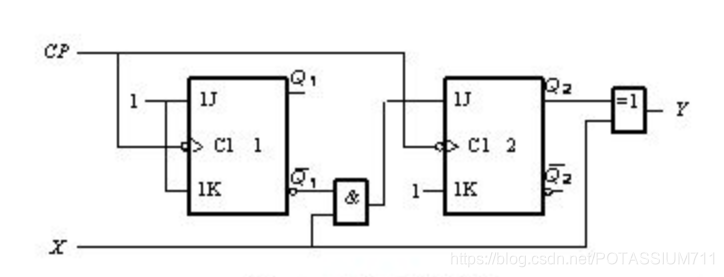
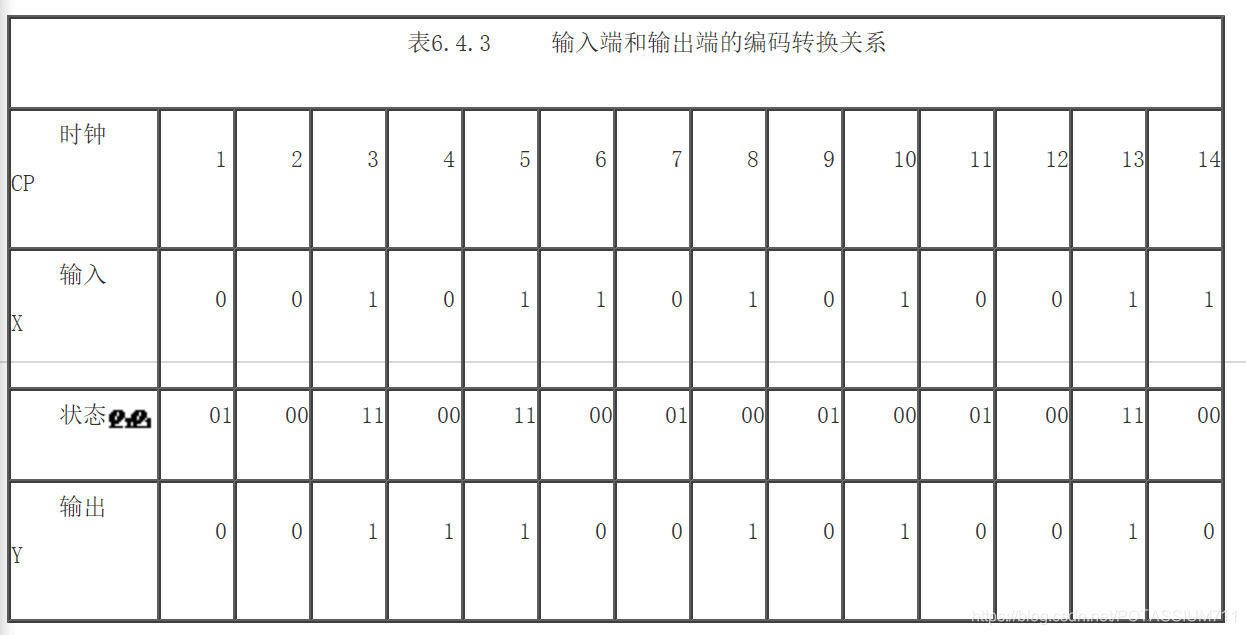
根据设计的逻辑电路,设电路的处于初始状态时,触发器输出都为0,现将输入端连续输入数据00 10 11 01 01 00 11(先输入高位),可以用表6.4.3来表示输出端对应得到的变换代码。