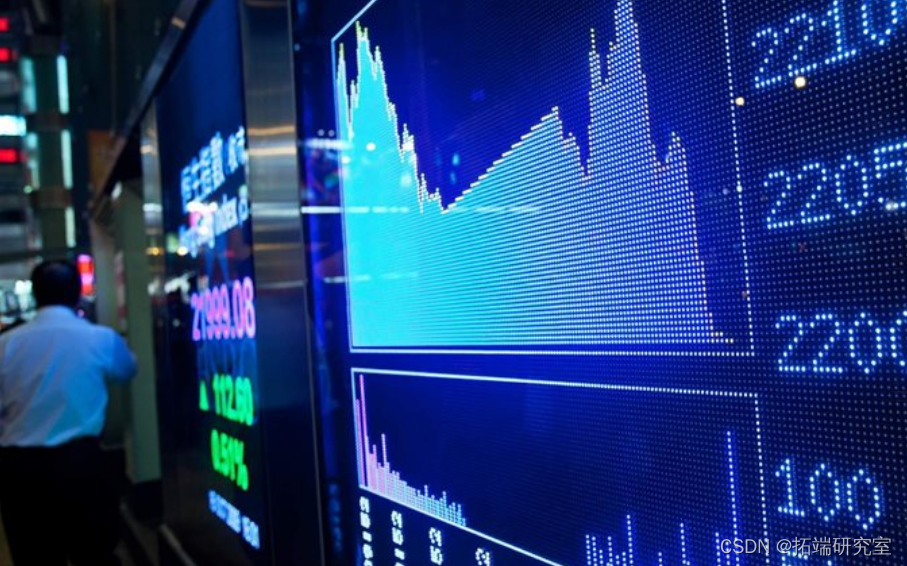
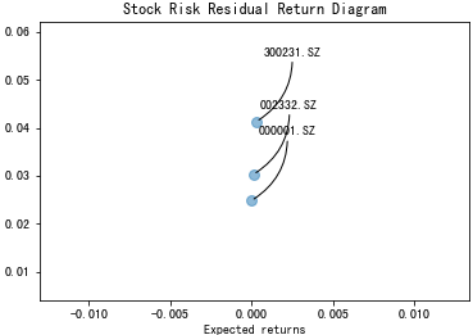
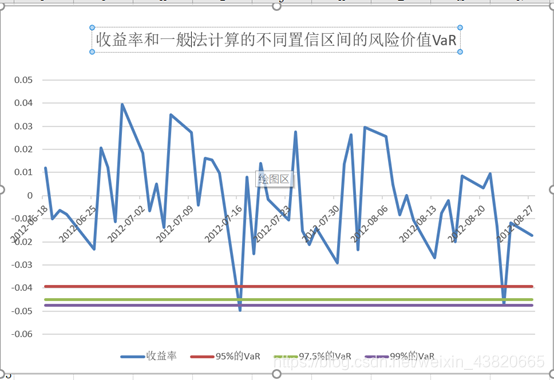
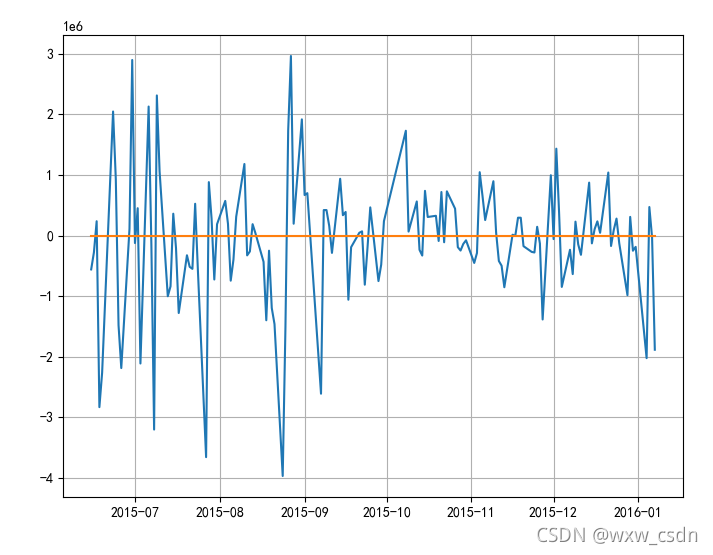
风险价值（VaR）：即在市场正常波动的条件下，在一定概率水平P%下，某一金融资产或金融资产组合的VaR是在未来特定一段时间Δt内最大可能损失。 现在我们使用蒙特卡罗模拟法进行风险价值的估算。简单来说，蒙特卡罗模拟法即运用历史数据对未来进行多次模拟，以求得未来股价结果的概率分布。蒙特卡罗模拟法的公式如下, 其中S为股票的价格，为股价变动大小(有正负)，μ为期望收益率(平均)，Δt为时间间隔，σ为股票风险，ε为随机变量。将S移项可得：

          

将S移项可得： 

表示股价的波动大小是由前一天的波动期望和一个服从正态分布的随机波动影响

所以下一个的股价可以表示为

 

以美的股价为例，先贴上程序代码如下，回头有空再详细解析：

#环境&数据准备
import sys as sy
import numpy as np
import pandas as pd
import tushare as ts
import pyecharts as pye
from sklearn import datasets as ds
import matplotlib as mpl
from matplotlib import pyplot as plt
import seaborn as sns
import pyecharts as pyedef stock_monte_carlo(start_price,days,mu,sigma):''' This function takes in starting stock price, days of simulation,mu,sigma, and returns simulated price array'''# Define a price arrayprice = np.zeros(days)price[0] = start_price# Schok and Driftshock = np.zeros(days)drift = np.zeros(days)# Run price array for number of daysfor x in range(1,days):# 假设股票的价格波动可以分为两部分，第一部分为drift，即股票会根据收益率波动，第二部分为shock，即随机波动shock[x] = np.random.normal(loc=mu * dt, scale=sigma * np.sqrt(dt))# Calculate Driftdrift[x] = mu * dt# 当天价格 = 前一天价格 + 价格波动#其中价格波动 = 前一天价格×（drift + shock）price[x] = price[x-1] + (price[x-1] * (drift[x] + shock[x]))return price#读入美的“000333”2017-01-01 到 2018-11-08复权后数据
df = ts.get_h_data('000333', start='2017-01-01', end='2018-11-8') 
#计算日均收益率
df1 = df['close'].sort_index(ascending=True)
df1 = pd.DataFrame(df1)
df1['date'] = df1.index
df1['date'] = df1[['date']].astype(str)
df1["rev"]= df1.close.diff(1)
df1["last_close"]= df1.close.shift(1)
df1["rev_rate"]= df1["rev"]/df1["last_close"]
df1 = df1.dropna()
print(df1.head(10))# 设定365天
days = 365
# Now our delta
dt = 1/days
# Now let's grab our mu (drift) from the expected return data we got for AAPL
mu = df1["rev_rate"].mean()
# Now let's grab the volatility of the stock from the std() of the average return
sigma = df1["rev_rate"].std()# Get start price 
start_price = 40.63
runs = 1000
simulations = np.zeros(runs)
np.set_printoptions(threshold=5)for run in range(runs):tmpAr = stock_monte_carlo(start_price,days,mu,sigma)simulations[run] = tmpAr[days-1];plt.plot(tmpAr)del tmpArplt.xlabel("Days")
plt.ylabel("Price")  
plt.title('Monte Carlo Analysis for Tesla')
plt.show()