最近我们被客户要求撰写关于风险价值VaR的研究报告，包括一些图形和统计输出。 

什么是风险价值（VaR）？

风险价值 (VaR) 是一种统计数据，用于量化公司、投资组合在特定时间范围内可能发生的财务损失程度。该指标最常被投资银行和商业银行用来确定其机构投资组合中潜在损失的程度和概率。

视频：风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例

，时长10:03

相关视频：马尔可夫链蒙特卡罗方法MCMC原理与R语言实现

，时长08:47

风险管理人员使用 VaR 来衡量和控制风险暴露水平。人们可以将 VaR 计算应用于特定或整个投资组合，或使用它们来衡量公司范围内的风险敞口。

关键要点

• 风险价值 (VaR) 是一种量化公司或投资潜在损失风险的方法。

• 该度量可以通过多种方式计算，包括历史、方差-协方差和蒙特卡洛方法。

• 尽管 VaR 作为一种风险度量在行业中很受欢迎，但它也存在不足之处。

了解风险价值 (VaR)

VaR 模型确定了被评估实体的潜在损失以及发生定义损失的概率。一种方法是通过评估潜在损失的数量、损失数量的发生概率和时间范围来衡量 VaR。

例如，一家金融公司可能会确定一项资产的 3% 的 1 个月 VaR 为 2%，这表示资产在 1 个月的时间范围内价值下降 2% 的可能性为 3%。将 3% 的发生几率转换为每日比率后，每月 1 天发生 2% 的损失几率。

风险价值方法论

计算 VaR 的方法主要有 3 种。

第一种是历史方法，它着眼于一个人之前的收益历史。

第二种是方差-协方差法。这种方法假设收益和损失是正态分布的。

最后一种方法是进行蒙特卡罗模拟。该技术使用计算模型来模拟数百或数千次可能迭代的期望收益。

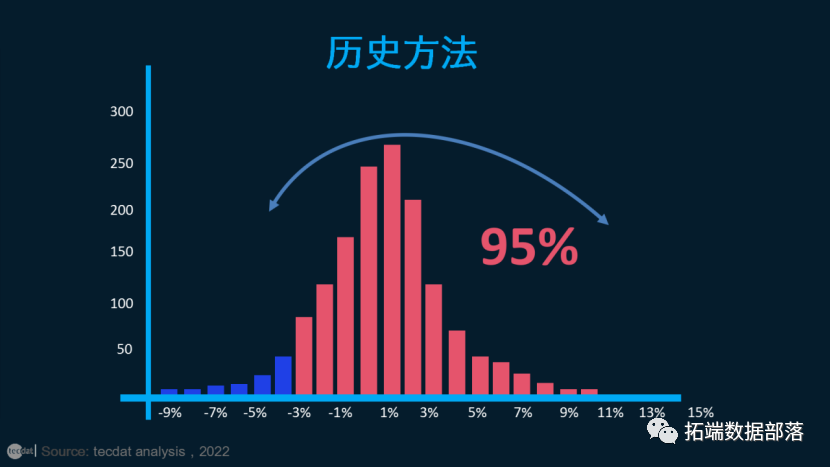
历史方法

历史方法只是重新组织实际的历史收益，将它们从最差到最好的顺序排列。然后从风险的角度假设历史会重演。

作为一个历史例子，让我们看一下纳斯达克 100 ETF。如果我们计算每天的收益，我们会产生丰富的数据设置超过 1,400 点。让我们将它们放在一个直方图中。例如，在直方图的最高点（最高柱），有超过 250 天的日收益率在 0% 到 1% 之间。在最右边，你几乎看不到一个 10% 的小条；它代表了 5 年多内的一天（2000 年 1 月），每日收益率达到了惊人的 9.4%。4

请注意构成直方图“左尾”的红色条。这些是每日收益率最低的 5%（因为收益率是从左到右排序的，所以最差的总是“左尾”）。红条从每日损失 4% 到 8% 不等。因为这些是所有每日收益中最差的 5%，我们可以有 95% 的信心说，最差的每日损失不会超过 4%。换句话说，我们有 95% 的信心预计我们的收益将超过 -4%。简而言之，这就是 VaR。

方差-协方差法，也称为参数法

该方法假设股票收益是正态分布的。换句话说，它只要求我们估计两个因素——期望（或平均）收益和标准差——这使我们能够绘制正态分布曲线。在这里，我们根据相同的实际收益数据 绘制正态曲线：

方差-协方差背后的思想类似于历史方法背后的思想——除了我们使用熟悉的曲线而不是实际数据。正态曲线的优点是我们可以自动知道最差的 5% 和 1% 在曲线上的位置。它们是我们期望的置信度和标准偏差的函数。

信心	# 标准偏差 (σ)
95%（高）	- 1.65 x σ
99%（非常高）	- 2.33 x σ

上面的蓝色曲线是实际每日标准差，即2.64%。平均每日收益恰好接近于零，因此为了说明目的，我们将假设平均收益为零。以下是将实际标准差代入上述公式的结果：

信心	σ	计算	等于
95%（高）	- 1.65 x σ	- 1.65 x (2.64%) =	-4.36%
99%（非常高）	- 2.33 x σ	- 2.33 x (2.64%) =	-6.15%

我们有95%的信心说，最差的每日损失不会超过-4.36%

蒙特卡洛模拟

第三种方法涉及为未来股票价格收益开发一个模型，并通过该模型运行多个假设试验。蒙特卡洛模拟是指任何随机生成试验的方法，但它本身并没有告诉我们任何有关基础方法的信息 。

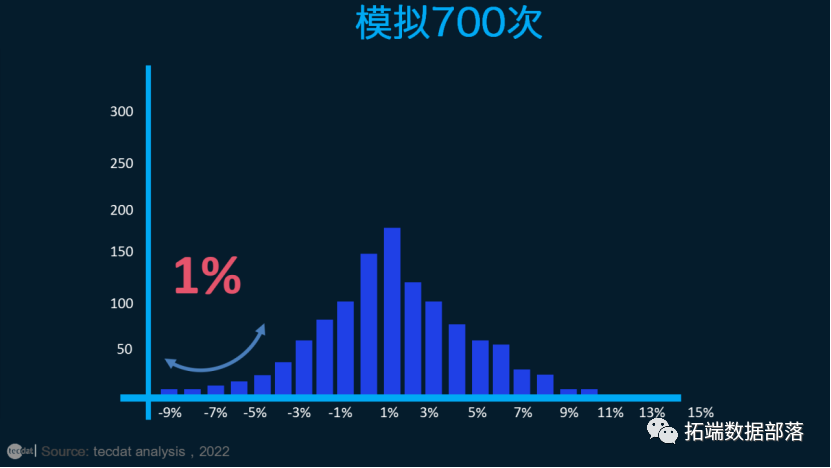
对于大多数用户来说，蒙特卡洛模拟相当于一个随机、概率结果的“黑匣子”生成器。在不深入细节的情况下，我们根据其历史交易模式进行了蒙特卡罗模拟。在我们的模拟中，进行了 700 次试验。如果我们再次运行它，我们会得到不同的结果——尽管差异很可能会缩小。

总而言之，我们对月收益进行了 700 次假设试验。其中，5个结果在-5%和-7%之间；2个在 -7% 和 -9% 之间。这意味着最差的7个结果（即最差的 1%）低于 -5%。因此，蒙特卡罗模拟得出以下 VaR 类型的结论：在 99% 的置信度下，我们预计在任何给定月份的损失不会超过 5%。

风险价值 (VaR) 的优势

1. 易于理解

风险价值是一个数字，表示给定投资组合的风险程度。风险价值以价格单位或百分比来衡量。这使得 VaR 的解释和理解相对简单。

2. 适用性

风险价值适用于所有类型的资产——债券、股票、衍生品、货币等。因此，不同的银行和金融机构可以很容易地使用 VaR 来评估不同投资的盈利能力和风险，并根据 VaR 分配风险.

3.通用

风险价值数字被广泛使用，因此它是购买、出售或推荐资产的公认标准。

风险价值的限制

1. 大型投资组合

计算投资组合的风险价值不仅需要计算每种资产的风险和收益，还需要计算它们之间的相关性。因此，投资组合中资产的数量或多样性越大，计算 VaR 的难度就越大。

2.方法不同

计算 VaR 的不同方法可能导致相同投资组合的不同结果。

3. 假设

VaR 的计算需要做出一些假设并将其用作输入。如果假设无效，那么 VaR 数字也无效。

如何使用Python通过蒙特卡洛模拟自动计算风险值（VaR）来管理投资组合或股票的金融风险？

我们将首先通过导入所需的库和函数

#导入所有需要的库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

为了我们项目的目的，我考虑了过去两年的 股票。

 for i in range(len):  web.get_data(tickers\[i\] 
stocks.tail()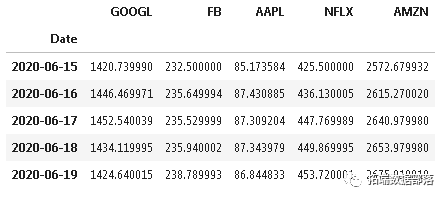

下一步，我们将计算每个资产的组合权重。可以通过实现最大夏普比率来计算资产权重。

#年化收益率
historical_return(stocks)
#投资组合的样本方差
sample_cov#夏普比率
EffFro(mu, Sigma, weight_bounds=(0,1)) #负数的权重界限允许做空股票
max_sharpe() #可以使用增加目标来确保单个股票的最小零权重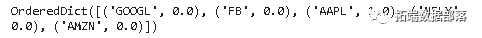

最大夏普比率的资产权重

资产权重将被用于计算投资组合的期望收益。

#VaR计算
rx2 = \[\]#换为最大夏普比率的资产权重
list(sharpe.values())

现在，我们将把投资组合的股票价格转换为累计收益，这也可以被视为本项目的持有期收益（HPR）。

   tick  = (tick  +1).cumprod()

#画出所有股票的累积/HPR的图形
tick\[col\].plot()plt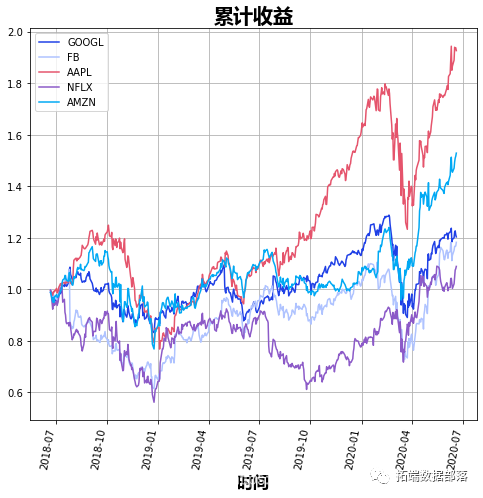

现在，我们将挑选出每个资产的最新HPR，并使用.dot()函数将收益率与计算出的资产权重相乘。

sigma = pre.std()
price=price.dot(sh_wt) #计算加权值

在计算了投资组合的期望收益和波动率（期望收益的标准差）后，我们将设置并运行蒙特卡洛模拟。我使用的时间是1440（一天中的分钟数），模拟运行20,000次。时间步长可以根据要求改变。我使用了一个95%的置信区间。

for j in range(20000): #20000次模拟运行(rtn/Time,sigma/ sqrt(Time),Time)
plt(np.percentile(daily_returns,5)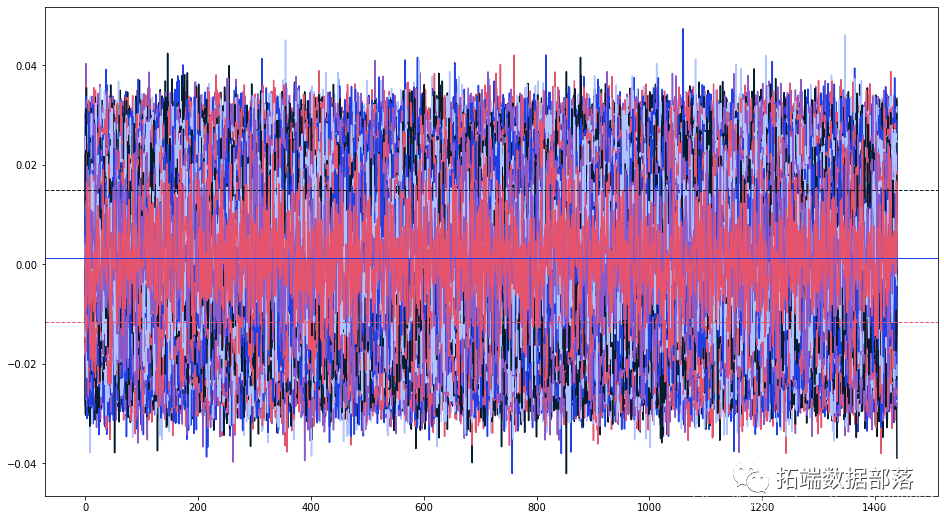

1440分钟内一天的收益范围 | 红色 - 最小损失 | 黑色 - 最小收益

将收益率的分布图可视化，我们可以看到以下图表

plt.hist(returns)
plt.show()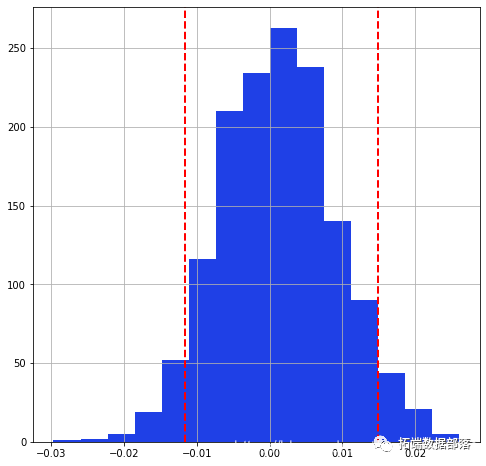

输出上限和下限的准确值，并假设我们的投资组合价值为1000元，我们将计算出应该保留的资金数额弥补我们的最低损失。

print(percentile( returns,5),percentile( returns,95)) VaR - 在5%的概率下，最小损失为5.7%，同样，在5%的概率下，收益可以高于15%

每天的最低损失是1.29%，概率为5%。

所得金额将标志着每天弥补你的损失所需的金额。这个结果也可以解释为你的投资组合在5%的概率下将面临的最低损失。

总结

上面的方法显示了我们如何计算投资组合的风险价值（VaR）。对于使用现代投资组合理论（MPT）计算一定数量的投资组合，有助于巩固你对投资组合分析和优化的理解。最后，VaR与蒙特卡洛模拟模型配合使用，也可用于通过股价预测损失和收益。这可以通过将产生的每日收益值与各自股票的最终价格相乘来实现。