最近我们被客户要求撰写关于风险价值（VaR）的研究报告，包括一些图形和统计输出。

如何使用Python通过蒙特卡洛模拟自动计算风险值（VaR）来管理投资组合或股票的金融风险。

金融和投资组合风险管理中的VaR？

VaR是 "风险价值 "的缩写，是许多公司和银行用来确定其公司内部金融风险水平的工具。风险值是为公司的投资而计算的，也可能是为检查银行或公司所管理的投资组合的风险水平。

 视频：风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例

，时长10:03

相关视频：马尔可夫链蒙特卡罗方法MCMC原理与R语言实现

，时长08:47

该计算可以被认为是一种统计方法。它也可以简化为以下语句  

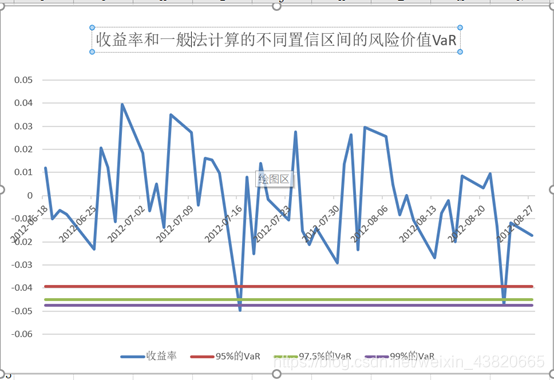
风险值是在一定的概率水平（置信区间）下将产生的最小损失或在一定的概率水平下将实现的最大损失。

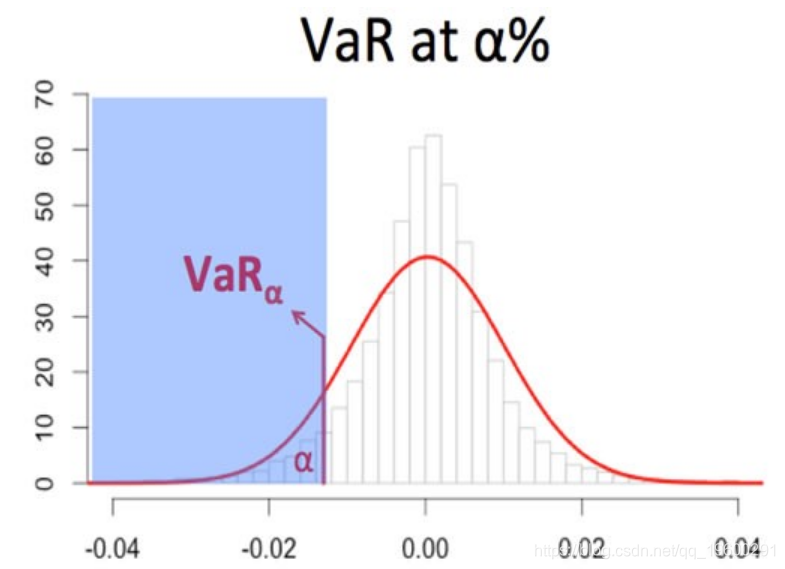
上图显示了一个公司在α%的置信水平下可能面临的最大损失。在个人层面上，VaR可以帮助你预测或分析你的投资组合可能面临的最大损失。

蒙特卡洛模拟

蒙特卡洛模型是Stanislaw Ulam和John Neumann的心血结晶，他们在第二次世界大战后开发了这个模型。该模型是以摩纳哥的一个赌博城市命名的，这是因为赌博中存在机会和随机性。

蒙特卡洛模拟是一个概率模型，它使用产生的随机变量与经济因素（期望收益率、波动率），来预测结果。该模型经常被用来计算风险和不确定性。

我们现在将使用蒙特卡洛模拟为我们的资产组合生成一组预测收益，这将有助于我们找出我们投资的风险值。

---

在Python中计算VaR

我们将首先通过导入所需的库和函数

#导入所有需要的库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

为了我们项目的目的，我考虑了过去两年的 股票。

 
for i in range(len):  web.get_data(tickers[i] 
stocks.tail()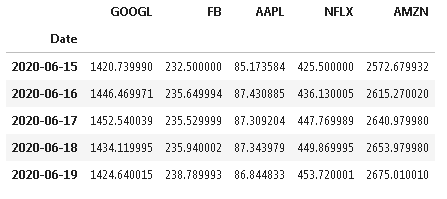

 

下一步，我们将计算每个资产的组合权重。可以通过实现最大夏普比率来计算资产权重。

#年化收益率
historical_return(stocks)
#投资组合的样本方差
sample_cov#夏普比率
EffFro(mu, Sigma, weight_bounds=(0,1)) #负数的权重界限允许做空股票
max_sharpe() #可以使用增加目标来确保单个股票的最小零权重

最大夏普比率的资产权重

资产权重将被用于计算投资组合的期望收益。

#VaR计算
rx2 = []#换为最大夏普比率的资产权重
list(sharpe.values())

现在，我们将把投资组合的股票价格转换为累计收益，这也可以被视为本项目的持有期收益（HPR）。

   tick  = (tick  +1).cumprod()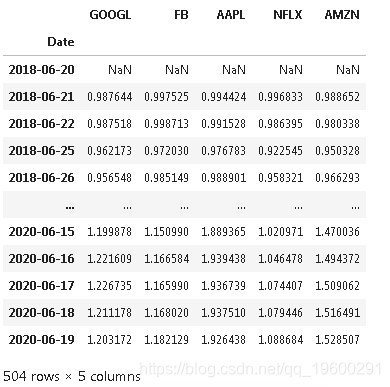

#画出所有股票的累积/HPR的图形
tick[col].plot()plt

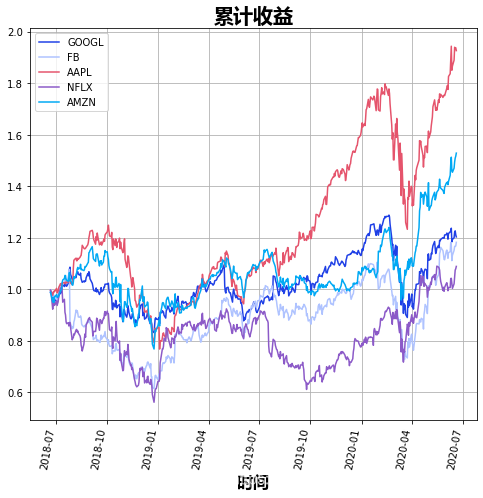
现在，我们将挑选出每个资产的最新HPR，并使用.dot()函数将收益率与计算出的资产权重相乘。

sigma = pre.std()
price=price.dot(sh_wt) #计算加权值

在计算了投资组合的期望收益和波动率（期望收益的标准差）后，我们将设置并运行蒙特卡洛模拟。我使用的时间是1440（一天中的分钟数），模拟运行20,000次。时间步长可以根据要求改变。我使用了一个95%的置信区间。

for j in range(20000): #20000次模拟运行(rtn/Time,sigma/ sqrt(Time),Time)
plt(np.percentile(daily_returns,5)

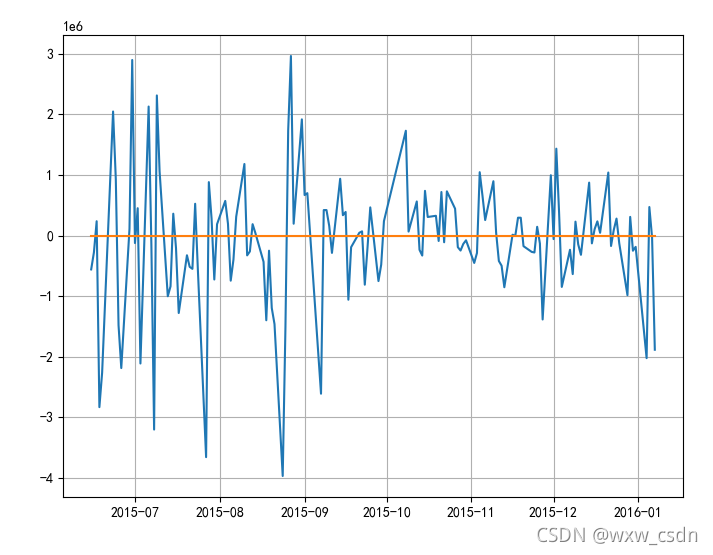
1440分钟内一天的收益范围 | 红色 - 最小损失 | 绿色 - 最小收益

将收益率的分布图可视化，我们可以看到以下图表

plt.hist(returns)
plt.show()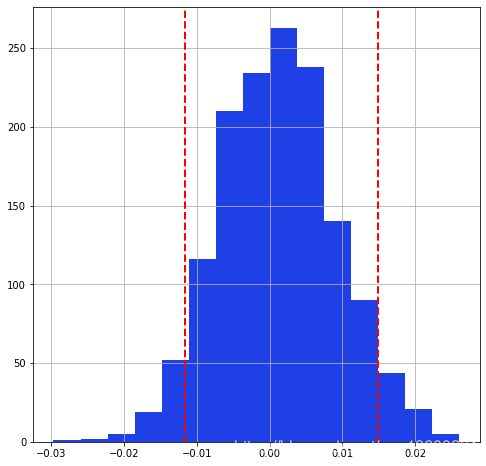

输出上限和下限的准确值，并假设我们的投资组合价值为1000元，我们将计算出应该保留的资金数额弥补我们的最低损失。

print(percentile( returns,5),percentile( returns,95)) VaR - 在5%的概率下，最小损失为5.7%，同样，在5%的概率下，收益可以高于15% 

每天的最低损失是1.29%，概率为5%。

所得金额将标志着每天弥补你的损失所需的金额。这个结果也可以解释为你的投资组合在5%的概率下将面临的最低损失。

总结

上面的方法显示了我们如何计算投资组合的风险价值（VaR）。对于使用现代投资组合理论（MPT）计算一定数量的投资组合，有助于巩固你对投资组合分析和优化的理解。最后，VaR与蒙特卡洛模拟模型配合使用，也可用于通过股价预测损失和收益。这可以通过将产生的每日收益值与各自股票的最终价格相乘来实现。

---