前言

第六章堆排序使用了普通的二叉堆性质。其基本操作性能相当好，但union性能相当差。

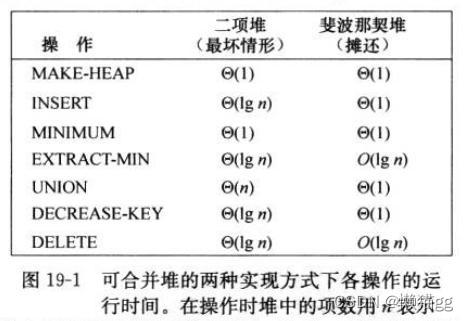
对于一些图算法问题，EXTRACT-MIN 和DELETE操作次数远远小于DECREASE-KEY。因此有了斐波那契堆。

斐波那契堆结构

斐波那契堆是一系列具有最小堆序的有根树的集合。也就是说，每棵树均遵循最小堆性质：每个结点的关键字大于或等于它的父结点的关键字。

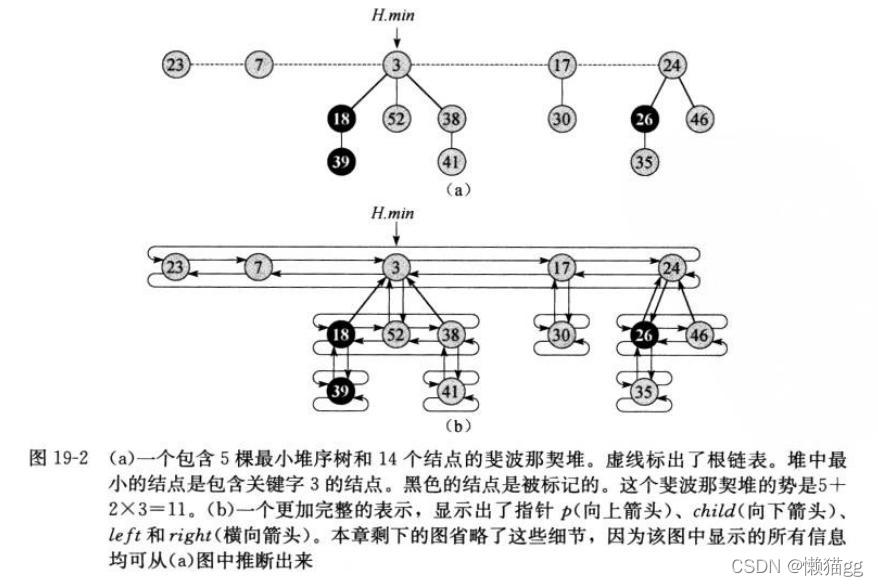
• 每个结点x包含一个指向它父结点的指针x.p和一个指向它的某一个孩子的指针x.child。x的所有孩子被链接成一个环形的双向链表，称为x的孩子链表。
• 孩子链表中的每个孩子y均有指针y.left和y.right，分别指向y的左兄弟和右兄弟。如果y是仅有的一个孩子，则y.left ＝ y.right ＝y。
• 结点x的孩子链表中的孩子数目储存在x.degree。
• 布尔值属性x.mark指示结点x自从上一次成为另一个结点的孩子后，是否失去过孩子。
• 通过指针H.min来访问一个给定的斐波那契堆H，该指针指向具有最小关键字的树的根结点，我们把这个结点称为斐波那契堆的最小结点。
• 如果一个斐波那契堆H是空的，那个H.min为NIL。
• H.n表示H中当前的结点数目。

可合并堆操作

创建一个新的斐波那契堆

创建一个空的H，Make-Fib-Heap分配并返回一个Fib对象H，其中H.n = 0和H.min = NIL，H中不存在树。

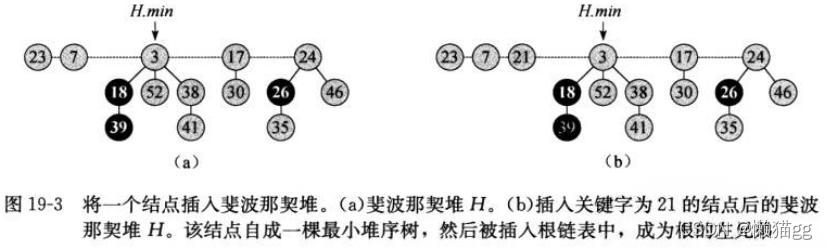
插入一个结点

直接将结点插入根连表中，如果是最小点则将H.min指向它

Fib-Heap-Insert(H, x)x.degree = 0x.p = NILx.child = NILx.mark = FALSEif H.min == NILcreate a root list for H containing just xH.min = xelseinsert x into H's root listif x.key < H.min.keyH.min = xH.n = H.n + 1

寻找最小结点

最小结点可通过H.min得到。

两个斐波那契堆的合并

将H1和H2的根链表链接，然后确定新的最小结点。之后，销毁H1和H2,表示H1和H2的对象将不再使用。

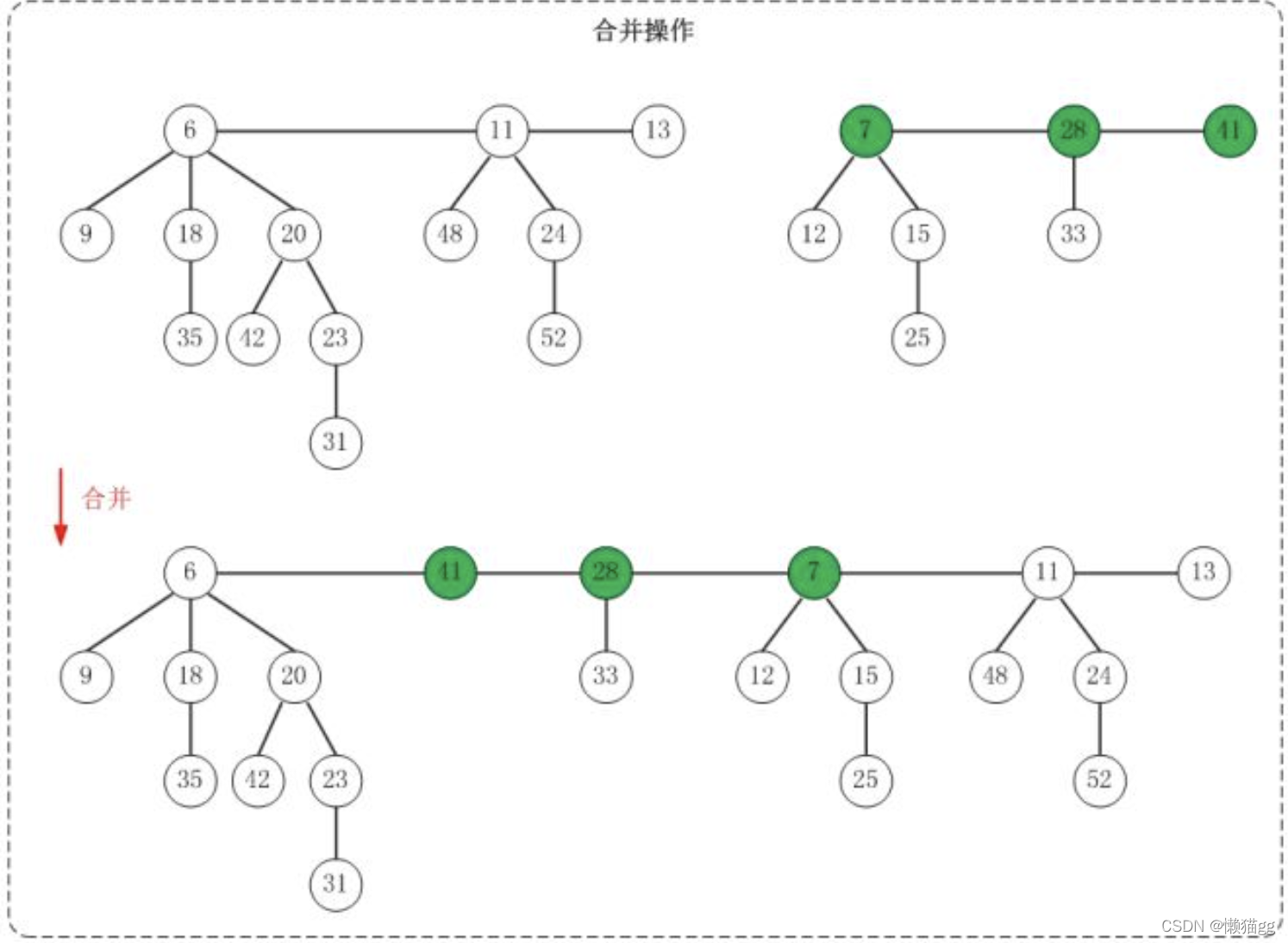
Fib-Heap-Union(H1, H2)H = Make-Fib-Heap()H.min = H1.minconcatenate the root list of H2 with the root list of Hif (H1.min == NIL) or (H2.min != NIL and H2.min.key < H1.min.key)H.min = H2.minH.n = H1.n + H2.nreturn H

抽取最小结点

1. 将要抽取的最小结点子树都直串在根表中
2. 合并所有degree相同的树，直到没有

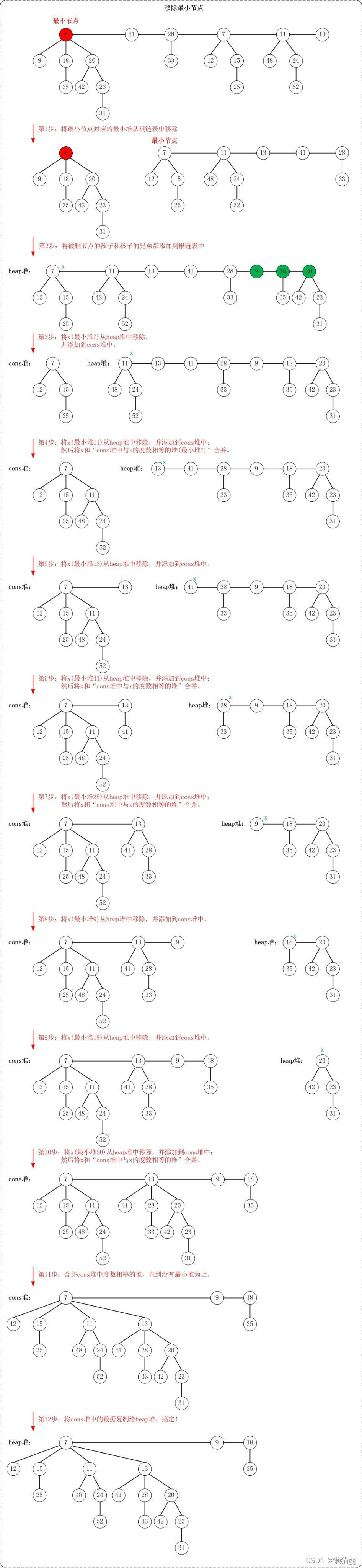
Fib-Heap-Extract-Min(H)z = H.minif z != NILfor each child x of zadd x to the root list of Hx.p = NILremove z from the root list of Hif z == z.rightH.min = NILelseH.min = z.rightConsolidate(H)H.n = H.n - 1return zConsolidate(H)let A[0..D(H.n)] be a new arrayfor i = 0 to D(H.n)A[i] = NILfor each node w in the root list of Hx = wd = x.degreewhile A[d] != NILy = A[d]    // another node with the same degree as xif x.key > y.keyexchange x with yFib-Heap-Link(H, y, x)A[d] = NILd = d + 1A[d] = xH.min = NILfor i = 0 to D(H.n)if A[i] != NILif H.min == NILcreate a root list for H containing just A[i]H.min = A[i]elseinsert A[i] into H's root listif A[i].key < H.min.keyH.min = A[i]Fib-Heap-Link(H, y, x)remove y from the root list of Hmake y a child of x, incrementing x.degreey.mark = FALSE

练习

2-1 给出 19-4(m)中的斐波那契堆调用FIB-HEAP-EXTRACT-MIN后得到的斐波那契堆

1. 7的子树到根列表中
2. 合并相同degree的树
   

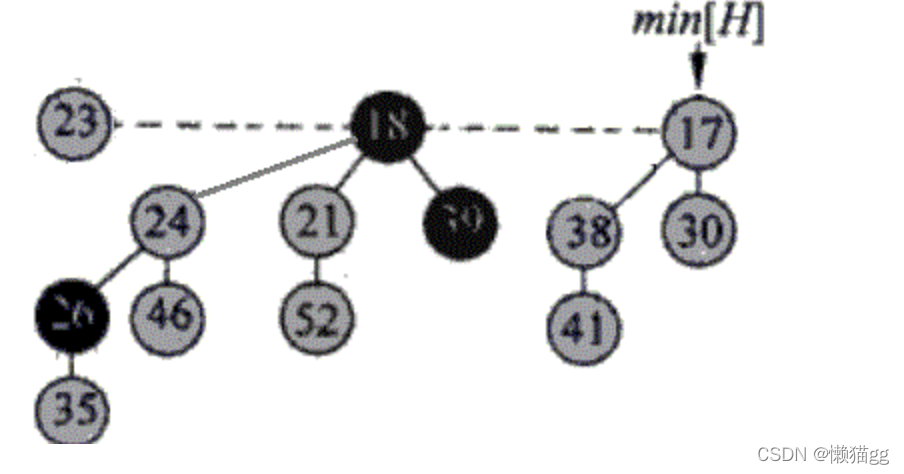
关键字减值和删除一个结点

关键字减值

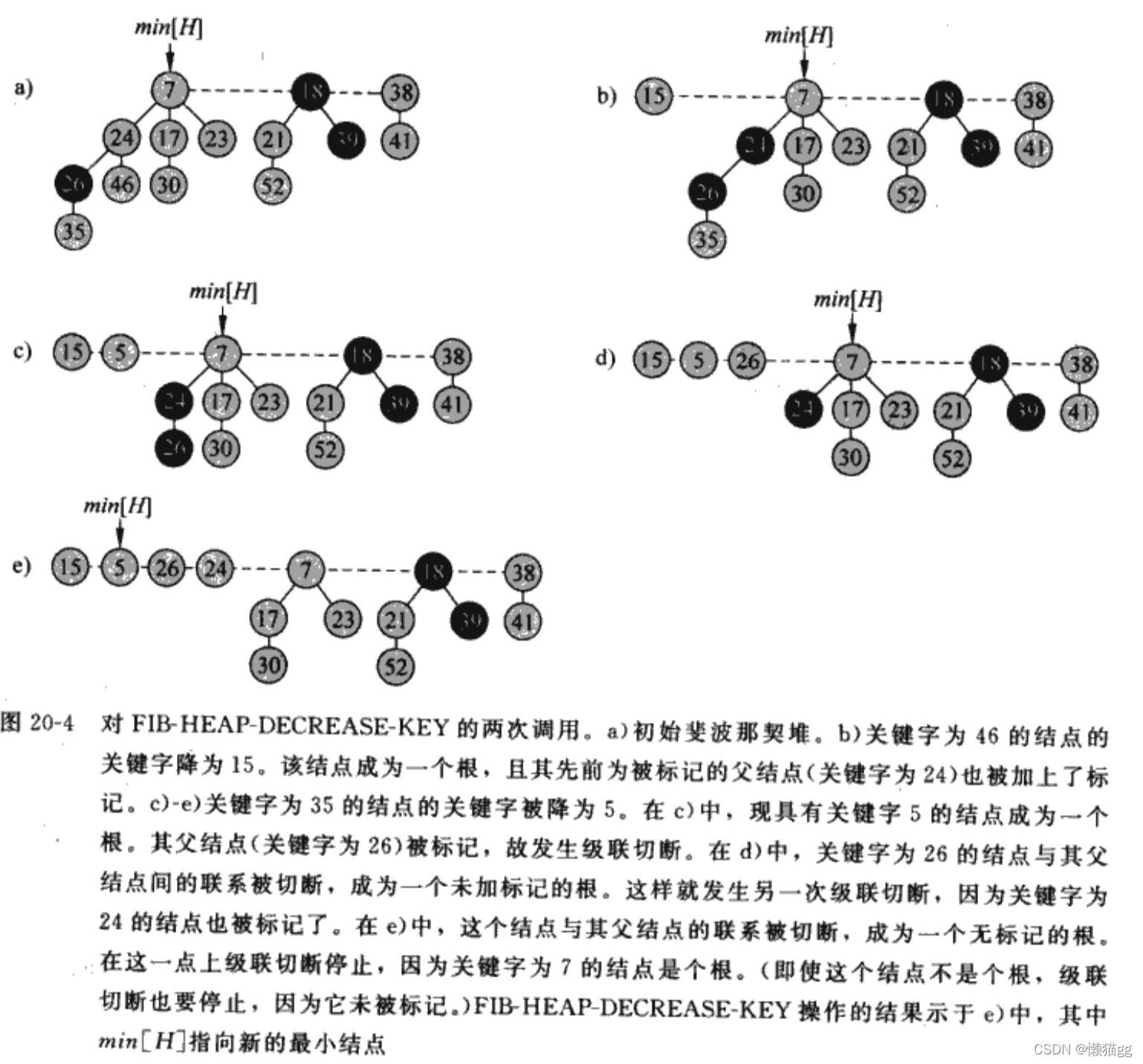
• 首先，将"被减小节点"从"它所在的最小堆"剥离出来；然后将"该节点"关联到"根链表"中。 倘若被减小的节点不是单独一个节点，而是包含子树的树根。则是将以"被减小节点"为根的子树从"最小堆"中剥离出来，然后将该树关联到根链表中。
• 接着，对"被减少节点"的原父节点进行"级联剪切"。
• 最后，别忘了对根链表的最小节点进行更新。

所谓"级联剪切"，就是在被减小节点破坏了最小堆性质，并被切下来之后；再从"它的父节点"进行递归级联剪切操作。
级联操作的具体动作则是：若父节点(被减小节点的父节点)的marked标记为false（默认为false），则将其设为true，然后退出。若为true，将父节点从最小堆中切下来(方式和"切被减小节点的方式"一样)；然后递归对祖父节点进行"级联剪切"。
marked标记的作用就是用来标记"该节点的子节点是否有被删除过"，它的作用是来实现级联剪切。而级联剪切的真正目的是为了防止"最小堆"由二叉树演化成链表。

Fib-Heap-Decrease-Key(H, x, k)if k > x.keyerror "new key is greater than current key"x.key = ky = x.pif y != NIL and x.key < y.keyCut(H, x, y)Cascading-Cut(H, y)if x.key < H.min.keyH.min = xCut(H, x, y)remove x from the child list of y, decrementing y.degreeadd x to the root list of Hx.p = NILx.mark = FALSECascading-Cut(H, y)z = y.pif z != NILif y.mark = FALSEy.makr = TRUEelseCut(H, y, z)Cascading-Cut(H, z)

删除一个结点

1. 先将被删除节点的键值减少。减少后的值要比"原最小节点的值"即可。
2. 取出最小节点即可。

Fib-Heap-Delete(H, x)Fib-Heap-Decrease-Key(H, x, -∞)Fib-Heap-Extract-Min(H)

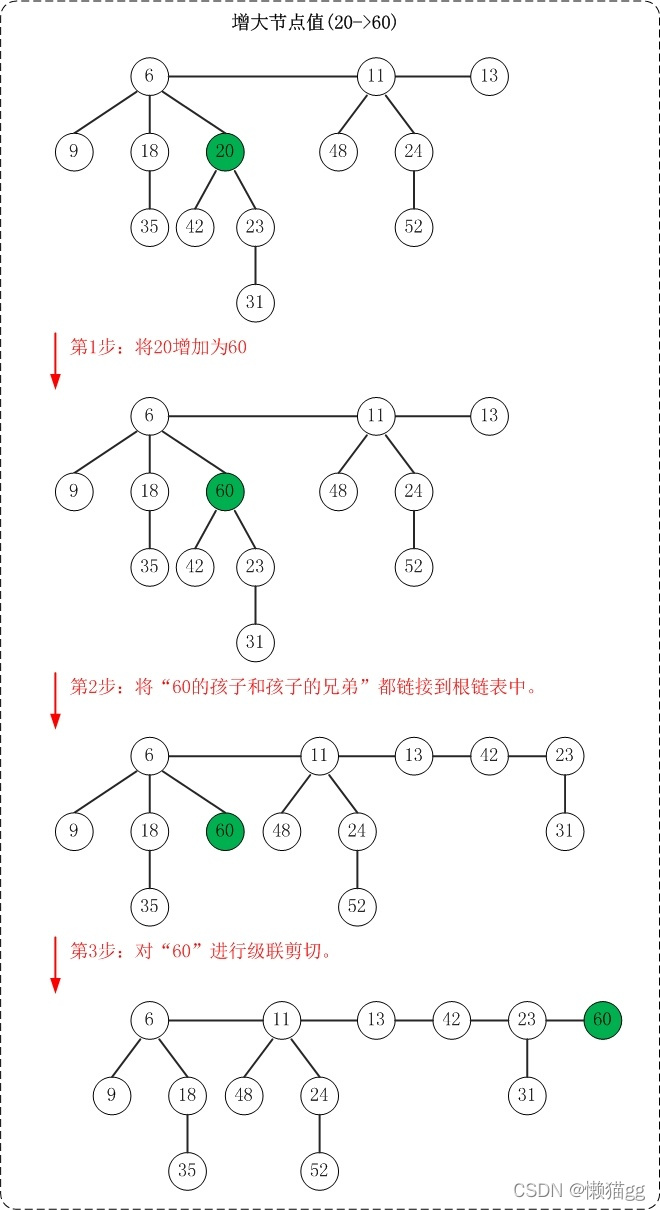
增加关键字值

1. 将增值节点的所有孩子放到根链表中
2. 将增值节点放到根链表中，然后级联剪切

主要参考

《二项堆》
《斐波那契堆》
《斐波那契堆（一）：起源》
《算法导论读书笔记（19）斐波那契堆》
《Fibonacci Heaps》