金融数据分析实验四金融风险价值计算

article/2025/8/29 11:47:10

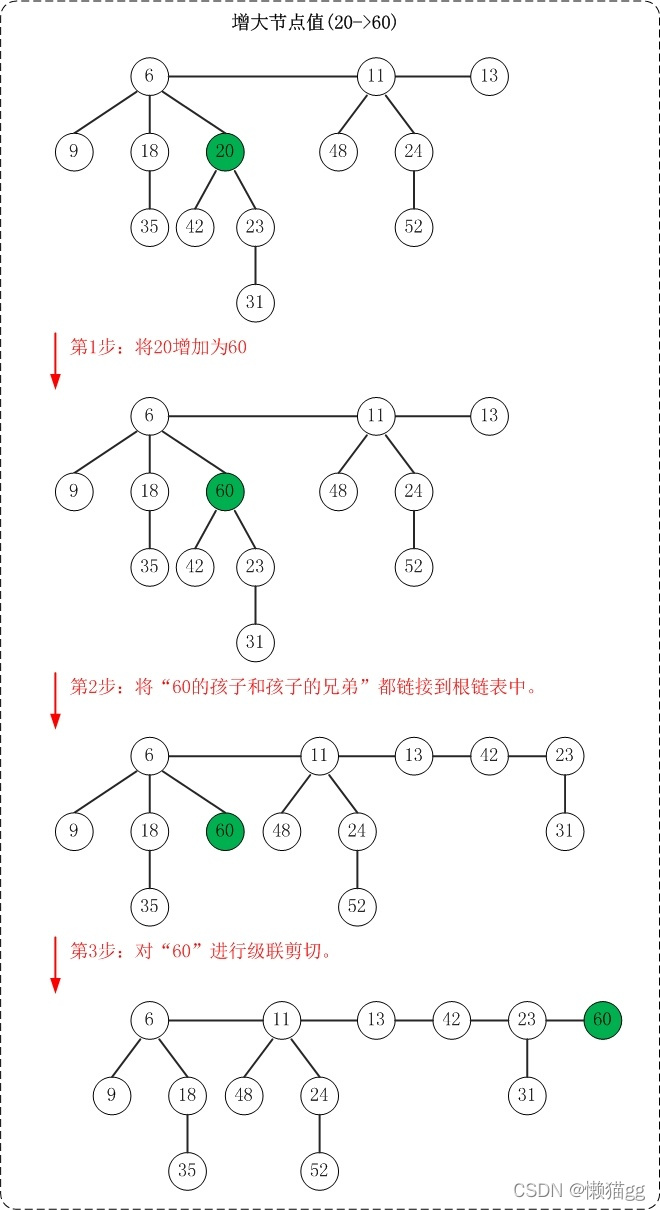
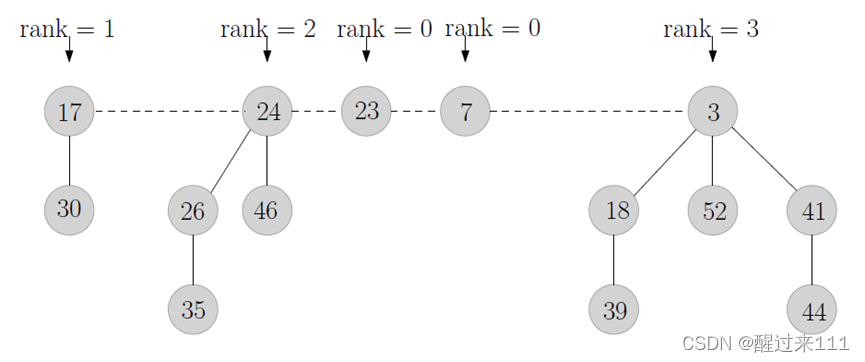
实验原理

VaR的定义：在正常的市场条件下，给定置信水平和持有期，某种投资组合可能发生的最大损失值。
VaR模型不仅描述了损失的大小，还描述了发生损失的概率。
VaR的数学定义：给定置信水平 1 - α 和时间间隔 t ,如果一家实体机构在时间间隔 t 内预计损失额超过M的概率小于α，则称这家实体机构在时间间隔 t 内的VaR为M。
即 P {损失额 > M} < α
VaR的计算是以概率论与数理统计为基础，类似于区间估计
VaR模型可解决的问题：确定内部核心风险资本需求；设定风险限额（建立防洪堤）；在风险调整的基础上更合理地分析业绩；应用于金融监管
对历史数据用不同方法计算样本统计量，计算VaR的方法就不同。主要有三类方法：
一、参数法
1、直接法； 2、移动平均； 3、指数移动平均
二、历史模拟法
1、一般法； 2、拔靴法； 3、改进拔靴法
三、蒙特卡罗模拟法
1、GARCH模型（正态分布、T分布）
2、GJR模型（正态分布、T分布）
3、EGARCH模型（正态分布、T分布）

实验内容

数据：数据从2011/01/04到2012/08/27，共400个样本，取最后50个样本作为回顾测试检验数据，用于对模型进行评价和比较。
在sheet练习题中，C1命名为收益率，在C3中输入=(B3-B2)/B2，并将C3向下拖拽至C401
在这里插入图片描述
一、用直接发计算VaR，写出所有使用的函数、输入、结果等，并画出图。
将sheet练习题复制到新建sheet直接法。

在E2中输入置信水平和α分位数等信息，在H2中输入收益率的均值，在J2中输入收益率的标准差。
在这里插入图片描述
在H3中输入=AVERAGE(C3:C351)求收益率均值，J3中输入=STDEV(C3:C351)求收益率标准差

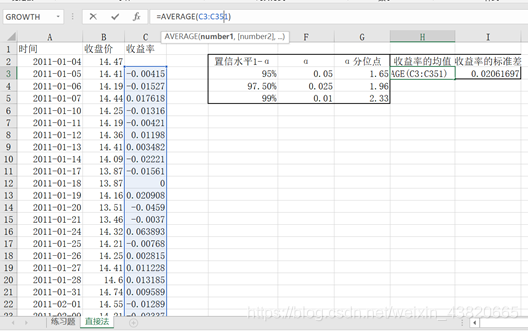
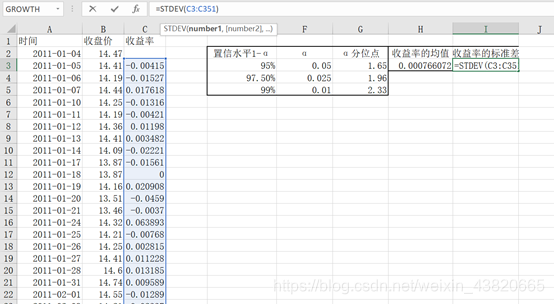
将E2:I5复制，在E345处选择按值粘贴。

在E350、F350、G350中分别输入95%的VaR，97.5%的VaR，99%的VaR，在E351中输入=H346-$G$346*I346，在G351中输入=H346-$G$347*I346，在F351中输入=H346-$G$348*I346。
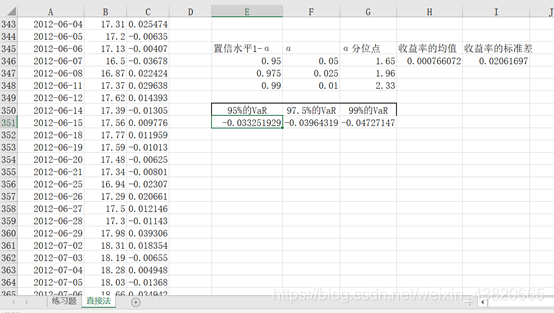
在这里插入图片描述
选中E351复制，在E351按值粘贴。对F351，:G351进行相同的操作。
并将E351:G351拖拽至E351：G401.

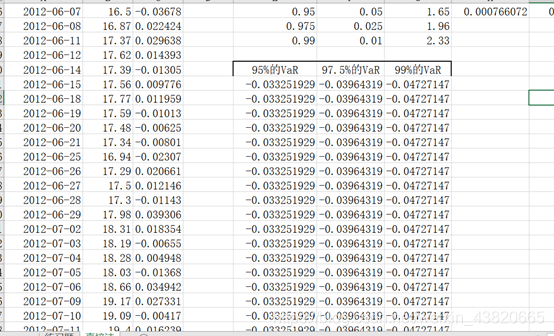
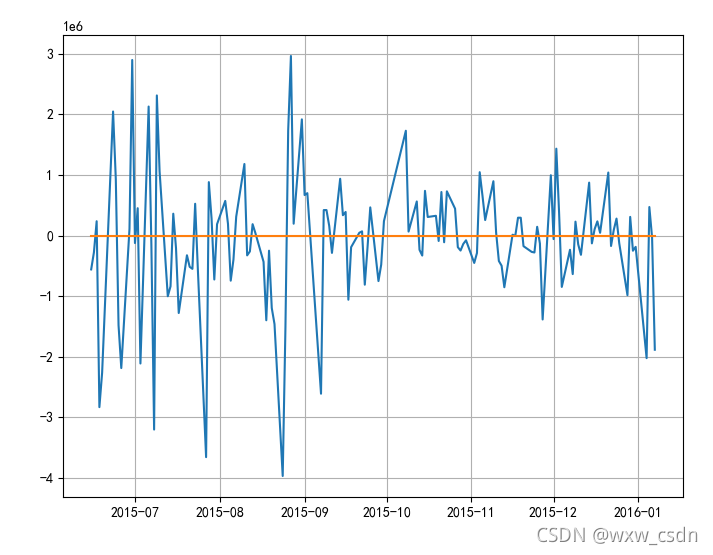
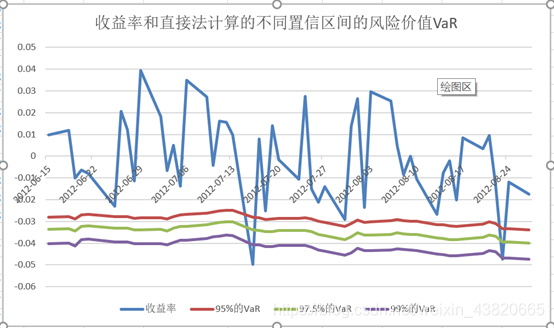
选中A351：A401，C351：C401，E351：G401,绘制折线图。可以看到收益率曲线小于99%的VaR只有两次，根据巴塞尔委员会规定的惩罚区规则来看，属于绿灯区。
在这里插入图片描述
二、用移动平均法计算VaR，写出所有使用的函数、输入、结果等，并画出图。
将sheet练习题复制到新建sheet移动平均法。
取移动平均m为50.E350输入收益率均值，F350输入收益率标准差。E351输入=AVERAGE(C302:C351)，F351输入=STDEV(C302:C351)
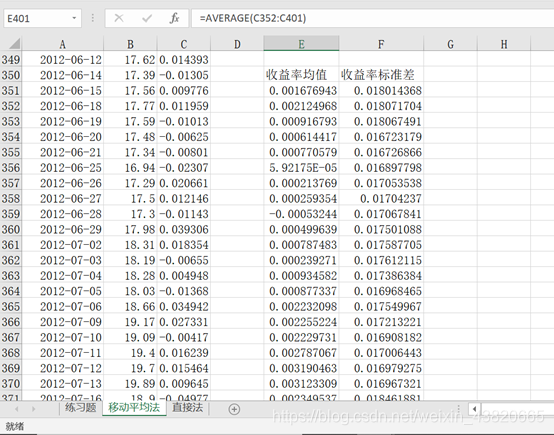
在这里插入图片描述
在E354粘贴置信区间和α分位数表格。在G350、H350、I350输入95%的VaR、97.5%的VaR、99%的VaR.在G351中输入=E351-$G$346*F351，在H351中输入=E351-F351*$G$347，在I351中输入=E351-F351*$G$348。将G351拖拽至G401，将H351拖拽至H401，将I351拖拽至I401。
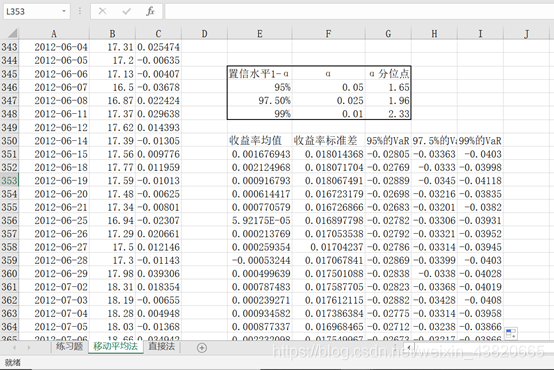
在这里插入图片描述
选中A351：A401，C351：C401，G351：I35，绘制折线图，并修改图例和标题。可以看到收益率曲线小于99%的VaR曲线只有两次，根据巴塞尔委员会规定的惩罚区规则来看，属于绿灯区。

三、用历史模拟法中的一般法计算VaR，写出所有使用的函数、输入、结果等，并画出图。
将sheet练习题复制到新建sheet移动平均法。
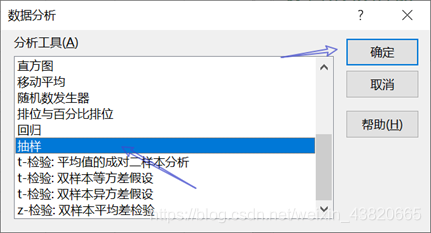
在这里插入图片描述
D1中输入随机样本。点击数据选项卡，点击数据分析，选择抽样，输入区域选择C3：C351，数量为500，输出区域为D2.

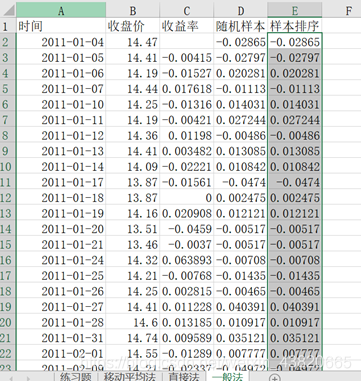
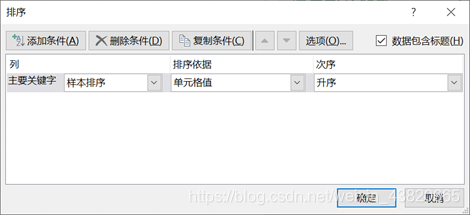
E1中输入样本排序。将D2：D501复制到E2中。选择数据选项卡，点击排序，以当前区域排序。
在这里插入图片描述

点击数据选项卡中的数据分析，选择直方图，输入区域选择E2：E501,输出区域为G2，勾选累积百分率和输出直方图。

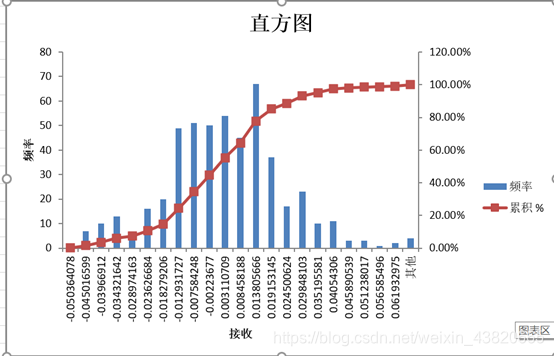
在这里插入图片描述

F351输入95%的VaR，G351输入97.5%的VaR，H351中输入99%的VaR。
95%的VaR：α=5%，在累积列的3.60%和6.20%之间。求算式(6.2%-3.6%)/(13-10)=(5%-3.6%)/x，x=1.61,即找到3.6%对应的接收-0.03967（>=-0.03967），此处是-0.03936,在样本排序中向下数1个就是95%对应的VaR-0.03936。在F352中输入-0.03936，并向下拖拽至F401.
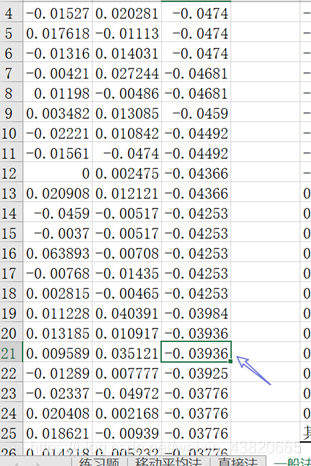
在这里插入图片描述

97.5%的VaR:α=2.5%，在累积列的1.60%和3.60%之间。求算式((3.6%-1.6%))/((10-7))=((2.5%-1.6%))/x，x=1.35,即找到1.6%对应的接收-0.04502（>=-0.04502），此处是-0.044915783,在样本排序中向下数1个就是97.5%对应的VaR-0.04491。在G352中输入-0.04491，并向下拖拽至G401.
在这里插入图片描述
99%的VaR：α=1%，在累积列的0.20%和1.60%之间。求算式((1.6%-0.2%))/((7-1))=((1%-0.2%))/x，x=3.42,即找到1.6%对应的接收-0.05036（>=-0.05036），此处是-0.05036,在样本排序中向下数3个就是99%对应的VaR-0.047399605。在H352中输入-0.04739，并向下拖拽至H401.
在这里插入图片描述

选中A351：A401，C351：C401，G351：I401，绘制折线图，并修改图例和标题。可以看到收益率曲线小于99%的VaR曲线只有两次，根据巴塞尔委员会规定的惩罚区规则来看，属于绿灯区。

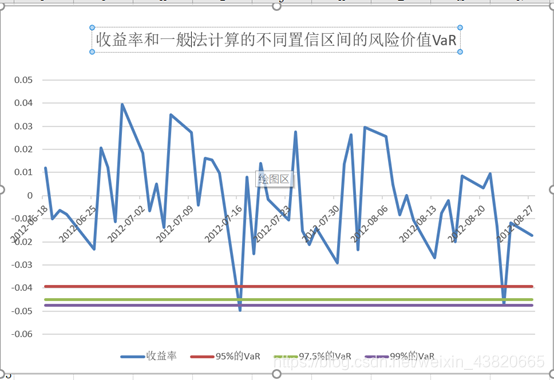
实验心得

VaR的计算可分三步进行：第一步，把资产组合中的每一种资产损益表示为市场因子的函数——市场因子映射；第二步，预测市场因子的波动性——市场因子波动性模型；第三步，根据市场因子的波动性估计资产组合的价值变化和分布——估值模型。在这三步中市场因子波动性模型和估值模型是关键，不同的市场因子波动性模型和估值模型构成计算VaR的不同方法。计算风险价值（VaR）主要有三类：参数方法、历史模拟法和蒙特卡罗模拟法。
参数法假设总体服从某种分布，用历史数据的统计量（如样本均值、样本标准差等）来表示市场因子来计算VaR。参数法主要有直接法、移动平均和指数移动平均三种方法。直接法假设总体服从正态分布，直接计算所有n个样本的样本均值和样本标准差，从而计算风险价值VaR。移动平均法只计算最近m（m称为移动窗口的宽度）个样本的样本均值和样本标准差。指数移动平均是用最近m个样本以指数加权平均来计算样本均值和样本标准差，距离越近的样本的权重越大。
历史模拟法的基本假设是过去的变化情况会在未来重现。利用过去一段时间的历史数据，进行重新抽样，模拟未来一段时间的变化情况，抽样区间和抽样方法的不同，就形成不同的历史模拟法，主要有一般法和拔靴法（Bootstrap）和改进的拔靴法。
蒙特卡罗模拟法假设总体服从某种概率分布，根据历史数据估计其参数，然后利用总体服从的概率分布，模拟未来一段时间的变化情况。
采用回顾测试法对各种模型及模型参数进行评价和比较。可以选出针对特定市场、特定产品在一定时间范围内较为适合的模型和合适的参数。

今天十足抑郁了，坏运气纷至沓来，5555，明天和狗榕出去玩快乐一下。庆庆和曹都有安慰我好感动。好期待去省博呀！明早一定要起来晨刷！