1、VaR简介

2、VaR原理

3、不同VaR实现方法及适用场景

3.1 历史模拟法

3.1.1 使用TUSHARE读入美的复权后估计数据

隆重介绍一下TUSHARE，非常好的财经数据库，能获取到国内股价信息

#环境&数据准备
import sys as sy
import numpy as np
import pandas as pd
import tushare as ts
import pyecharts as pye
from sklearn import datasets as ds
import matplotlib as mpl
from matplotlib import pyplot as plt
import seaborn as sns
import pyecharts as pye#读入美的“000333”2017-01-01 到 2018-11-08复权后数据
df = ts.get_h_data('000333', start='2017-01-01', end='2018-11-8')

计算计算每天的收益率，并展示前条数据样例

#计算日均收益率
df1 = df['close'].sort_index(ascending=True)
df1 = pd.DataFrame(df1)
df1['date'] = df1.index
df1['date'] = df1[['date']].astype(str)
df1["rev"]= df1.close.diff(1)
df1["last_close"]= df1.close.shift(1)
df1["rev_rate"]= df1["rev"]/df1["last_close"]
df1 = df1.dropna()
print(df1.head(10))

打印程序输出：

           close        date   rev  last_close  rev_rate
date                                                     
2017-01-04  28.34  2017-01-04  0.68       27.66  0.024584
2017-01-05  28.21  2017-01-05 -0.13       28.34 -0.004587
2017-01-06  27.92  2017-01-06 -0.29       28.21 -0.010280
2017-01-09  27.79  2017-01-09 -0.13       27.92 -0.004656
2017-01-10  27.72  2017-01-10 -0.07       27.79 -0.002519
2017-01-11  27.17  2017-01-11 -0.55       27.72 -0.019841
2017-01-12  26.79  2017-01-12 -0.38       27.17 -0.013986
2017-01-13  26.81  2017-01-13  0.02       26.79  0.000747
2017-01-16  26.84  2017-01-16  0.03       26.81  0.001119
2017-01-17  27.47  2017-01-17  0.63       26.84  0.023472

使用Pyecharts展示股价走势（Pyecharts非常漂亮的话题工具，擅长于交换展示，不擅长数据探索）

#使用PYECHARTS，画出收盘价曲线
line = pye.Line(title="Mytest")
attr = df1["date"]
v1 = df1["close"]
line.add("000333", attr, v1, mark_point=["average"])
line.render()
line

打印美的000333估计走势

展示美的000333每天收益率对于的密度函数

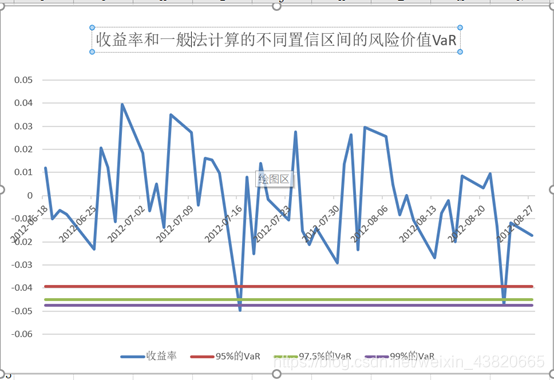
对收益率从小到大排序，根据所选定的置信度，取相应的分位数，作为VaR损失率：

本例中选定如下置信度：

99% - 对应1分位

95% - 对应5分位

90% - 对应10分位

p.s: Numpy 的percentile函数，能直接返回序列相应的分位数

sRate = df1["rev_rate"].sort_values(ascending=True)
p = np.percentile(sRate, (1, 5, 10), interpolation='midpoint')
print(p)

打印程序返回结果（1分位，5分位，10分位）：

[-0.05152336 -0.02971679 -0.0244671 ]

历史模拟法从上面的计算过程来看似乎很简单，细心的你可能已经发现上述计算过程的缺陷，没有使用持有期Tn; 其实本例在计算收益率时使用T1 - T0的计算方法，隐含着持有期为一天的VaR值；如果有计算持有期为100天的VaR值，需要用T100 - T0计算收益率，也就是差分为100阶；相信这里大家能看发现历史模拟法的缺陷了，它不单要假设历史很长一段时间具备独立同分布统计条件，实际上外部因素不可能长期保持不变的分布概率；还有就是持有期较长的话，差分处理导致损失大量数据，这样对数据样本的要求就比较苛刻了。

3.2 方差-协方差法

假定不管是过去的收益率R还是未来的收益率R，都是独立同分布的。所以方差—协方差法借助历史数据来估计未来收益率R的分布。而且，方差—协方差法事先假定R服从某一具体分布，如正态分布;但是该分布函数的所有参数还是未知的，如，正态分布的均值μ，方差σ2。假如现在我们收集了n个收益率R的数据：Ri，i=1,2，…，ni=1,2，…，n，那么我们可用这些历史数据来估计参数。通过参数估计，我们获得了R的概率密度函数f（x）和分布函数F（x）。根据R∗的定义（置信水平p下，未来持有期T的最小收益率），用数学语言表示如下：

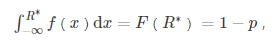
则我们要找的R∗等于：R的概率分布的下分位数Z1−p, 如下图的白色部分；特殊分布可通过查表求得该下分位数Z1−p，

数学公式可表示：（R* - μ）/σ = Z1−p

e.g 标准正态分布下的概率密度图：

对分位值不理解可以看：https://blog.csdn.net/lanchunhui/article/details/80381367

参考案例：
基金A的期初价值为V0=1000万万，假定其服从正态分布，根据收集到的历史收益率（持有期为10天），估计出RR~N（0.1,0.04），假定置信水平p=p=99%，求VaR。其实该题等价于求解正太分布X-N(u, σ2)曲线下，覆盖面值99%所对应的分位数（Z-Score）, 可把非标准正态分布转换成正太分布（x-u）/σ.

计算结果表明：在未来10天，期初价值为1000万的基金A的绝对损失大于366万的概率不超过1%。

3.3 使-协方差法计算美的VaR

使用协方差法计算美的000333，未来持有期为一天的的VaR

from scipy.stats import norm
u = df1.rev_rate.mean()
σ2 = df1.rev_rate.var()
σ  = df1.rev_rate.std()
Z_01 = -norm.ppf(0.99)
#因为(R* - u)/σ = Z_01
#所有R* = Z_01*σ - u
print(Z_01*σ - u)