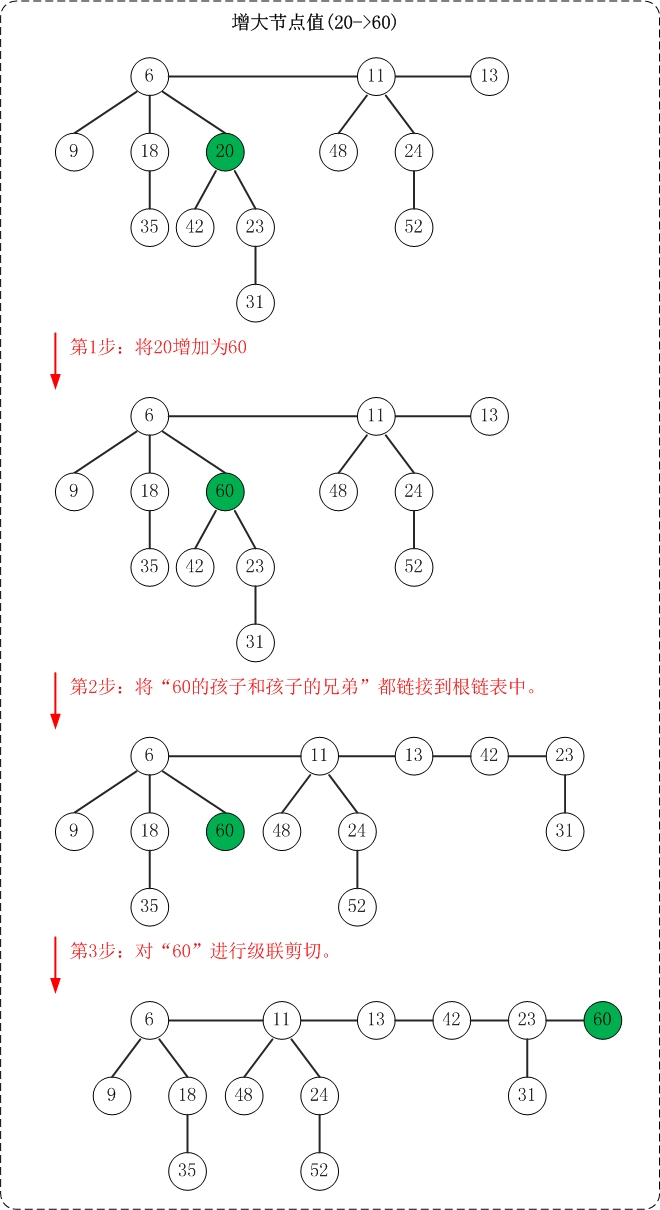
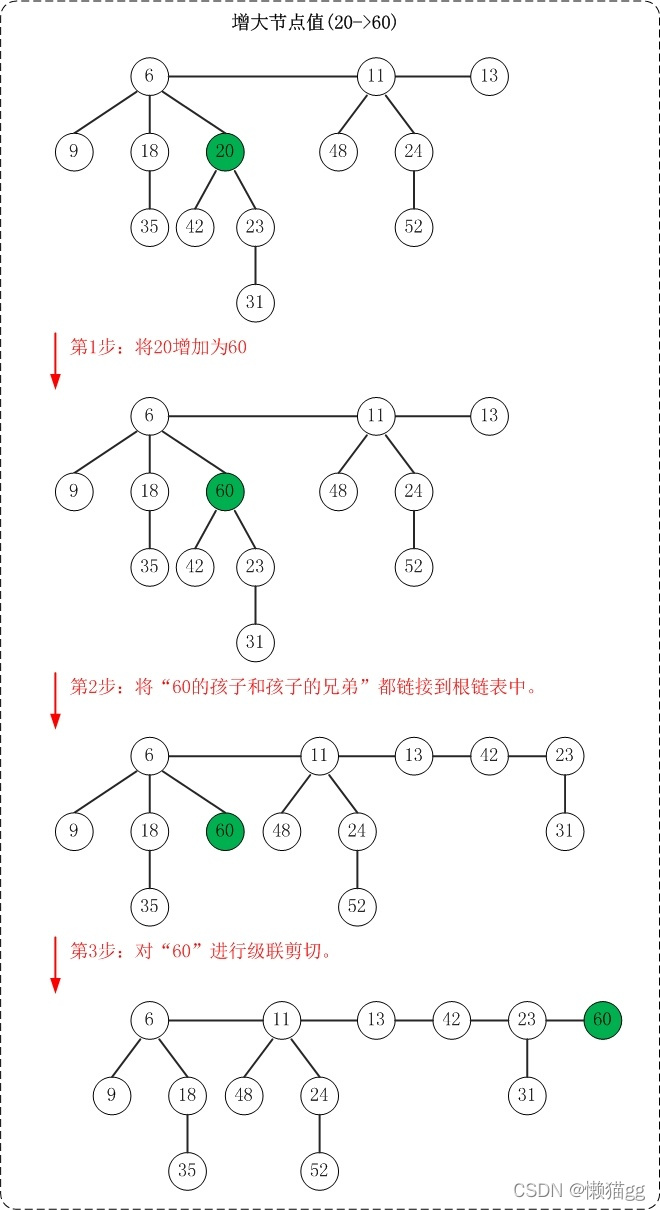
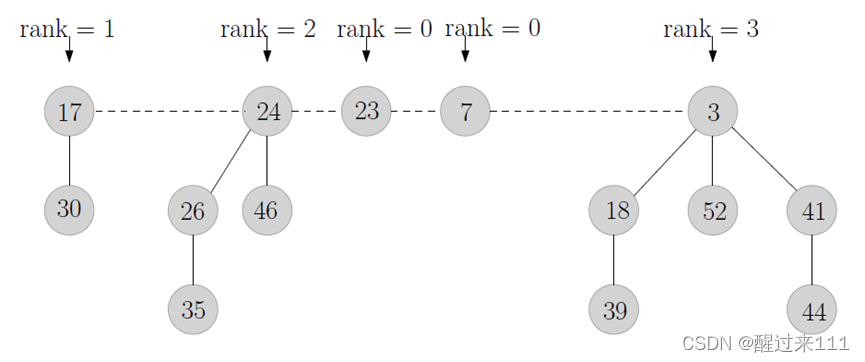
最近我们被客户要求撰写关于风险价值的研究报告,包括一些图形和统计输出。
Python计算获得多资产投资组合的风险度量。
视频:风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例
风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例
,时长10:03
关键概念
- 随着价格的变动,投资经理所持有的市场价值也会发生变化。后者就是所谓的市场风险,衡量它的最流行的方法之一是定义为风险价值。风险本身被看作是实际收益和期望收益之间的差异,两者可能不同。如果它们相等,投资被认为是无风险的。同时,它不能有违约风险,也不能有再投资风险。请注意,期望收益不是投资者认为他们将获得的收益,而是反映了所有经济情况下所有可能结果的平均值。
- 风险价值(VaR)告诉你在一个给定的时间段内,在预先确定的置信水平下,你能损失多少钱。典型的置信度是95%和99%,意味着分析师有95%或99%的信心,损失不会超过这个数字,即5%(或1%)的VaR反映了5%(或1%)最坏情况下的未来最佳收益率。风险值是一个最先进的衡量标准,因为它可以为所有类型的资产进行计算,并考虑到多样化的因素。然而,风险值并不是一个最大的损失数字,所以分析师可能会遇到大于风险值的损失。
- 关于历史序列的假设:
- 过去的收益率是未来收益率的预测指标,但不能保证历史记录会显示未来最坏和最好的情况,但我们用几何平均法将价格转化为收益,所以我们对所有不同的周/月/...收益给予同等的权重,来获得T年内投资收益的复合最终价值。
- 如果资产价格中的期望收益是合理的,那么实际收益率应该围绕这些预期呈正态分布。当收益率可以很好地接近于正态分布时,投资管理就变得更加容易操作了。
定义证明
收益的计算(PT为最终价格,P0为初始价格和股息收益率)。
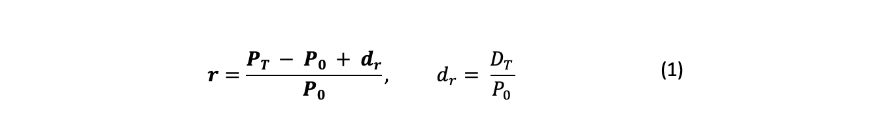
将价格动态转换为收益(2),用几何时间序列(4)计算期望收益(3),而不是算术平均(收益率的波动越大,算术平均和几何平均之间的差异越大)。
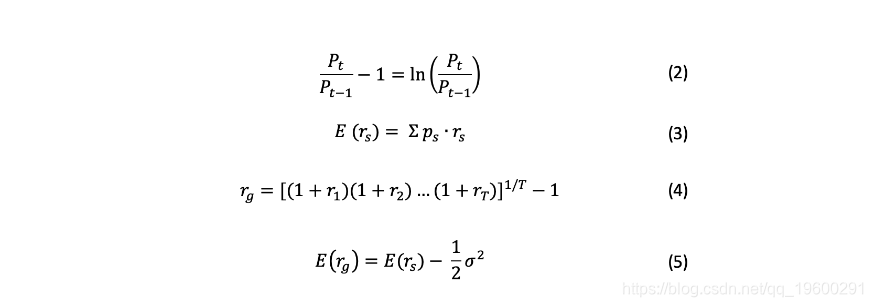
正态分布,以波动率作为风险的衡量标准,即投资的已实现收益的加权平均值的方差的平方根(σ^2),权重等于每种情况的概率ps(6)。
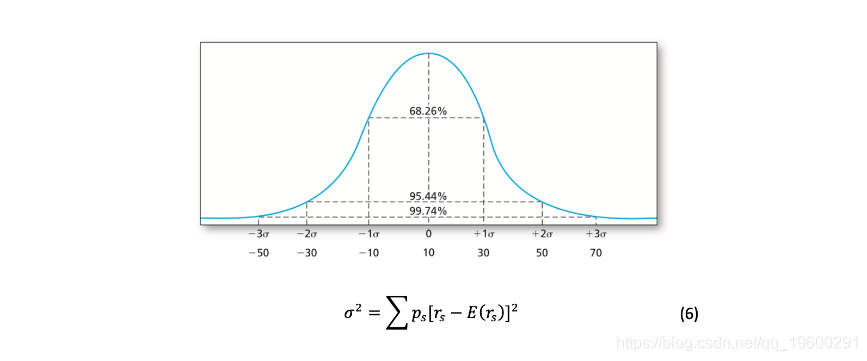
最后,正如 "投资"(Bodie, Kane, Marcus)中所说,VaR是指在给定的时间范围内,收益分布的左尾概率α和右尾概率1-α累积的最小损失额。
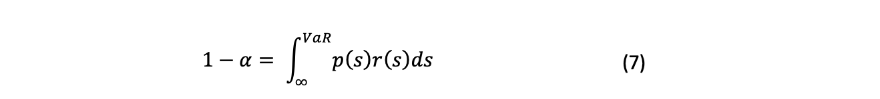
在方差-协方差方法中,我们使用的是参数方法,假设收益是正态分布。因此,我们只需要计算两个参数,即给定收益的平均值和SD(即标准差)。
后者对Excel的计算很有用,我们用Average函数计算收益的平均值,然后STDEV将帮助我们计算标准偏差,最后得出NORMINV将达到VaR计算的目标,VaR(95)和VaR(99)的概率分别为0.05和0.01。
单资产组合VaR
在Python中,单资产组合VaR计算没有那么复杂。
#VaR计算在Python中的应用 #准备工作(每个库都要用 "pip install *libraryname*"来预安装
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt#从雅虎财经下载谷歌数据到定义的时间段内
yf.download('GOOG', '2010-01-01', '2019-01-31')#收益率的计算
df['return'] = Close.pct_change()#VaR计算
VaR_90 = norm.ppf(1-0.9, mean, std_dev)print('VaR 90%置信度: ', VaR_90)
最终输出将是这样的:
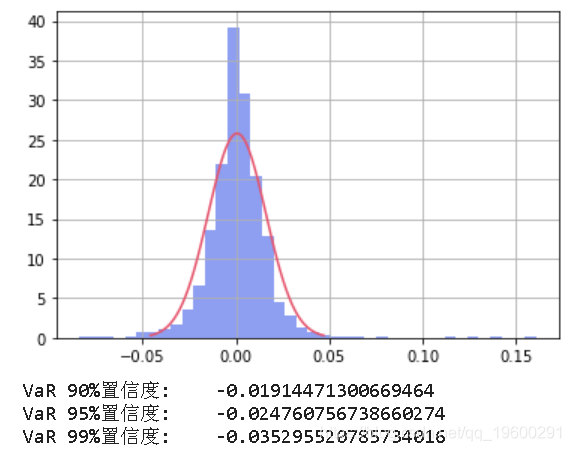
雅虎是一个获得免费金融数据的好方法,另一个途径是Quandl的API库。
为了保持代码结构的连续性,我在下面介绍一个资产类别的样本,以及一个多资产的投资组合结构,其中包括VaR计算。
#准备工作
import numpy as np
import pandas as pd
#从Quandl API导入银行数据(.4表示收盘价)。
ticker = "WIKI/BAC.4"
quandl.get(ticker, #以升序方式呈现数据
sorted( percentage["Close"])print ("99.99%的实际损失不会超过" ,percentile(order_percentage, .01) * 100)
输出以及VaR计算。


多资产投资组合VaR
对于 多资产类别投资组合:
#将数据集扩展到5种不同的资产,将它们组合成一个具有替代风险的投资组合。
[ "WIKI/NKE.4", "WIKI/NFLX.4", "WIKI/AMZN.4"]#收益率的计算
df.pct_change()#不同的风险敞口进入投资组合
percentage * exposures
ptf_percentage = value_ptf['投资组合的价值'] 。
np.percentile(ptf_percentage, .01)print ("99.99%的实际损失不会超过:" round(VaR, 2)print ("预计损失将超过" + (ptf_percentage)) + "超过" ptf_percentage)) + "天数")

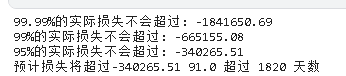
期望损失(Expected Shortfall)
接下来我们讨论另一个基本指标的重要性:期望损失(Expected Shortfall)。
在搜索VAR相关文献时,你会发现有很多关于VAR作为市场风险衡量标准的批评意见。你不可避免地看到期望损失(ES)被提出来作为一种替代。
这两者之间有什么区别呢?
假设我们在99%的置信水平下评估我们的VAR(或者简单地说,潜在的损失),我们将有一系列的损失结果在1%的尾部,
VAR回答了问题:在1%的尾部,整个结果范围内的最小损失是多少?
ES回答了问题:在1%的尾部,整个结果范围内的平均损失是多少?
首先,VaR。
VAR
如果X是h天的收益,那么![]() ,其中
,其中![]() 。例如,对于h=10天的收益,
。例如,对于h=10天的收益,![]() ,我们可以从正态分布中计算出99%的风险值,如下所示
,我们可以从正态分布中计算出99%的风险值,如下所示
h = 10. # 为10天
mu_h = 0.1 # 这是10天内收益率的平均值 - 10%。
sig = 0.3 # 这是一年内收益率的波动 - 30%。VaR_n = normppf(1-alpha)*sig_h - mu_h

以上是参数化的VaR,这意味着我们假设有一定的收益分布。在使用VAR时,通常会使用经验性的VaR,它不假设任何分布形状。在这些情况下,获得VaR只是一个简单的问题,即获得必要的百分数。
条件VaR/期望损失EXPECTED SHORTFALL
考虑到VaR,我们可以通过以下方式定义条件VaR,或CVaR或期望损失。
![]()
对这一点的解释很简单。基本上,它是X的期望值(平均值)。
如果我们再假设一个正态分布,我们可以应用以下公式
![]()
其中![]() 是正态分布,
是正态分布,![]() 是标准正态分布的
是标准正态分布的![]() 四分位数。
四分位数。
接下来是ES。
# 与上述参数相同
alpha**-1 * norm.pdf(norm.ppf(alpha))*sig_h - mu_h
我们不一定要假设正态分布。
上述假设为正态分布,但我们也可以应用学生-T分布。得到等价公式的推导涉及到了这个问题。然而,我们可以通过以下公式计算学生-T分布下的等效风险值
![]()
我们也可以假设一个T分布。
nu = 5 # 自由度,越大,越接近于正态分布
print("99% CVaR ", (CVaR_t*100,2)自由度越大,越接近于正态分布。
# 验证正态分布和Student-t VAR是一样的
nu = 10000000 # 自由度,越大,越接近于正态分布print("99% VaR", round(VaR_t*100,2))

我们可以用实际的市场数据计算出类似的结果。首先,将数据拟合为正态分布和t分布。
mu_norm, sig_norm = norm.fit(returns而各自的VaR和ES可以很容易地计算出来。
绘制具有不同自由度的VaR和CVaR图表
plt.plot(d[0], d[1]*100
plt.plot(np.arange(5, 100), VaR_n*np.ones(95)*100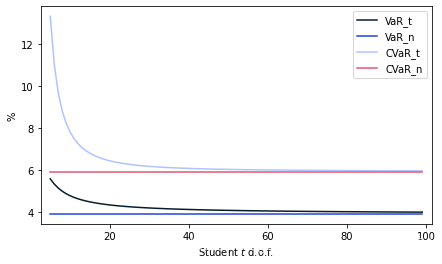
VaR_n = norm.ppf(1-alpha)*sig_norm -munorm
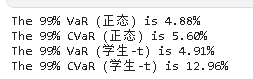
可以很好地了解VaR和ES之间区别的图表如下。
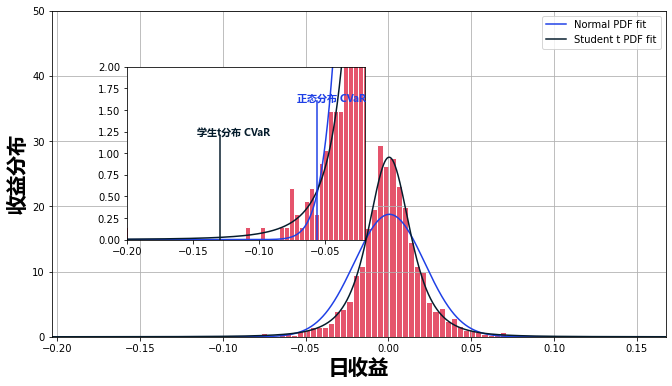
Python确实是一个强大的工具,用于计算和数据可视化。它允许你导入几个不同的预包装库,大大降低了其他代码(如C++)的复杂性。