结构

  斐波那契堆的基础是可合并堆。
数据结构是一个森林。也就是N棵树。这点和二项堆一样。
这个结构没有二项堆那么多的要求。

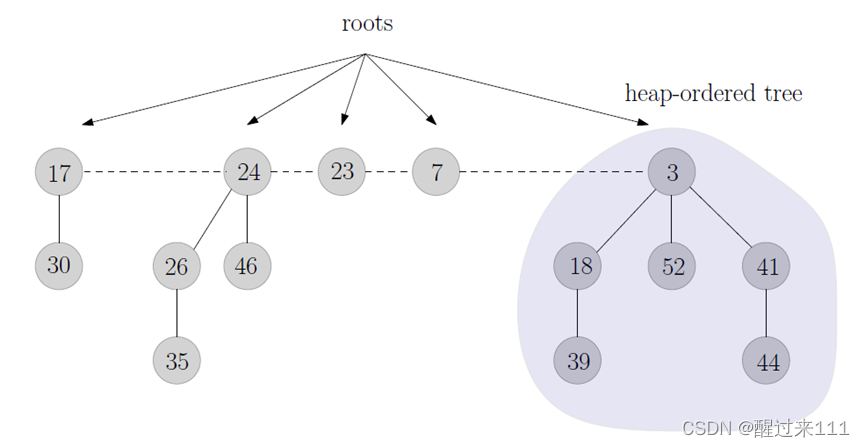
  Rank的概念,是子节点的数目

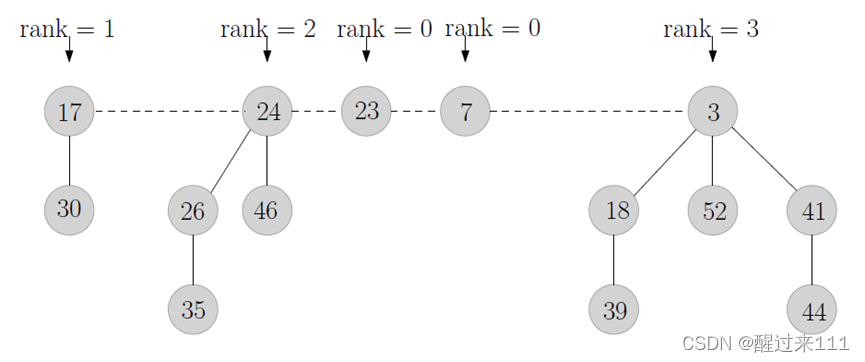
  与二项堆不同的是，斐波那契堆的底层链表要成环，要双向链表。
  而斐波那契堆的节点，是这样的。每个节点有parent，只有一个child。但是每个child都是个双向链表节点。
  所以斐波那契节点实际上是多了两个属性的双向链表节点。所以继承自LinkedListNode。
  斐波那契堆节点主要有以下属性：

# _*_ coding:utf-8 _*_
from com.youngthing.heaps.linked_list_node import LinkedListNodeclass FibonacciNode(LinkedListNode):def __init__(self, key):self.__p = Noneself.__child = Noneself.__rank = 0self.__mark = Falsesuper().__init__(key)@propertydef p(self):return self.__p@p.setterdef p(self, p):self.__p = p@propertydef child(self):return self.__child@child.setterdef child(self, child):self.__child = childif child is not None:child.p = self@propertydef rank(self):return self.__rank@rank.setterdef rank(self, rank):self.__rank = rank@propertydef mark(self):return self.__mark@mark.setterdef mark(self, mark):self.__mark = markdef children(self):x = self.childif x is None:return []result = [x]while x.next is not None and x.next is not self.child:result.append(x.next)x = x.siblingreturn resultdef insert(self, other):"""对于环的插入操作，需要:param other::return:"""def union(self, other):# 连接rootself.next = otherother.next = self.next# 指向新的def __str__(self):return str(self.key)

##插入
  斐波那契堆的插入只不过是在链表上插入一个节点而已。但是这样会有疑惑，这样组成链表，不是查询效率很低吗？
  但是可以斐波那契堆才有了一种lazy的策略，在取最小值的时候才调整，减少链表节点数量。
python代码如下：

def insert(self, key):node: FibonacciNode = FibonacciNode(key)# 连上下一个# 如果是空if self.__min is None:self.__min = node# 只有一个元素的环，要连自己node.next = nodereturn# 环尾end = self.__min.prev# 断开,接上新的end.next = nodenode.next = self.__min# 指向新的if node.key < self.__min.key:self.__min = node

union

  如果是直接合并另一个，代码非常简单

def union(self, other):# 连接rootself.__min.next = other.__minother.__min.next = self.__min.next# 指向新的if other.__min.key < self.__min.key:self.__min = other.__min

##弹出最小
  这个版本比较多。
上海交大的资料里是先consolidate，再删除最小节点。
美国波士顿东北大学的资料是先删除最小节点再consolidate。
但这都不重要，重要的是consolidation过程。
consolidation是斐波那契堆的私有方法，是在删除最小项之前用的。因为斐波那契堆采用了一种懒调整的策略。所以尽量不合并。注意这个合并不是union。核心思想就是把相同rank的节点合并到一起。合并的策略是看谁的key小，key大的就做key小的节点的child，并且和key小者的原有child连起来形成一个环。

def extra_min(self):if self.__min is None:return None# 只有一个元素的时候if self.__min.next is self.__min and self.__min.rank == 0:r = self.__minself.__min = Noneprint('只有一个元素')return rr = self.__min# 继续改代码，先加入进来# 先删除最小,但是要把min的child加进去啊r_child = r.childif r_child is not None:temp = r.nextrchild_end = r_child.prevr.next = r_childrchild_end.next = temp# 移除rr.prev.next = r.nextmin_node = self.find_min_node(r.prev)self.__min = min_nodeself.consolidate()if self.__min.next is None:raise RuntimeError('未成环')r.next = Noner.prev = Nonereturn r

  而调用的方法

# 斐波那契堆的合并
def consolidate(self):# 遍历环寻找等级相等的pair = self.find_pair()while pair is not None:pair[0].link(pair[1])# 为什么会重复两次？pair = self.find_pair()def find_pair(self):start = self.__minwhile start.next is not self.__min:end = start.nextwhile end.next is not start:if start.rank == end.rank:return start, endend = end.nextstart = start.nextreturn None

  核心而且容易出错的方法在FibonacciNode类中，这是两个节点合并为一个节点的方法。

def link(self, other):""":param other: 另一个节点:return: None"""if other.key < self.key:other.link(self)returnprint('link', self, other)# list上移除otherother.prev.next = other.next# 先一个个来# min的变化， list上移除max， child 变成max# max要作为childtemp = self.childself.child = otherself.rank = self.rank + 1# max 的变化,连上min以前的child,但是因为是环，所以需要插进去if temp is not None:temp.prev.next = otherother.next = tempelse:other.next = other#如此，执行完了

这样一个斐波那契堆就写完了。