一、直线方程的三种表示方法
1.一般式：
它实际上表示，直线是两个平面的交线，因此可以由两个平面方程得到，即：

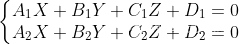
2.点向式（标准方程）：

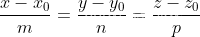
(m, n, p) 为直线方程的方向向量；(x0, y0, z0) 为直线上的一个点。需要注意的是(x-x0, y-y0, z-z0)的方向和方向向量是平行的，也因此推导出了上面的方程。
3.参数方程：

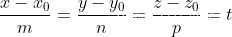
由此就可以得到：

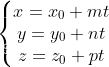
二、三维空间点的直线方程拟合python

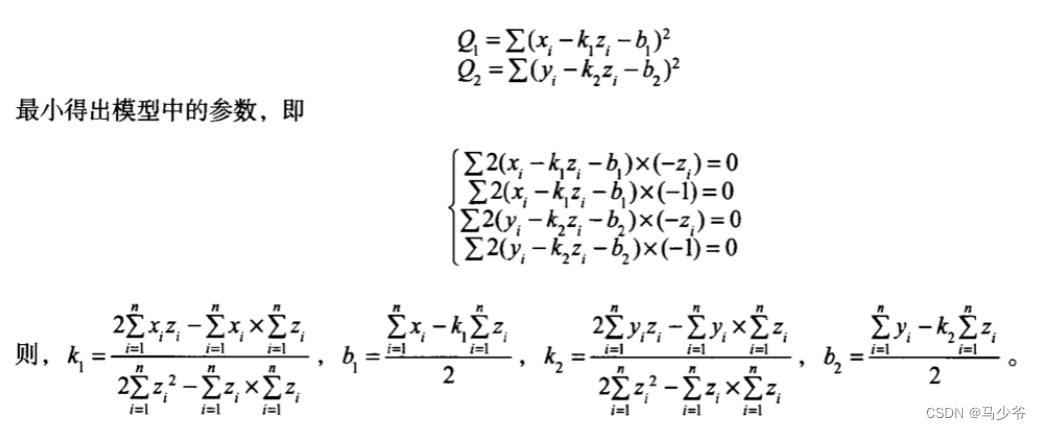
公式中，2应该是n, n表示数据点的个数。

由此我们就可以得到k1, b1, k2, b2。如果想要把它转换成空间直线标准方程，可以先任意取一个z0值，根据k1,b1,k2,b2 就可以求出x0, y0, 然后任意取一个p值，根据k1, k2, 就可以求出m, n值，代入到标准方程即可(所以，标准方程不是唯一的，需要从标准方程的定义去理解为什么不是唯一的)。
python 代码实现：‘

##  由空间3维点拟合出一条直线
def linear_fitting_3D_points(points):'''用直线拟合三维空间数据点。直线方程可以转化成如下形式：x = k1 * z + b1y = k2 * z + b2Input:points    ---   List， 三维空间数据点，例如：[[2,3,48],[4,5,50],[5,7,51]]返回值是公式系数 k1, b1, k2, b2'''#表示矩阵中的值Sum_X=0.0Sum_Y=0.0Sum_Z=0.0Sum_XZ=0.0Sum_YZ=0.0Sum_Z2=0.0for i in range(0,len(points)):xi=points[i][0]yi=points[i][1]zi=points[i][2]Sum_X = Sum_X + xiSum_Y = Sum_Y + yiSum_Z = Sum_Z + ziSum_XZ = Sum_XZ + xi*ziSum_YZ = Sum_YZ + yi*ziSum_Z2 = Sum_Z2 + zi**2n = len(points) # 点数den = n*Sum_Z2 - Sum_Z * Sum_Z # 公式分母k1 = (n*Sum_XZ - Sum_X * Sum_Z)/ denb1 = (Sum_X - k1 * Sum_Z)/nk2 = (n*Sum_YZ - Sum_Y * Sum_Z)/ denb2 = (Sum_Y - k2 * Sum_Z)/nreturn k1, b1, k2, b2

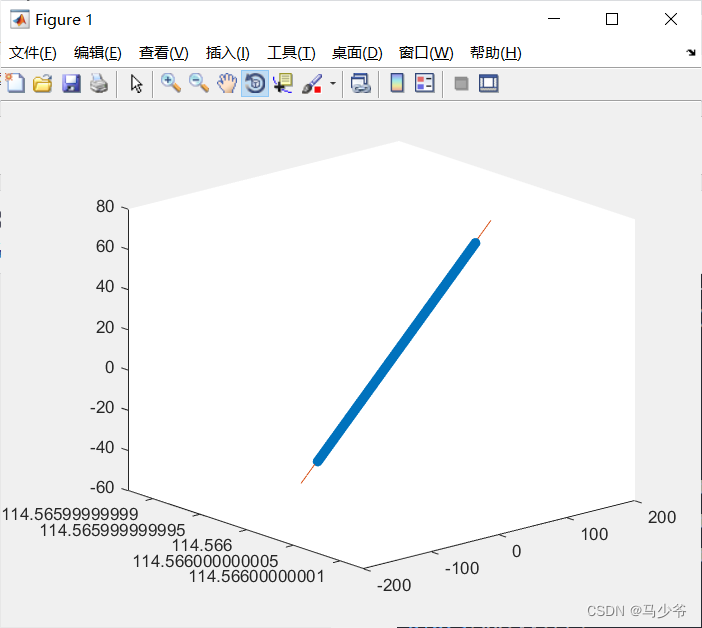
三、三维空间点的直线方程拟合（Matlab）

close all
clear
clchold on
PointV = load('Filletweld.txt');
x = PointV(:,1)
y = PointV(:,2)
z = PointV(:,3)
% figure(1)
% plot3(x,y,z,'r.','MarkerSize',3)
scatter3(x, y, z,'filled')  %散点图函数，'filled'表示画实心点
hold on;    %画了一幅图，再画另一幅图时，原来的图还在，与新图共存
%% 计算平均值（拟合的直线必过所有坐标的算数平均值）
xyz0(1)=mean(x);
xyz0(2)=mean(y);
xyz0(3)=mean(z);%拟合点坐标
%% 奇异值分解计算方向向量(第一种方法)
% 协方差矩阵奇异变换
% 所得直线的方向实际上与最大奇异值对应的奇异向量相同
centeredLine=bsxfun(@minus,PointV,xyz0);
[U,S,V]=svd(centeredLine)
direction=V(:,1)%方向向量%% 画图
t=-150:0.1:150;
xx=xyz0(1)+direction(1)*t;
yy=xyz0(2)+direction(2)*t;
zz=xyz0(3)+direction(3)*t;
%figure(2)
plot3(xx,yy,zz)