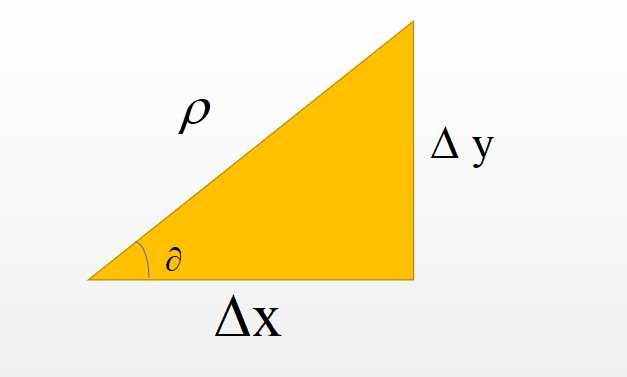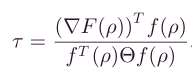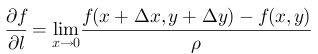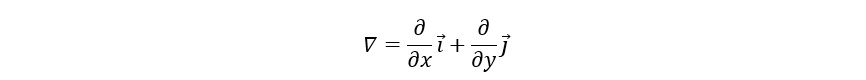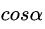全微分的定义

如果函数在区域D内各点处都可微分，那么称这个函数在D内可微分。

以上就是为了解释一下为啥$f(x+\Delta x,y+\Delta y)-f(x,y)=f_x^{{}^{\prime }}$△x + $f_y^{{}^{\prime }}$△y + $\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}$

方向导数与梯度

方向导数

注意：这里的α+β = 90°，即$e_l=(\cos \alpha ,\sin \alpha )$
方向导数要注意：1.函数f(x,y) 2.具体的某一点(x0, y0) 3.$方向e_l$

有了全微分的知识铺垫，很容易看懂
${\frac{\partial f}{\partial l}|}_{\left(x_0,y_0\right)}=f_x\left(x_0,y_0\right)\cos \alpha +f_y\left(x_0,y_0\right)\cos \beta$
又因为α+β = 90°
所以${\frac{\partial f}{\partial l}|}_{\left(x_0,y_0\right)}=f_x\left(x_0,y_0\right)\cos \alpha +f_y\left(x_0,y_0\right)\sin \alpha$

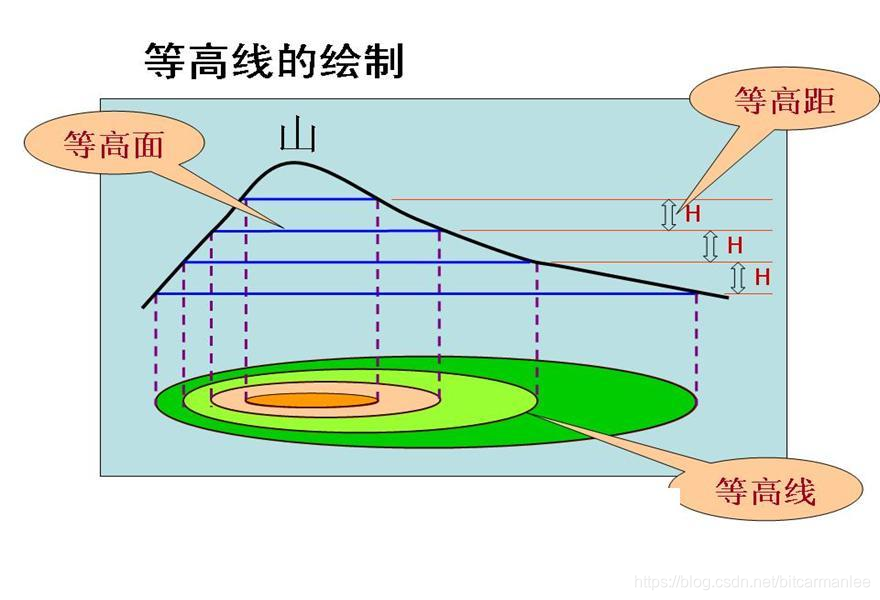
梯度

以上的重点是从方向导数推导到梯度，指出当方向$e_i$与梯度gradf(x0,y0)的方向相同时，函数f(x,y)增加最快。此时函数在这个方向的方向导数达到最大值，这个最大值就是梯度gradf(x0,y0)的模。
即：函数f(x,y)在一点的梯度grad$f$是这样的一个向量，它的方向是函数在这点的方向导数取得最大值的方向，它的模就等于方向导数的最大值。

总结：
方向导数是一个标量，方向导数定义了点 （x,y) 处沿向量 v 方向变化时，对应的函数的瞬时变化率。
方向导数的表达式
${\frac{\partial f}{\partial l}|}_{\left(x_0,y_0\right)}=f_x\left(x_0,y_0\right)\cos \alpha +f_y\left(x_0,y_0\right)\sin \alpha$
$A=\left(f_x(x,y),f_y(x,y)\right),I=(\cos \theta ,\sin \theta )$
${\frac{\partial f}{\partial l}|}_{\left(x_0,y_0\right)}=A\bullet I=|A|\ast |I|\cos \alpha$
(α为方向导数的方向与梯度方向的夹角, α∈[0, 90])
从上面的式子可以推出来，沿着梯度方向的方向导数的值是最大的(就等于梯度的模)，并且大于0(因为梯度的模肯定是正数)，所以当函数沿着这个方向时一定是以最快速度递增的，也就证明了梯度就是函数值增大最快的方向。

参考博客
方向导数的几何意义