原标题：方向导数和梯度是什么？

为什么梯度的方向是函数在该点的方向导数最大的方向，梯度的模是最大方向导数的值？大家在看复习全书时，有认真想过这个问题吗？小编在本文以二元函数为例详细讲解方向导数和梯度，并试图以尽可能通俗地语言回答上述问题。

1.梯度

首先看看二元函数梯度的定义：

如果函数f(x,y)在定义域D内具有一阶连续偏导数，则对于定义域内D每一点P(x0, y0)，都存在如下向量：

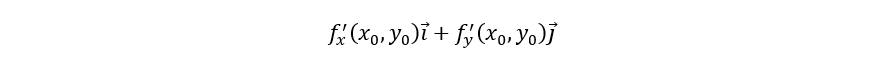
则称上述向量为函数f(x,y)在点P的梯度，记作：

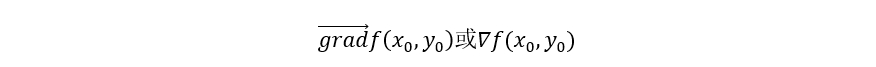
而下面的算子称为向量微分算子或哈密顿算子(nabla算子)：

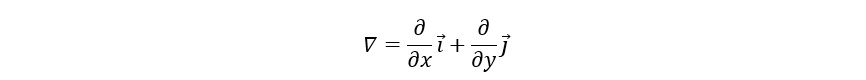
至于为什么在梯度定义中，要附加强要求，即函数f(x, y)在定义域内具有一阶连续偏导数，说实话&