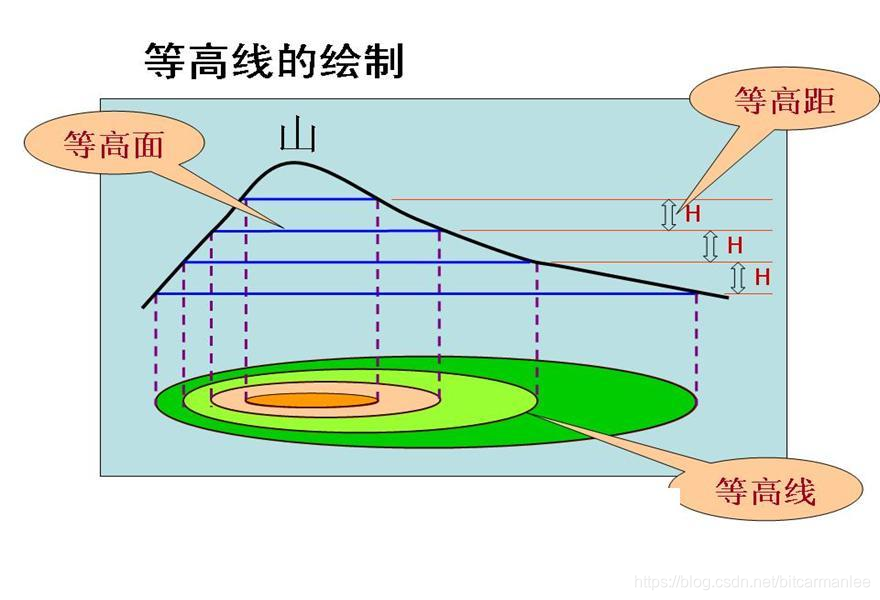
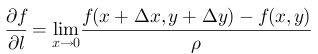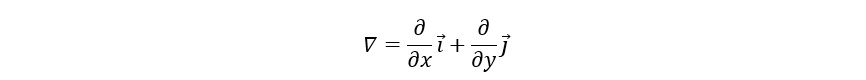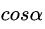梯度方向为何变化率最大

article/2025/9/9 21:47:14

梯度(本质上是一个向量）是机器学习里面的重要基础，借助梯度下降才能最小化损失函数，逐步更新网络参数，得到最佳的函数表示。梯度方向的变化率最大，沿着梯度的反方向，可以最大效率的降低损失函数。在对梯度的理解上，首先明确：先有方向导数的概念，才有梯度的定义

单位向量

以三维空间下为例，单位向量表示为： $(cos \alpha,cos \beta,cos \gamma)$ 。

$\alpha,\beta,\gamma$ 分别是该单位向量与各坐标轴的夹角，通过3个夹角的约束，可以使该向量指向任何方向。且规定是单位向量，其模长为1

角度是表示该单位向量的最重要的部分，直接用 $(\alpha,\beta,\gamma)$ 表示单位向量感觉更直接，用cos表示是为了计算的方便？

方向导数及梯度

以二元函数 $z=f(x,y )$ 为例，在点 $(x_0,y_0)$ 处，求解偏导数时候：

${f_x}'(x_0,y_0)=\frac{\partial f}{\partial x}$ 表示 f 在 x 方向的变化率

${f_y}'(x_0,y_0)=\frac{\partial f}{\partial y}$ 表示 f 在 y 方向的变化率。

但在该点下，可以朝各个方向运动，各个方向都有其各自的变化率，即方向导数。方向导数不能直接求导解出，可通过计算极限来求。

在任意方向上变化的长度，都要对应到各坐标轴上变化了多少，才能找到变化后的点坐标。

规定单位向量 $\vec{l}(cos\alpha,cos\beta)$ ，在此方向上运动 t 个长度，则对应在x,y轴上的运动的长度分别为 $tcos\alpha,tcos\beta$ ，在z方向产生的增量为 $\Delta z=f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0)$ 。

沿着 $\vec{l}$ 方向的变化率为 $\underset{t\rightarrow 0}{lim}\frac{f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0)}{t}={f_x}'(x_0,y_0)cos\alpha+{f_y}'(x_0,y_0)cos\beta$ 。（等式左边是极限表示下的变化率，通过方向导数的定理得出右边式子）