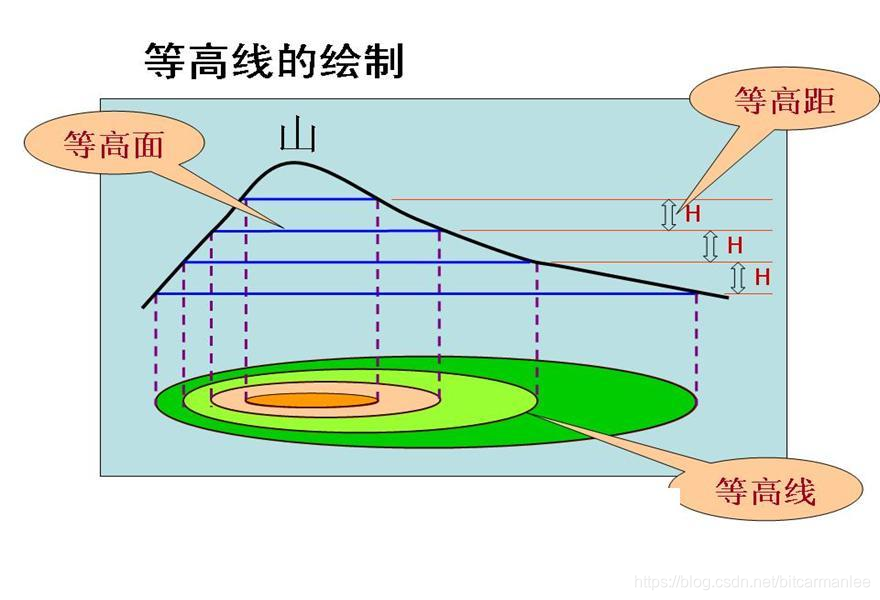
对于梯度下降算法我们熟知的一个例子就是下山问题,当我们位于山的某一点处,沿着当前位置寻找山坡最陡方向以一定步长进行移动,直到走到山脚。那么这个过程具体是怎么做到的?为什么说负梯度方向是下降最快方向呢?
首先我们设定一个初始值【相当于我们在山上的一个初始位置】,优化的目标函数为f(x)【可以理解为将山体轮廓作为目标函数f(x)】,接下来我们可以在
处进行一阶泰勒展开【对函数局部的线性近似】:
我们期望的是在下一个位置处有
【山体的下一个位置的值低于前面的值才说明我们正在下山,这个过程才是有效的】,我们令
则有:
进一步得到:
为了保证可以设
,又为了需要使
距离尽可能的小以减小误差,引入步长系数
,则有:
这里只是举例的一元函数,如果是多元函数,上式为偏导数。根据上述过程不停的迭代寻找最优解。【上述公式也就是我们常看到的权重更新 】
那么又为什么是负梯度方向才是下降的最快方向呢?
首先也是一个向量,这个向量的大小(模值)也其实就是步长系数
【注:步长是一个标量】,如果我们再引入一个单位向量
,那么向量
可表示为:
那么泰勒展开则为:
我们又希望
我们已知是一个为正值的标量,
和
是矢量,两个向量相乘为
,
是两个向量之间的夹角。为了让相乘后的结果为“负最大值”那么向量之间的夹角应为180°,当夹角为0的时候有正的最大值(梯度方向上值增长最快的方向)。所以说当
和梯度方向相反(负梯度方向)的时候,能让值尽可能减小。
我们又已知是单位向量,模为1,则可以表示为:
。于是可得权重更新公式为:
又因为是标量,所以和
写在一起
,如果对于多元函数,则为:
代码实现:
# 假如目标函数为f(x) = 2(x - 5)² # 可以知道当函数值为0的时候,x=5 # 定义函数 def f(x):return 2 * (x - 5) ** 2# 函数求导 def df(x):return 4 * (x - 5)# 定义学习率(步长) learning_rate = 0.1res_x = [] # 保存每次更新后x的值 res_y = [] # 保存每次更新x后y的值x0 = 1 # 初始位置 y = f(x0) # 初始值 y_current = 0 # y当前值# 循环20次 for epoch in range(20):x0 = x0 - learning_rate * df(x0) # 权重更新 梯度下降tmp = f(x0) # 将初始位置先放在一个临时变量中y_current = tmp # 将临时变量中的值赋值为当前值res_x.append(x0) # 记录x的变化res_y.append(y_current) # 记录y的变化
打印一下x的输出结果:可以看出x的值越来越接近于5了
2.6
3.56
4.136
4.4816
4.68896
4.813376
4.8880256
4.93281536
4.959689216
4.9758135296
4.98548811776
4.991292870656
4.9947757223936
4.9968654334361595
4.998119260061696
4.998871556037018
4.999322933622211
4.999593760173327
4.999756256103996
4.999853753662398
print("{:.10f}".format(res_y[-1])) #无限接近0输出为:0.0000000428
可视化:可以看到x的值越来越趋近于5,y的值越来越接近于0

代码参考:梯度下降算法(附代码实现) - 知乎



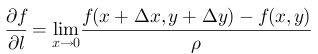



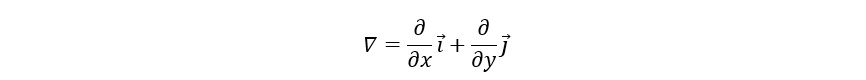

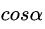







![[字符串]替换空格](https://img-blog.csdnimg.cn/490fdf4bce1c4744ade62df836bb736e.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQWxzb25fQ29kZQ==,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center)